Граничные и начальные условия

Прямыми и косвенными экспериментами показано, что вязкая жидкость “прилипает” к поверхности обтекаемого тела. Силы взаимодействия между поверхностными атомами обтекаемого тела и “прилипающими” к ним молекулами жидкости оказываются достаточными, чтобы последние двигались вместе с поверхностью обтекаемого тела. Поэтому на поверхности тела, обтекаемого вязкой жидкостью, в каждой точке поверхности должны быть равны нулю не только нормальные компоненты скорости жидкости и тела, но также и касательные компоненты. Следовательно, на поверхности обтекаемого тела в каждой точке в общем случае, когда поверхность перемещается со скоростью u, должно выполняться векторное равенство:

. (8.1.7)

Сила, действующая на единицу поверхности тела в направлении 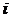- ой координатной оси, определяется компонентами полного тензора напряжений, т.е.

,

где 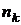есть проекция на ось к внешнего по отношению к телу нормального единичного вектора,

Рассмотрим движение двух несмешивающихся жидкостей. Очевидно, на поверхности раздела этих жидкостей скорости их в каждой точке поверхности раздела должны быть равны, т.е. .

Для любого элемента поверхности раздела двух несмешивающихся жидкостей силы, с которыми жидкости действуют друг на друга, равны по величине и обратные по направлению согласно третьему закону Ньютона. Пусть сила, действующая на жидкость 1 со стороны жидкости 2 на единицу площади в - ом направлении, равна , где есть проекция внешнего по отношению к жидкости 1 нормального единичного вектора на ось к. Аналогично сила, действующая на жидкость 2 со стороны жидкости 1, равна . Очевидно, что . Тогда третий закон Ньютона можно записать в виде:

.

На свободной поверхности жидкости, граничащей с вакуумом, должно выполняться условие

.

Условие (8.1.7) не имеет места при обтекании тел разреженным газом, когда средняя длина свободного пробега молекул газа сравнима с размерами обтекаемого тела. В этом случае вблизи поверхности можно выделить слой толщиной, равной средней длине свободного пробега газовых частиц, в котором частицы не сталкиваются. Внутри этого слоя можно выделить две группы частиц. Одна из них с отрицательной нормальной составляющей скорости каждой частицы имеет некоторую среднюю переносную скорость u₀ вдоль поверхности. Другая часть частиц, отражённых от границы по закону диффузного (равновероятного) рассеяния - закону косинуса имеет нулевую скорость переноса вдоль поверхности. Усреднённая по обеим группам частиц скорость равна u₀ /2. Поэтому тангенциальная скорость газа испытывает скачок вблизи поверхности тела, т. е. газ как бы “скользит” вдоль поверхности. При этом на поверхности тела испытывает скачок и температура. Однако рассмотрение этих явлений не входит в компетенцию механики сплошных сред, а является предметом изучения кинетической теории газов.

В граничные условия входит также задание давления и температуры (или потока тепла) на некоторых поверхностях в жидкости.

Начальные условия необходимы лишь при решении нестационарных задач и заключаются в задании в некоторый начальный момент времени пространственных распределений скоростей, давлений и температур.

8.1.2. Вихревое движение вязкой жидкости

Рассмотрим уравнение движения несжимаемой вязкой жидкости. Пусть массовые силы являются потенциальными, т. е. . Воспользуемся известной формулой векторного анализа для замены 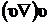в (7.1.1), тогда (8.1.5) можно переписать в виде:

,

.

Применяя операцию ротора к обеим частям уравнения и принимая во внимание, что , , 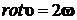получим:

. (8.1.8)

Это уравнение движения для вихря . Если , то из (8.1.8) следует уравнение Громека для баротропного движения идеальной жидкости.

В качестве примера рассмотрим плоский вихрь с компонентами вектора угловой скорости, равными . Частицы жидкости двигаются по окружностям с центром на оси вихря с линейной скоростью . В п.7.4.3 было показано, что для плоского вихря в жидкости 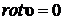. Поэтому второе слагаемое в левой части уравнения (8.1.8) обращается в нуль, и уравнение (8.1.8) имеет место только для 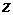- компоненты вектора :

. (8.1.9)

В цилиндрической системе координат уравнение (8.1.9) можно записать в виде:

. (8.1.10)

Уравнение (8.1.10) имеет вид уравнения диффузии и как всякое уравнение параболического типа описывает некоторый необратимый процесс (первая производная по времени).

Пусть в начальный момент времени вихревое движение было стационарным и поддерживалось некоторым постоянным источником (например, вращением тонкого металлического цилиндра). При этом движение в любой точке, кроме оси вихря, как показано в предыдущем разделе (п. 7.4.3), является потенциальным, т.е. 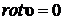. Траектории частиц представляют собой окружности с центром на оси вихря. Линейные скорости частиц находятся из определения циркуляции:

.

Если в начальный момент времени интенсивность (циркуляция скорости) вихревого движения определяется величиной , то в последующие моменты времени решение уравнения (8.1.10) даёт временную зависимость в виде:

(8.1.11)

Правильность решения можно проверить подстановкой (8.1.11) в уравнение (8.1.10).

Из (8.1.11) видно, что интенсивность вихревого движения в центре вихря убывает обратно пропорционально времени. В некоторой фиксированной точке пространства 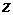- компонента ротора скорости, а следовательно, и интенсивность увеличиваются с течением времени, достигают максимума при , а затем уменьшаются до нуля. При интенсивность вихревого движения в любой точке жидкости стремиться к нулю. Таким образом, в отличие от вихревого движения в идеальной жидкости, которое сохраняется с течением времени, вихревое движение в вязкой жидкости с течением времени захватывает все большие области пространства, занятого жидкостью (диффундирует), и затухает с течением времени вследствие диссипации (рассеяния в пространстве) энергии механического движения из-за вязкости жидкости. В конечном счёте эта энергия механического движения переходит в тепло. После выключения источника вихревого движения в любой точке вязкой жидкости , т.к. , т. е. движение непотенциально во все последующие моменты движения.

Не нашли, что искали? Воспользуйтесь поиском: