Производная сложной функции.

Исследование функции с помощью производной.

Пусть композиция двух функций.

Т.3.1. Если функция дифференцируема по x, а функция дифференцируема по y, то сложная функция дифференцируема по x, причем её производная вычисляется по формуле:

Пример.

Задача. Найти производную сложной функции.

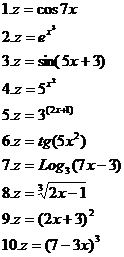
Опр.3.1. Точки мах и min функции называются точками экстремума функции.

Пример. Y=|x|, x=0 – точка min.

Т.3.2. пусть выполняются следующие условия:

1. стационарная точка дифференцируемой функции, т.е. .

2. При переходе аргумента x через точку производная меняет знак,

Тогда точка является точкой экстремума функции , причем:

1) Если при переходе через точку производная меняет знак с «-» на «+», то - точка минимума.

2) Если при переходе через точку производная меняет знак с «+» на «-», то - точка максимума.

Пример.

Опр. 3.2. Функция 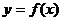называется выпуклой вниз на (a,b), если какова бы ни была точка , график этой функции целиком находится над графиком касательной, проходящей через эту точку.

Аналогично выпуклая вверх с заменой слов «над» графиком на слова «под» графиком.

Опр.3.3. Точка называется точкой перегиба графика функции 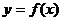, если при переходе через эту точку, функция меняет направление выпуклости.

Т.3.3. Пусть 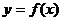дважды дифференцируема на (a,b) и точка является точкой перегиба, тогда .

Пример.

Т.3.4. пусть точка является корнем уравнения , тогда если при переходе через точку вторая производная меняет знак, то точка является точкой перегиба функции 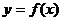, причем:

1) Если при переходе через 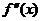меняет знак с «-» на «+», то выпуклость вниз меняется на выпуклость вверх.

2) Если при переходе через 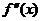меняет знак с «+» на «-», то выпуклость вверх меняется на выпуклость вниз.

Схема исследования функции с помощью производной:

1) найти область определения функции;

2) найти точки разрыва функции и вертикальные асимптоты (если они существуют);

3) исследовать функцию на четность (нечетность) и на периодичность (для тригонометрических функций);

4) найти экстремумы и интервалы монотонности функции;

5) определить интервалы выпуклости (вогнутости) и точки перегиба;

6) исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;

7) найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Исследование функции проводится одновременно с построением ее графика.

Пример. Исследовать функцию и построить ее

график. Решение:

1. Область определения .

2. Функция непрерывна во всей ее области определения. Следовательно, нет ни точек разрыва, ни вертикальных асимптот.

3. Функция четная, так как :

.

График функции симметричен относительно оси ординат.

4. Экстремумы и интервалы монотонности.

. Из уравнения получим три критические точки: 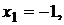. Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).

На интервалах (-∞; -1) и (0; 1) функция убывает, на интервалах (-1; 0) и (1; +∞) - возрастает. При переходе через критические точки x₁ = -1 и х₃ = 1 производная меняет знак с минуса на плюс, следовательно, в этих точках функция имеет минимум. ; .При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум у_max = ƒ(0)=5.

5. Интервалы выпуклости и точки перегиба.

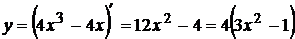. Из уравнения

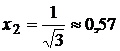получим и . Определяем знак второй производной в каждом из интервалов:

, , .

Таким образом, кривая, вогнутая на интервалах и и выпуклая на интервале , а , - точки перегиба.

;

.

6. Наклонная асимптота имеет вид у = kx + b, если существуют конечные пределы: , ;

.

Таким образом, функция не имеет наклонных асимптот.

7. Дополнительные точки, уточняющие график:

; . Построим график функции:

Задачи.

1. Вычислить производные.

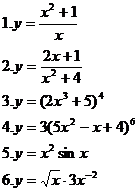
2. Построить график функции.

Не нашли, что искали? Воспользуйтесь поиском: