Решение задач повышенной сложности, тестовых и олимпиадных задач.

Задача 1. (Олимпиада 2002г Карагандинской области, 9 класс)

Хозяйка налила в дырявый бидон керосин. Сколько керосина (в процентах) выливалось из бидона в час, если через два часа в нем осталось на 9% меньше того количества керосина, которое в нем было через час после наполнения?

Решение.

Пусть из дырявого бидона вылилось х% каждый час, а М л керосина было всего в бидоне, тогда через час вылилось:

М л - 100%

У л - х% у = л, а осталось

керосина, за 2 час опять вылилось х% керосина:

л - 100%

Z л – х%

Z= л и осталось в бидоне:

л - 100%

A л – (100 – х) %

А = и это число на 9% меньше, того количества керосина, которое было в бидоне через час после заполнения:

- 100%

- (100-9)%

100

100-х= 0 или 100-х-91= 0

х= 100% (не подходит по смыслу задачи х= 9%

Ответ: 9% керосина из дырявого бидона вылилось каждый час.

Задача 2.. (Олимпиада 2002г Карагандинской области, 10 класс)

Сплавили два сорта чугуна с разным процентным содержанием хрома. Если одного сорта взять в 5 раз больше другого, то процентное содержание хрома в сплаве вдвое превысит процентное содержание хрома в меньшей из сплавляемых частей. Если же взять одинаковое количество обоих сортов, то сплав будет содержать 8% хрома. Определить процентное содержание хрома в каждом сорте чугуна?

Решение. Пусть взяли а кг чугуна, содержащего х% хрома, и а кг чугуна с у% содержания хрома, это значит:

а кг – 100%

Z₁ кг – х%

Z = - количество хрома в чугуне 1 сорта;

Z = - количество хрома в чугуне 2 сорта; количество хрома в сплаве, по условию задачи оно составляет 8%.

2а кг сплава – 100%

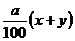кг – 8%

16а =

х +у = 16;

Если же взять одного сорта в 5 раз больше другого, то имеем

5а – 100%

Z - х%

а кг – 100%

Z - у%

Z количество хрома в чугуне 1 сорта

Z количество хрома в чугуне 2 сорта

Z количество хрома в сплаве, его процентное содержание по условию 2у.

Всего сплава 5а + а = 6а (кг)

6а кг - 100 %

Получим систему уравнений

Ответ: первого сорта 11% хрома, а второго сорта 5%.

Задача 3: Двое учащихся – высокий и маленький – вышли одновременно из одного и того же дома в одну школу. Шаг одного из них на 20% короче, чем у другого, но зато он успевал за то же время делать на 20% больше шагов. Кто из них раньше пришел в школу?

Решение: Пусть х м-длина шага высокого мальчика, тогда длина шага маленького 0,8х.

Пусть у - количество шагов в единицу времени высокого мальчика, тогда количество шагов маленького мальчика 1,2у. Поэтому за одно и то же время высокий мальчик прошел ху м, а маленький мальчик (0.8х*1.2у)=0.96ху м. Следовательно, за одно и то же время высокий мальчик проходит большее расстояние. Поэтому его скорость больше, а времени он тратит на один и тот же путь меньше

Задача 4: Заработная плата некоторой категории служащих повышалась два раза, причем процент повышения во второй раз был в два раза меньше, чем в первый. Определите на сколько % повышалась заработная плата в первый раз, если до первого повышения она была равна 7000 р., а после второго – 9240 р.?

Решение: Пусть на х % повысилась з/п в первый раз.

Составим пропорцию:

7000 р.- 100%

у р. – (100+х)%

У= 70(100+х)= 7000+70х – новая зарплата, после первого повышения.

Второй раз повысили на

Составим пропорцию:

7000+70х – 100%

9240 -

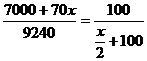
(7000+70х) = 9240

3500х+35х+700000+7000х=924000

35х

35х

х

D = b = 300 =1150600=340

-320 – не подходит по смыслу задачи.

Ответ:20%

Задача 5: Имеются 2 сплава, в первом из которых содержание олова составляет 40%, а во втором – 55%. Сплавив кусок первого сплава со вторым, получили 600 г третьего сплава с содержанием олова 48%. Сколько граммов первого сплава было использовано для получения третьего сплава?

Задание. Решение:

1) 40% 7

48%

55% 8

Пусть = х, тогда .

Составим уравнение, зная, что общая масса этих сплавов 600 г:

7х+8х = 4200

15х = 4200

х= 280

Ответ: 280 г масса первого сплава.

Задача 6: Имеется два образца руды. Один содержит 14 кг железа и 6 кг примесей, другой – 13,5 кг железа и 1,5 кг примесей. Отрезав по куску от каждого сплава и сплавив их, получили 10 кг сплава с процентным содержанием железа 85%. Сколько весил кусок первого сплава?

Решение:

14+6=20(кг) первой руды.

13,5+1,5=15(кг) второй руды.

Составим пропорцию:

20 кг – 100%

14 кг – х%

х = железа в первой руде.

15 – 100%

13,5 – х%

х = железа во второй руде.

70% 5

85%

90% 15

Пусть м - х, тогда м = 10-х

3х=10-х

3х+х=10

4х=10

х=10:4

х = 2,5 (кг) весил кусок первого сплава.

Ответ: 2,5 кг.

Задача 7: Сплав алюминия и магния отличается большой прочностью и пластичностью. Первый такой сплав содержит 5% магния, второй сплав – 3% магния. Масса второго сплава в 4 раза больше, чем масса первого сплава. Эти сплавы сплавили и получили 3 кг нового сплава. Определите, сколько граммов магния содержится в новом сплаве?

Решение: Пусть х кг – масса первого сплава, тогда масса второго сплава 4х кг, 5х – общая масса этих сплавов, по условию она равна 3 кг, или 3000 г.

Составим и решим уравнение:

5х=3000

х=600 (г)

600 (г)

600 г – 100%

у г – 5%

у = (г) магния в первом сплаве.

2400 г – 100%

z г – 3%

z = (г) магния во втором сплаве

72+30=102 (г) магния в новом славе.

Ответ: 102 г.

Задача 8: В смеси кислоты и дистиллированной воды кислоты в 2 раза меньше, чем воды. Когда к этой смеси добавили 300 литров воды, получили смесь с процентным содержанием кислоты 28%. Сколько литров кислоты было в смеси первоначально?

Решение:

Пусть х л - кислоты в смеси, тогда воды 2х л. Всего 3х л.

Составим пропорцию:

3х л – 100%

х л – у%

у % = %

раствор 28

28%

воды 0%

м

1575:3=525 (л) – кислоты.

Ответ: 525 л.

Задача 9: М.В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобрел полхлеба и квас. Хватит ли той же денежки хотя бы на квас, если цены ещё раз вырастут на 20%?

Решение:

Примем денежку за единицу, стоимость хлеба обозначим через х, а стоимость кваса – через у. Составим уравнения: до повышения цен х + у =1, а после повышения 1,2(0,5 х + у)=1. Составим и решим систему уравнений:

Решим второе уравнение 0,6(1- у)+1,2 у =1, получаем, что у = , а затем применяя схему

у (1 + 20 ∙ 0,01)(1 +20∙0,01)

20%

у (1 +20 ∙ 0,01)

20%

у

посчитаем 1,2∙1,2 у= 1,2∙1,2∙ = 0,96 - стоимость кваса после двух повышений цен.

Ответ: денежки хватит на квас.

Задача 10: Цену товара повышали: первый раз на р%, затем новую цену повысили на 2р%. После этого цену товара снизили на 15%. В итоге окончательная цена оказалась выше первоначальной на 12.2%. На сколько процентов была повышена цена товара в первый раз?

Решение:

Пусть исходная цена товара была А.

А₁=А∙(1+р/100) – цена после 1-го повышения

А₂=А₁∙ (1+2р/100)=А(1+р/100)(1+2р/100) – цена после 2-го повышения

0.85∙А(1+р/100)(1+2р/100) – цена после понижения на 15%

В задаче известно, что цена оказалась равной 1,122*А

Уравнение:

0.85∙А(1+р/100)(1+2р/100)=1,122А

(1+р/100)(1+2р/100)=1,32

(1+0.01р)(1+0.02р)=1,32

1+0,03р+0,0001∙2р²-1,32=0

2∙ (0,01р)²+3∙0,1р-0,32=0

Введём замену 0,01р=t

2t²+3t-0,32=0

D=9+4∙2∙0,32=11,56; D=3,4²

t₁=-3+3,4/4=0,4/4=0,1

t₂=-3-3,4/4=-1,6

Обратная замена

0,01р=а1 0,01р=-1.6

р=10% р=-160 – не подходит к условию задачи

Ответ: на 10% повысили в первый раз.

Задача 11: (Олимпиада 2002 г Карагандинской области, 11 класс) Мастер дает сеанс одновременной игры в шахматы на нескольких досках. К концу первых двух часов он выиграл 10% от числа всех играемых, а 8 противников свели вничью свои партии с мастером. За следующие два часа мастер выиграл 10 % партий у оставшихся противников, две партии проиграл, а остальные 7 партий закончил вничью. На скольких досках шла игра?

Пусть всего x партий было сыграно, то есть игра велась на х досках, тогда мастер за первые два часа выиграл 10% этих партий, т. е. (партий). Кроме того он сыграл 8 партий вничью. Значит, за два часа было сыграно партий, а осталось сыграть партий.

За следующие два часа мастер выиграл 10% этих оставшихся партий, т. е.

Составим уравнение:

Ответ: 20 партий было сыграно.

Задача 12: (Олимпиада, посвященная 60-летию Великой Победы, 2005, КГТУ) В колбе имеется раствор поваренной соли. Из колбы в пробирку отливают часть раствора и выпаривают до тех пор, пока процентное содержание соли в пробирке не повысится вдвое. После этого выпаренный раствор выливают обратно в колбу. В результате содержание соли в колбе повышается на 3 %. Определить исходное процентное содержание соли.

Решение: Пусть исходное процентное содержание соли в растворе равно х.

М- весь имеющийся раствор; отливают часть, т.е. М, соли в этом растворе М, остальные (воды)

Теперь часть воды выпаривают, чтобы процентное содержание соли увеличилось вдвое:

соли

y – (100-2x) % воды

y = = = (воды в выпаренном растворе)

всего назад возвращают раствора.

В новом растворе: соли

Общий вес раствора:

Значит,

, разделим на М

;

;

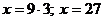
Ответ: 27%исходное процентное содержание соли.

Задача 13: 40 кг раствора соли разлили в 2 сосуда так, что во втором сосуде чистой соли оказалось на 2 кг больше, чем в первом сосуде. Если во второй сосуд добавить 1 кг соли, то количество соли в нем будет в два раза больше, чем в первом сосуде. Найдите массу раствора, находящегося в первом сосуде?

Решение: Пусть х кг чистой соли – в 1 сосуде, тогда во втором – (х+2) кг. Если во второй сосуд добавить 1 кг соли, то количество соли в нем будет (х+3), по условию задачи оно в 2 раза больше, чем в первом.

2 = х+3; 2х-х=3; х=3

3 кг чистой соли в 1 сосуде, тогда во втором сосуде 3+2=5 – кг чистой соли.

3+5=8 кг – чистой соли в 40 кг раствора

Составим пропорцию:

40 кг – 100%

8 кг – х%

х=

20% - соли в растворе.

Составим пропорцию:

3кг – 20%

у кг – 100%

у= кг

15 кг – раствора в первом сосуде.

Ответ: 15кг.

Задача 14: Из сосуда, наполненного кислотой, вылили несколько литров и долили водой; потом опять вылили столько же литров смеси; тогда в сосуде осталось 24 л чистой кислоты. Ёмкость сосуда 54 л. Сколько кислоты вылили в первый раз и во второй?

Решение: Обратим внимание, что на втором шаге воду не доливали.

По условию задачи объем сосуда, наполненного кислотой, 54 л. Её концентрация 100%. Пусть вылили х литров смеси(в первый раз х л кислоты), тогда в сосуде осталось (54-х) литров 100%-ной кислоты. В сосуд доливают х л воды. По определению массовой доли кислоты надо массу кислоты разделить на массу раствора: (54-х)/54.

Опять выливают х литров смеси, в сосуде остается (54-х) л смеси с массовой долей кислоты (54-х)/54.

Чтобы найти массу кислоты в этой оставшейся смеси, надо массу раствора умножить на массовую долю чистой кислоты в этом растворе. По условию масса чистой кислоты в этом растворе стала 24л. Составим и решим уравнение:

(54-Х)∙((54-Х)/54) = 24

(54-Х) = 1296,

зная, что х меньше 54, получим единственное решение х=18

В первый раз вылили 18 литров чистой кислоты. Но во второй раз вылили 18 литров смеси, в ней чистой кислоты было 18*(54-18)/54=12(л)

Ответ: 18л;12л.

Заключение.

Данная тема имеет большое прикладное значение. В школьном курсе математики вводится и изучается процент, потребности учебного процесса требуют, чтобы ученики знали и умели решать простейшие задачи с процентами на уроках химии, физики, биологии, географии. Поэтому повышенное внимание к данной теме оправдано, и требует более глубокого изучения в школьном курсе математики.

Результаты работы можно использовать как:

1. Выполненная работа может быть использована в первую очередь как пропедевтическая, для подготовки учащихся к выпускному и вступительному экзамену в ВУЗы нашей страны

2. Методические комплекты задач трех (основных) типов помогут и учителям, и ученикам при изучении разделов алгебры «Проценты» и «Решение текстовых задач».

3. Результаты работы могут быть использованы на элективных (факультативных) курсах, при самостоятельной подготовке учащихся по данной теме, ведь эта работа способствует изучению рациональных методов решения задач на проценты, не изучаемых в школьном курсе.

4. Приобретенный мною опыт решения задач на проценты делает данную работу актуально-значимой.

В заключение хочется сказать, что умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Поэтому считаю, что моя работа не только найдет практическое применение на уроках алгебры, как пример решения задач разных видов с практическим содержанием, но и поможет увидеть широту возможных приложений математики, понять её роль в современной жизни.

Отзыв

Учащаяся 9 б класса Лукина Юлия выполнила большую исследовательскую работу по изучению вопроса решения задач на проценты, она работала над данной темой в течение года. Юлия проявила большую самостоятельность в отборе материала по теме, при решении задач. В результате она разобрала основные методы решения задач на проценты, применила разобранные методы при решении олимпиадных, тестовых и задач повышенной сложности. Работа, выполненная ученицей, может быть использована как во внеклассной работе, при подготовке учащихся к олимпиадам и конкурсам различного уровня, на факультативах. В результате собран большой материал, который можно включить в элективный курс по решению текстовых задач.

Директор СШ № 3 А. С. Аманбеков

Учитель математики и информатики

Гудовщикова.Д.С.

Средняя школа №3

город Шахтинск

Список литературы:

1. Шевкин А.В. Обучение решению текстовых задач. – М.: ТИД «Русское слово – РС», 2002.

2. Лебедев В.В., Михайлов П.А. Пособие по математике для подготовки к вступительному экзамену. – М.: ГАУ,УЦ «АЗЪ»,1998.

4. Виноградов И.М. Энциклопедия по математике. – М.: том 2, с.168-171.

5. Шабунин М.И. Математика для поступающих в Вузы.- М.: 2000 г

6. Энциклопедия для детей.Т.11. Математика/ Главный ред. М.Д. Аксенова. – М.: Аванта+, 1998.

7. Савицкая Е.В., Серегина С.Ф. Уроки экономики в школе. – М.: Вита-Пресс, 1999.

8. А.В. Спивак Математический праздник. Ч.1 - М.: Бюро Квантум, 2000 (Приложение к журналу «Квант», №2/2000).

9. Захарова А.Е. Несколько задач «про цены». //журнал «Математика в школе».-2002-№8.

10. Седова Е.А. Проценты в X классе общеобразовательного направления. // журнал «Математика в школе».-1994-№4.

11. Е.Т. Астахова и др. Арифметические задачи. Учебное пособие для проведения практикума по решению задач. – Красноярск: Изд-во КГПУ, 1995

12. Балаян Э.Н. Как сдать ЕГЭ по математике на 100 баллов. – Ростов н/Д: изд-во «Феникс», 2004.

13. Г. В. Дорофеев, Е. А. Седова. Процентные вычисления. – М.: Дрофа, 2003 г.

14. А. П. Савин. Для чего нужны проценты // Квант. 1986. №2

15. А. С. Симонов. Проценты и банковские расчеты // Математика в школе. 1998. №4

Не нашли, что искали? Воспользуйтесь поиском: