Закон сохранения электрического заряда 2 страница

Согласно физическому смыслу связь между векторными линиями (концентрические окружности) и (прямые) может быть представлена схематически так, как показано на рисунке.

Возьмем дивергенцию от левой и правой части (1.35)

.

Следовательно,

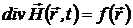, (1.37)

где - произвольная функция координат. Пусть в начальный момент времени заряды двигались так, что магнитное поле носило стационарный характер. Тогда

.

Поскольку = 0 в начальный момент времени, то будет равно нулю в любой другой момент времени. Этот результат отражает опытный факт отсутствия магнитных зарядов (магнитных монополей).

Из выражения (1.37) следует уравнение

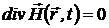(1.38)

или в интегральной форме

= 0. (1.39)

Уравнения (1.38) и (1.39) - последние из системы уравнений Максвелла.

1.1.6. Движущийся точечный заряд в электромагнитном поле. Сила Лоренца.

Распределение зарядов и характер их движения в пространстве не могут быть заданы произвольно. Очевидно, что электромагнитное поле оказывает существенное воздействие на движущиеся заряды, изменяя их распределение в пространстве.

На заряд, движущийся в электромагнитном поле, действует сила

, (1.40)

где - сила, действующая на заряд со стороны электрической составляющей электромагнитного поля, - сила, действующая на заряд со стороны магнитной составляющей электромагнитного поля.

Для нахождения воспользуемся формулой Ампера

, (1.41)

где - сила, действующая на элемент с током . Воспользуемся соотношением 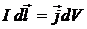. Тогда

, (1.42)

и плотность силы Ампера

. (1.43)

Сила Ампера определяется формулой

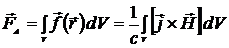. (1.44)

Рассмотрим одиночный электрический заряд q, движущийся со скоростью . Плотность тока этого заряда

.

Тогда из (1.44) с учетом (1.45) получим

= .

Таким образом, на движущийся электрический заряд со стороны магнитной составляющей электромагнитного поля действует сила

, (1.45)

называемая силой Лоренца. Часто силой Лоренца называют полную силу

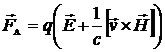, (1.46)

действующую на движущийся заряд со стороны электромагнитного поля.

Уравнения движения системы зарядов в электромагнитном поле:

, (1.47)

где - импульс точечного заряда . Для системы зарядов, находящихся в объеме 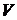, введем полный импульс . Затем перейдем от суммирования по частицам к интегрированию по объему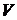

(1.48)

или

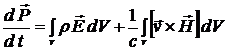. (1.49)

1.1.7. Система уравнений Максвелла-Лоренца.

Запишем систему уравнений, полученных ранее как обобщение опытных законов электромагнетизма. В дифференциальной форме уравнения Максвелла, описывающие электромагнитное поле при заданных распределениях зарядов и токов, имеют вид:

(1.50)

Отметим, что первое уравнение системы (1.50) обобщает закон электромагнитной индукции Фарадея. Второе уравнение отражает факт отсутствия в природе магнитных зарядов. Третье уравнение является обобщением опытного закона Био- Савара – Лапласа. Четвертое уравнение обобщает закон Кулона.

В интегральной форме система уравнений Максвелла

(1.51)

где - полный заряд, а - полный ток.

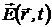Считая заданными функциями и , из системы уравнений Максвелла (1.50) можно однозначно определить шесть неизвестных компонент векторных функций и , которые определяют электромагнитное поле. Всего же в системе уравнений Максвелла (1.50) имеется восемь

скалярных уравнений. Казалось бы, что система этих уравнений - переполнена. Однако, учитывая закон сохранения заряда, можно показать, что второе и четвертое уравнения системы (1.50) есть следствия шести остальных скалярных уравнений.

Рассмотрим третье уравнение из (1.50) и посчитаем

. (1.52)

Из уравнения непрерывности имеем . С учетом этого выражения, из (1.52) получим

,

и

, (1.53)

где - произвольная функция координат. Полагая заряды покоящимися в начальный момент времени, имеем = 0. Но тогда будет равняться нулю и в любой последующий момент времени, т.е. .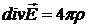

Из первого уравнения системы (1.50) следует

. (1.54)

Таким образом,

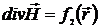, (1.55)

где 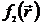- произвольная функция координат. Аналогично считаем, что в начальный момент времени магнитное поле стационарно и значит 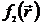= 0. Следовательно, 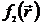= 0 в любой другой момент времени.

a) Система уравнений Максвелла является полной. Это означает, что при заданных начальных и граничных условиях из шести независимых уравнений Максвелла можно однозначно определить шесть неизвестных скалярных функций , определяющих электромагнитное поле.

b) Система уравнений Максвелла представляет систему линейных дифференциальных уравнений в частных производных. Поэтому выполняется принцип суперпозиции. Действительно, если - решение уравнений Максвелла при заданных значениях , то является, в силу линейности уравнений, также решением системы уравнений Максвелла при заданных значениях .

Легко увидеть, что система уравнений Максвелла не противоречит закону сохранения заряда в дифференциальной форме

(1.56)

или в интегральной форме

. (1.57)

В общем случае распределение зарядов и токи нельзя задавать произвольно, так как электромагнитное поле определяет характер движения зарядов. Поэтому необходимо дополнить систему уравнений Максвелла уравнениями движения зарядов

, (1.58)

или

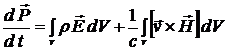. (1.59)

Полную систему уравнений (1.50), (1.56), (1.58) в дифференциальной форме, или (1.51), (1.57), (1.59) в интегральной форме, часто называют системой уравнений Максвелла-Лоренца. Эта система уравнений описывает как электромагнитное поле в вакууме, так и движение электрических зарядов, являющихся единственным источником электромагнитного поля.

Таким образом, имеет смысл говорить об электродинамической системе (электромагнитное поле и электрические заряды), описываемой системой уравнений Максвелла-Лоренца.

2. Закон сохранения энергии в микроскопической электродинамике. Плотность энергии. Вектор Пойнтинга.

За единицу времени (1 с) силы электромагнитного поля совершают работу над заряженными частицами, находящимися в объеме 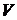, ограниченном поверхностью

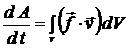, (2.1)

где плотность силы Лоренца

. (2.2)

Тогда

, (2.3)

Так как , то, с учетом , получим

. (2.4)

Из уравнений Максвелла (1.50) следует

,

и поэтому

. (2.5)

В правой части (2.5) добавлено слагаемое

=0,

так как из (1.50) имеем: . Тогда

. (2.6)

Учтем, что

,

.

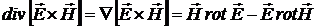Из (2.6) получим

, (2.7)

или

. (2.8)

Введем вектор

,

называемый вектором Пойнтинга, и скаляр

- плотность энергии электромагнитного поля.

Из выражения (2.8), применив теорему Остроградского – Гаусса, получим с учетом введенных выше обозначений:

. (2.8)

Распространим интегрирование на все пространство. При этом и стремятся к нулю при быстрее, чем 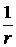. Отсюда следует, что быстрее, чем . Площадь поверхности при растет как . Таким образом, при .Следовательно,

. (2.9)

Смысл последнего выражения очевиден: работа совершается за счет энергии электромагнитного поля. Поэтому - энергия электромагнитного поля и - плотность энергии.

Если рассматривать электромагнитное поле в конечном объеме, то

. (2.10)

Таким образом, убыль энергии электромагнитного поля в конечном объеме 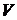связана с работой в единицу времени 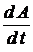над зарядами и потоком

энергии через поверхность . Модуль вектора Пойнтинга имеет смысл плотности потока энергии, т.е. количества электромагнитной энергии, протекающей за единицу времени через единичную площадку. Если в этом объеме отсутствуют электрические заряды, то 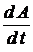= 0 и

. (2.11)

Подставим выражения для энергии в (2.11) и применим теорему Остроградского – Гаусса:

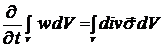. (2.12)

Из-за произвольности выбора объема 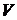получим

. (2.13)

Это уравнение - аналог уравнения непрерывности. Поэтому электромагнитную энергию можно рассматривать как некоторую материальную субстанцию, распределенную в пространстве, и способную вытекать из конечной области пространства.

3. Потенциалы электромагнитного поля. Калибровочная инвариантность. Уравнения для потенциалов при калибровках Лоренца и Кулона.

Рассмотрим уравнения Максвелла

(I) (II) (3.1)

Из второго уравнения системы (II) следует, что напряженность магнитного поля

, (3.2)

где - векторный потенциал электромагнитного поля. Действительно, . Подставим (3.2) в первое уравнение системы (II)

, (3.3)

или

. (3.4)

Таким образом, поле - потенциальное и значит

, (3.5)

где - скалярный потенциал электромагнитного поля. Согласно (3.2) и (3.5) для описания электромагнитного поля вместо напряженностей и можно рассматривать потенциалы и , тем самым уменьшить число неизвестных скалярных функций с шести до четырех. При такой замене система уравнений (II) выполняется автоматически.

Выбор и при заданных и неоднозначен. Действительно, если положить , где - произвольная функция, то

,

т.е. - также отвечает заданному значению напряженности . Из (3.5) следует

= = .

Сделаем замену или 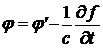. Тогда получим

.

Таким образом, преобразования

(3.6)

не изменяют заданных напряженностей электромагнитного поля, и .

Такие преобразования называют калибровочными или градиентными преобразованиями. Различные способы выбора потенциалов электромагнитного поля, не изменяющие и , называют калибровками потенциалов. Свойство неизменности (инвариантности) и при различных калибровках называют калибровочной (градиентной) инвариантностью.

Калибровочная инвариантность электромагнитного поля позволяет придать уравнениям для потенциалов наиболее простой вид.

Рассмотрим систему уравнений (I) из (3.1). Из первого уравнения системы следует

= = =

= = = .

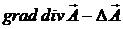После несложных преобразований получим

. (3.7)

Из второго уравнения системы (I) получим еще одно уравнение для потенциалов:

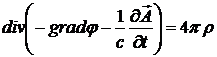
или

. (3.8)

С помощью калибровочных преобразований можно упростить уравнения для потенциалов (3.7) и (3.8). Положим

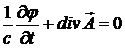. (3.9)

Выражение (3.9) называют условием Лоренца, а соответствующую калибровку потенциалов - калибровкой Лоренца. Покажем, что действительно существует такая калибровка, при которой выполняется условие (3.9).

При произвольном выборе и имеем

.

Произведем калибровочное преобразование

Получим

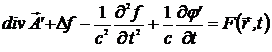. (3.10)

Если подчиняется уравнению Даламбера

,

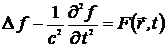то выполняется условие Лоренца

.

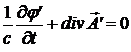В случае калибровки Лоренца из (3.7) и(3.8) следует

(3.11)

Эти уравнения эквивалентны исходной системе уравнений Максвелла.

Введем оператор Даламбера

.

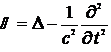Тогда уравнения для потенциалов примут следующий вид:

, . (3.12)

Наряду с лоренцевской калибровкой используется калибровка Кулона, для которой выполняется условие . Уравнения для потенциалов в кулоновской калибровке:

, . (3.13)

Название калибровки «кулоновской» связано с последним уравнением (3.13), так как в случае электростатики из этого уравнения находится потенциал электростатического (кулоновского) поля.

4. Стационарные поля в вакууме. Уравнения для потенциалов статических полей. Общее решение Пуассона.

Простейшая задача теории электромагнитного поля – стационарная задача, т.е. такая задача в которой все величины, входящие в уравнения Максвелла, не зависят от времени. Это означает, что .

Система уравнений Максвелла распадается на две несвязанные подсистемы – электрическую и магнитную

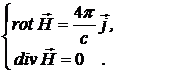(I) (II) (4.1)

· Электростатика.

Рассмотрим случай, когда заряды неподвижны. Тогда 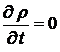и .

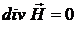Из системы (II) следует, что и . Следовательно, имеет место тривиальное решение .

Из первого уравнения системы (I) имеем для напряженности электростатического поля и . Окончательно получим для скалярного потенциала уравнение Пуассона:

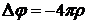, (4.2)

которое является основным уравнением электростатики.

Рассмотрим точечный заряд . Симметрия задачи сферическая и поэтому решение уравнения (4.2) также обладает сферической симметрией, т.е. . Тогда

, (4.3)

Окружим заряд сферой радиуса с центром в точке нахождения заряда . Вычислим интеграл

= = .

Окончательно получим:

. (4.4)

Решение уравнения (4.4)

. (4.5)

При положим . Потенциал поля точечного заряда :

, (4.6)

а напряженность поля

. (4.7)

Работа сил электростатического поля по перемещению единичного заряда из точки в точку

Не нашли, что искали? Воспользуйтесь поиском: