Порождающая и проверочная матрицы циклического кода

Пример 2.1 Четыре строки порождающей матрицы для циклического кода (7,4) с порождающим полиномом 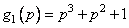можно получить из полиномов

Легко видеть, что порождающая матрица равна

. (2.1)

Аналогично, порождающая матрица для циклического кода (7,4), образуемая порождающим полиномом 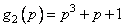, равна

. (2.2)

Проверочные матрицы, соответствующие и , можно сконструировать аналогичным образом, используя соответствующие обратные полиномы (задача 8.8).

Заметим, что порождающие матрицы, полученные таким конструированием, не имеют систематическую форму. Мы можем сконструировать порождающую матрицу циклического кода в систематической форме от порождающего полинома следующим образом. Для начала заметим, что 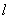-ая строка соответствует полиному формы , где - полином степени, меньшей чем . Эту форму можно получить делением на . Таким образом, имеем

или, что эквивалентно

, (2.3)

где - частное. Но представляет кодовое слово в циклическом коде, поскольку . Следовательно, желательный полином, соответствующий 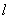-й строке , равен .

Пример 2.2 Для циклического кода (7,4) с порождающим полиномом 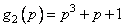, ранее рассмотренного в примере 2.1, имеем

Следовательно, порождающая матрица кода в систематической форме

(2.4)

и соответствующая проверочная матрица

(2.5)

Метод конструирования порождающей матрицы в систематической форме согласно (2.4) также подразумевает, что систематический код можно генерировать непосредственно из порождающего полинома . Предположим, что мы умножим полином сообщения на . Тогда получим

В систематическом коде этот полином представляет первые 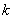бит слова 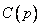. К этому полиному мы должны прибавить полином степени меньшей, чем , представляющей проверочные символы. Теперь, если разделить на , результат равен

или

, (2.6)

где имеет степень меньшую, чем . Ясно, что 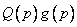- это кодовое слово циклического кода. Следовательно, суммируя (по 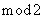) с обеими частями (2.6), мы получаем желаемый систематический код.

Подытоживая, скажем, что систематический код можно генерировать так:

1. Умножаем полином сообщения на ;

2. Делим на , чтобы получить остаток ; и

3. Добавляем к .

Ниже мы продемонстрируем, как эти вычисления можно выполнить, используя сдвиговые регистры с обратной связью.

Поскольку 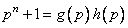или, что эквивалентно, , мы видим, что полиномы и 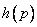ортогональны. Далее, полиномы и также ортогональны для всех и . Однако, векторы, соответствующие полиномам и 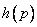, ортогональны только, если порядок следования элементов одного из этих векторов реверсировать. То же утверждение применимо к векторам, соответствующим полиномам и . Действительно, если проверочный полином 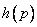используется как порождающий для дуального кода, ансамбль кодовых слов, полученный так, включают в себя те же кодовые слова, которые генерируются обратным полиномом, за исключением того, что кодовые векторы реверсированы. Это подразумевает, что порождающая матрица для дуального кода, полученная от обратного полинома , может быть также получить непосредственно от 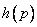. Поскольку проверочная матрица для циклического кода 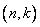является порождающей матрицей для дуального кода, следует, что также можно получить от 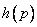. Следующий пример иллюстрируют это соотношение.

Пример 2.3 Дуальный код для циклического кода (7, 4), порождаемого полиномом 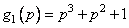- это код (7,3), который порождается обратным полиномом . Однако, мы можем также использовать для получения порождающей матрицы для дуального кода. Матрица, соответствующая полиному равна

Порождающая матрица для дуального кода (7, 3), которая является проверочной матрицей для циклического кода (7, 4), состоит из строк , взятых в инверсном порядке.

Таким образом,

Читатель может убедиться, что .

Заметив, что вектор , состоит из всех семи двоичных вектор-столбцов длины 3, исключая вектор из одних нулей. Но это как раз описание проверочной матрицы для кода Хемминга (7, 4). Следовательно, циклический код (7, 4) эквивалентен коду Хемминга (7, 4), рассмотренному ранее в примерах 1.1 и 1.2.

Не нашли, что искали? Воспользуйтесь поиском: