
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Совершенная дизъюнктивная нормальная форма.
Дизъюнктивной нормальной формой (ДНФ) называется форма представления функции, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждая из которых является простой конъюнкцией аргументов или их инверсий.
Примером ДНФ может служить выражение:

Приведем форму представления функций, не являющейся ДНФ. Например, функция

представлена не в ДНФ, так как последний член не является простой конъюнкцией аргументов.
Также не является ДНФ следующая форма представления функции:
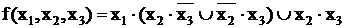 .
.
Если в каждом члене ДНФ представлены все аргументы (или их инверсии) функции, то такая форма носит название совершенной дизъюнктивной нормальной формы (СДНФ). Приведенный выше пример ДНФ не является СДНФ, так как в нем лишь третий член содержит все аргументы функции.
Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида 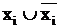 , где xi – отсутствующий в члене аргумент. Так как
, где xi – отсутствующий в члене аргумент. Так как  , такая операция не может изменить значений функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:
, такая операция не может изменить значений функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:

Добавим в члены выражения вида 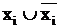 и раскроем скобки:
и раскроем скобки:

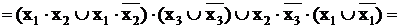
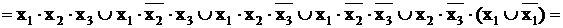
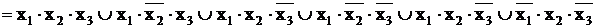
На основании того, что 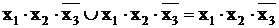 приведем подобные члены и получим:
приведем подобные члены и получим:
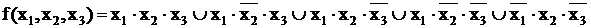
Полученная форма является СДНФ. Дизъюнктивной, как сумма произведений, совершенной, поскольку в каждое произведение входят все переменные и нормальной – в любом произведении каждая переменная встречается лишь однажды. Если исходная функция дана в табличной форме, то СДНФ может быть получена непосредственно.
Если функция задана таблицей истинности, можно сформулировать следующее правило записи её СДНФ: необходимо записать столько членов в виде конъюнкции всех аргументов, сколько единиц содержит функция в таблице. Каждая конъюнкция должна соответствовать определенному набору значений аргументов, обращающему функцию в единицу, и если в этом наборе значение аргумента равно нулю, то в конъюнкцию входит инверсия данного аргумента.
Составим СДНФ для функции, таблица истинности которой представлена таблицей 1.
Таблица 1. Таблица истинности функции f(x1,x2,x3).
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| f |
В представленной таблице функция f(x1,x2,x3) равна «1» во 2, 3, 5, 7-м столбцах наборов значений аргументов. Каждый из этих наборов обращает в единицу соответствующий член составляемого выражения (каждую из конъюнкций в составляемой дизъюнкции), вследствие чего и вся функция оказывается равной единице. Запишем соответствующие наборы аргументов или их инверсий и получим СДНФ функции:
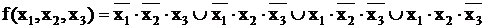
Следует отметить, что любая функция имеет единственную СДНФ.
Не нашли, что искали? Воспользуйтесь поиском: