Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления

Задачи вариационного исчисления – это задачи поиска экстремума функционала или отображения, которое переводит вектор-функции из некоторого подмножества функционального пространства в числа. Таким образом, особенность задач вариационного исчисления состоит в том, что неизвестными являются функции. Множество допустимых решений задачи представляет собой подмножество некоторого функционального пространства. Допустимые решения удовлетворяют общим требованиям для элементов пространства, например, непрерывности, дифференцируемости и т.д., а также ограничениям и связям между неизвестными.

Общая постановка:

J (x (*), u (*)) 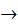inf(sup), (1)

G ₁(t, x (t), x ’(t), u (t)) = 0, G 2 (t, x (t), x ’(t), u (t)) <= 0, (2)

u (t) U (t) R^r, (3)

(t 0, x (t 0), t ₁, x (t ₁)) Г, (4)

охватывает большинство задач оптимального управления и вариационного исчисления [4].

Переменные x = (x ¹,…, xⁿ) называют фазовыми переменными, а u =(u ¹,.., u^r) – управлениями.

Функционал J может быть функционалом одного из следующих трех типов. Интегральный функционал имеет следующую форму:

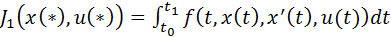, где функция f: R × Rⁿ × Rⁿ × R^r 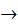R называется интегрантом. Функционалы вида J ₂ (x (*)) = (t ₀, x (t ₀), t ₁, x (t ₁)), где y: R × Rⁿ × R × Rⁿ 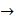R, называются терминальными. Если функционал представим в виде суммы интегрального и терминального функционалов, то он называется функционалом смешанного типа.

Ограничения вида (2), где Gi: R × Rⁿ × Rⁿ × R^r R^ki, i = 1,2, называются функциональными, а ограничения вида (3) – нефункциональными.

Граничные условия задаются выделением в пространстве R × Rⁿ × R × Rⁿ подмножества Г, которому должны принадлежать концы траектории, то есть точка (t ₀, x (t ₀), t ₁, x (t ₁)). Как правило, рассматриваются следующие граничные условия:

– закрепленные, когда значения траектории закреплены на обоих концах отрезка [ t 0, t 1], при этом сам отрезок предполагается фиксированным: x (t 0) = x 0, x (t 1) = x 1;

– свободный правый или левый конец, когда соответствующий конец отрезка [ t 0, t 1] предполагается фиксированным, но на нем нет условия на фазовую траекторию;

– периодические, когда отрезок [ t 0, t 1] фиксирован и фазовая траектория принимает равные значения на концах.

Отрезок [ t 0, t 1] не предполагается закрепленным. Если же он фиксируется, то соответствующую задачу называют задачей с закрепленным временем.

Если функционал (1) является интегральным, то задача (1) – (4) называется задачей Лагранжа; если функционал терминальный, то она называется задачей Майера и, наконец, если функционал смешанный, то соответствующая задача называется задачей Больца.

Все три постановки являются в значительной мере равносильными. Если,например, задан интегральный функционал, то, введя новую координату xn +1 и пополнив систему (2) уравнением x ’ ^{n +1} - f = 0 с граничным условием x^{n +1} (t₀) =, задача о минимизации функционала

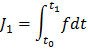
сводится к задаче минимизации терминального функционала J 2 = xⁿ⁺¹(t₁).

Наоборот, если требуется минимизировать терминальный функционал J 2 =y (t 1, x (t 1)) при фиксированных значениях t 0 и x (t 0), то, предполагая, что функция y дифференцируема, положим

откуда получим, что J 2 =y (t 1, x (t 1)) = J 1.

Особенности задач классического вариационного исчисления состоят в следующем. Во-первых, в задачах классического вариационного исчисления все функции, входящие в описание задачи, предполагаются гладкими, по меньшей мере непрерывно дифференцируемыми. С другой стороны, в них отсутствуют нефункциональные ограничения вида (3). В задачах оптимального управления нефункциональные ограничения играют весьма существенную роль. Само по себе множество U (t), задающее ограничение (3), может иметь самую разнообразную природу, например, оно может быть дискретным множеством. Это делает неестественным рассмотрение в задачах оптимального управления гладких и даже непрерывных управлений, а вместе с этим и допущение о гладкости отображений G 1, G 2 в (2) по управлению u. Так что стандартные допущения в задачах вариационного исчисления – непрерывная дифференцируемость по всем переменным, а в задачах оптимального управления – непрерывность по совокупности переменных и гладкость по переменным t и x.

Приведем несколько примеров частных задач, укладывающихся в общую схему.

Простейшей векторной задачей называется задача следующего вида: (5)

В (5) отрезок [ t 0, t 1] предполагается фиксированным, функция L – определенной и непрерывно дифференцируемой в некоторой области пространства R × Rⁿ × Rⁿ; множество G, задающее граничные условия, предполагается произвольным подмножеством пространства Rⁿ × Rⁿ. Если n = 1, то задачу (5) называется простейшей задачей.

Задачей Лагранжа с ограничениями в разрешенной форме и фазовыми ограничениями типа равенств и неравенств называют следующую задачу: 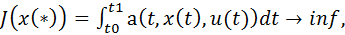(6)

x’ = j (t, x, u), (7)

g 1(t, x (t)) = 0, g 2 (t, x (t)) £ 0, (8)

h 0(t 0, x (t 0)) = 0, h 1(t 1, x (t 1)) = 0, (9)

u U. (10)

Здесь интегральный функционал не зависит от x ’. Ограничения разделены на разрешенные – (7) и фазовые – (8). Граничные условия описываются соотношениями (9). В такой форме можно задать не все встречающиеся в приложениях граничные условия. Например, периодические условия таким путем описать нельзя. Но вместе с тем, соотношения (9) дают возможность выразить достаточно широкий класс граничных условий.

При рассмотрении задачи Лагранжа в рамках классического вариационного исчисления будем предполагать, что отрезок [ t 0, t 1] является фиксированным и ограничение (10) отсутствует.Задача (6) – (10) называется автономной, если во всех входящих в ее определение функциях и отображениях отсутствует явная зависимость от времени.

Линейными задачами оптимального управления будем называть задачи с закрепленным временем следующего вида:

x ’ = A (t) x + B (t) u,

(gi (y), x (t)) <=a i (t), i = 1,…, m,

(h_kj, x (tk)) = b _kj, k = 0,1, j =1,…, sk, u U.

Не нашли, что искали? Воспользуйтесь поиском: