Колебания и волны в одномерной атомной цепочке.

Рассмотрим совокупность ионов массой M, вдоль прямой в точках, отстоящих друг от друга на расстоянии a,так что векторы одномерной решётки Бравэ есть просто R = na, где n – целое число. Пусть u( n a) – отклонение иона в точке na вдоль прямой, отсчитываемое от его равновесного пложения. Оно описывает смещение иона вблизи точки na см. рис.

Для простоты предположим,что взаимодействуют лишь соседние ионы; тогда потенциальная энергия будет иметь вид

. (5.2.1)

После определения силы как производной от потенциальной энергии можем записать уравнения движения в форме Ньютона

. (5.2.2)

Если число ионов в цепочке, конечно, необходимо указать, как описывать ионы на двух её концах. Однако, если число ионов велико и нас не интересуют эффекты, происходящие наконцах цепочки мы можем воспользоваться подходом, который даёт наибольшие математические преимущества. Как и в случае электронного газа, удобнее всего выбрать периодические циклические условия Борна–Кармана. Для линейной цепочки это граничное условие допускает простую формулировку: мы соединяем два противоположных конца цепочки, тем самым, отождествляя ион номер 1, с ионом номер N +1. Таким образом, для решений получаем следующие условия 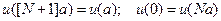. Будем искать решение уравнений Ньютона в виде . Тогда из периодического граничного условия вытекает требование 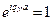, откуда в свою очередь следует, что величина q должна иметь следующий вид

, n – целое число. (5.2.2а)

Заметим, что при изменении q на смещение , не меняется. Следовательно, имеется лишь N значений q, согласующихся с требованиями граничных условий и дающих физически различные решения. Будем считать, что эти значения лежат в интервале от значения до . Так в одномерном случае выглядит требование, чтобы вектор q лежал в первой зоне Бриллюэна. После подстановки предлагаемого решения в уравнение Ньютона получим

(5.2.3)

Решение этого уравнения существует, если , где

. (5.2.4)

Решения, описывающие реальные смещения частиц, даются действительной или мнимой частью

или .(5.2.5)

Поскольку – чётная функция q, достаточно взять лишь положительный корень в (5.2.4): решения (5.2.5), определяемые значенмями q и , совпадают с решениями, определяемые значениями – q и 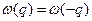. Таким образом, мы имеем N различных значений q, каждое со своей частотой 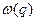; следовательно, формулы (5.2.5) дают 2 N независимых решений. Произвольное движение цепочки задаётся указанием N начальных положений и N начальных скоростей ионов. Поскольку начальным условиям всегда можно удовлетворить, выбрав подходящую комбинацию из 2 N независимых решений, мы нашли полное решение задачи.

Решения (5.2.5) описывают волны, распространяющиеся вдоль цепочки с фазовой скоростью 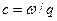и групповой скоростью . Волны u(qa,t) называются нормальными колебаниями, а частоты модами нормальных колебаний. Частота как функция волнового вектора q изображена на рис. Такую кривую называют дисперсионной. Когда значение q мало по сравнению со значением (т.е. когда длина волны велика по сравнению с расстоянием между частицами), частота линейно зависит от q

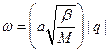. (5.2.6)

Такое поведение волн, как известно, присуще и световым и звуковым волнам. На рис. прямой линией показана дисперсия звуковых волн. Если частота линейно зависит от q, то групповая скорость совпадает сфазовой и обе они не зависят от частоты. Однако, в дискретных средах, характерная особенность волн проявляется в том, что линейный закон дисперсии перестаёт соблюдаться при длинах волн, сравнимых с расстоянием между частицами. В этом случае отстаёт от фазовой скорости с ростом q и в действительности в точках дисперсионная кривая становится горизонтальной, т.е. групповая скорость спадает до нуля.

Не нашли, что искали? Воспользуйтесь поиском: