
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Краткие теоретические сведения. В различных практических задачах часто возникает необходимость обобщить полученную в процессе исследования информацию с целью построения аналитических
В различных практических задачах часто возникает необходимость обобщить полученную в процессе исследования информацию с целью построения аналитических зависимостей, пригодных для использования в имитационных и прогнозных моделях, в выявлении закономерностей. Все процессы и явления, в той или иной степени взаимосвязаны друг с другом. С помощью статистических методов можно установить зависимость и дать ей количественную характеристику. Простейшей формой связи является линейная зависимость. Далее будем рассматривать взаимосвязь двух признаков Х и Y.
На практике для самых разнообразных явлений массового характера имеет место стохастическая зависимость, т.е. признаки Х и Y связаны между собой, но эта взаимосвязь между переменными не однозначна, а подвержена случайным изменениям, т.е. при определенном значении признака Х признак Y принимает заранее не предсказуемое значение. Это объясняется тем, что кроме признака Х на изменчивость Y влияет много других, не учтенных связей.
Стохастическую зависимость можно изучать методами корреляционного и регрессионного анализа. Корреляционная связь определяет наличие и форму связи, тесноту этой связи, устанавливает и анализирует зависимость между значениями одной переменной и соответствующими ей среднегрупповыми значениями другой. Для выяснения вида зависимости между х и  используют графическое изображение выборки, а именно: диаграмму рассеяния или корреляционное поле. Диаграммой рассеяния называется совокупность п точек плоскости с координатами (х 1, у 1), (х 2, у 2), …, (хn, уn), где х 1, х 2, …, хп - значения признака Х, а у 1, у 2, …, уп - соответствующие значения признака Y. Построив диаграмму рассеяния, визуально определяют наличие и направление связи, величину разброса значений. Так же можно сделать предположение о виде корреляционной зависимости: линейной, квадратичной и др. Рисунок 6.1а иллюстрирует наличие тесной, положительно ориентированной линейной связи. На рисунке 6.1б показан случай, когда связь менее тесная и отрицательно ориентирована, и на рисунке 6.1в представлена диаграмма нелинейной связи между величинами Х и Y.
используют графическое изображение выборки, а именно: диаграмму рассеяния или корреляционное поле. Диаграммой рассеяния называется совокупность п точек плоскости с координатами (х 1, у 1), (х 2, у 2), …, (хn, уn), где х 1, х 2, …, хп - значения признака Х, а у 1, у 2, …, уп - соответствующие значения признака Y. Построив диаграмму рассеяния, визуально определяют наличие и направление связи, величину разброса значений. Так же можно сделать предположение о виде корреляционной зависимости: линейной, квадратичной и др. Рисунок 6.1а иллюстрирует наличие тесной, положительно ориентированной линейной связи. На рисунке 6.1б показан случай, когда связь менее тесная и отрицательно ориентирована, и на рисунке 6.1в представлена диаграмма нелинейной связи между величинами Х и Y.
Рисунок 6.1а Рисунок 6.1б Рисунок 6.1в
Замечание. При построении диаграммы масштаб на осях координат следует выбирать так, чтобы размахи варьирования обоих переменных:  и
и  были приблизительно равными.
были приблизительно равными.
Если точки диаграммы рассеяния сосредоточены возле некоторой прямой, т.е. можно предположить, что корреляционная связь между признаками Х и Y является линейной (рис.6.1а, б), то эту зависимость можно характеризовать функцией регрессии  по
по  вида:
вида:
 , (6.1)
, (6.1)
где 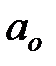 и
и  - неизвестные коэффициенты такой зависимости.
- неизвестные коэффициенты такой зависимости.
Определение числовой оценки тесноты линейной корреляционной связи между признаками Х и Y осуществляется при помощи так называемого выборочного коэффициента корреляции 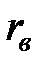 .
.
Вначале исследуется каждый признак Х и Y в отдельности, а именно, находят соответствующие признакам Х и Y средние выборочные  и
и  и выборочные стандартные отклонения
и выборочные стандартные отклонения  и
и  по формулам, которые выписаны в теме 5.
по формулам, которые выписаны в теме 5.
Если число выборочных данных невелико и частоты  , то формула (5.1) для вычисления
, то формула (5.1) для вычисления  может быть записана в виде:
может быть записана в виде:
 , (6.1)
, (6.1)
соответственно для вычисления  эта формула примет вид:
эта формула примет вид:
 . (6.2)
. (6.2)
Для вычисления выборочных стандандартных отклонений, используя формулы (5.9) и (5.6) и, учитывая, что  , получим:
, получим:
 , (6.3)
, (6.3)
 . (6.4)
. (6.4)
Следующий этап статистического исследования - это установление зависимости между Х и Y.
В общей постановке эта задача неразрешима, т.к. одному значению признака Х может соответствовать целый спектр значений признака Y. Поэтому поставим более узкую задачу. Определим корреляционную зависимость между признаками Х и Y, при которой происходит изменение среднего значения одного из признаков при изменении значений другого признака.
Пусть  - среднее значение признака Y, когда признак Х принимает значение, равное х. Для нахождения линейной корреляционной зависимости между признаками Х и Y вначале определяют уровень (тесноту) этой зависимости, т.е. вычисляют выборочный коэффициент корреляции
- среднее значение признака Y, когда признак Х принимает значение, равное х. Для нахождения линейной корреляционной зависимости между признаками Х и Y вначале определяют уровень (тесноту) этой зависимости, т.е. вычисляют выборочный коэффициент корреляции 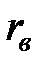 по формуле:
по формуле:
 , (6.5)
, (6.5)
где  - среднее значение произведений соответствующих выборочных значений признаков Х и Y, т.е. при
- среднее значение произведений соответствующих выборочных значений признаков Х и Y, т.е. при  имеем
имеем  , а произведение
, а произведение  - есть произведение средних значений. Итак, формула (6.5) при
- есть произведение средних значений. Итак, формула (6.5) при  примет вид:
примет вид:

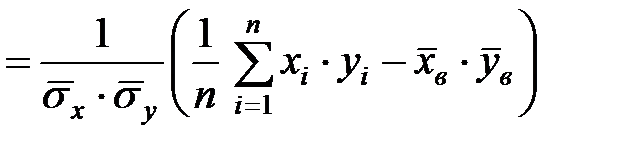 . (6.6)
. (6.6)
Выборочный коэффициент корреляции является величиной безразмерной и его значение находится в пределах от -1 до +1, т.е.
 .
.
Выборочный коэффициент корреляции характеризует линейную связь между признаками Х и Y:
Если  близок к 1, то эта связь тесная.
близок к 1, то эта связь тесная.
Если  близок к 0, то эта связь слабая.
близок к 0, то эта связь слабая.
Если  >0, то говорят, что связь между признаками Х и Y положительно ориентирована, т.е.
>0, то говорят, что связь между признаками Х и Y положительно ориентирована, т.е.  , в основном, возрастает при возрастании х (рис. 6.1а).
, в основном, возрастает при возрастании х (рис. 6.1а).
Если  < 0, то говорят, что связь между признаками Х и Y отрицательно ориентирована, т.е.
< 0, то говорят, что связь между признаками Х и Y отрицательно ориентирована, т.е.  , в основном, убывает при возрастании х (рис. 6.1б).
, в основном, убывает при возрастании х (рис. 6.1б).
Пусть корреляционная зависимость между признаками Х и Y является линейной, тогда уравнение регрессии  , можно записать в виде:
, можно записать в виде:
 (6.7)
(6.7)
Выборочное уравнение линейной регрессии используется при статистических исследованиях для вычисления предполагаемых средних значений одного из признаков, когда известно значение другого.
Вопросы для самоконтроля
1. Дайте определение поля корреляции и опишите методы его построения.
2. Что определяет корреляционная зависимость?
3. Что характеризует выборочный коэффициент корреляции?
4. Опишите алгоритм определения выборочного коэффициента линейной корреляции.
5. Когда имеет смысл строить уравнение линейной регрессии?
6. Как произвести расчет коэффициентов линейного уравнения регрессии с использованием коэффициента корреляции?
Пример 6.1 При изучении химического состава плодов черники было обследовано десять образцов ягод и получены следующие данные о содержании сухих веществ Х (%) и органических кислот Y (%) в исследуемых образцах:
| Сухое вещество Х (%) | 14,5 | 14,8 | 14,0 | 15,1 | 15,3 | 13,5 | 14,9 | 14,8 | 15,0 | 14,3 |
| Органические кислоты Y (%) | 1,2 | 1,22 | 0,95 | 1,34 | 1,42 | 1,1 | 1,22 | 1,3 | 1,23 | 1,1 |
Выполнить следующую статистическую обработку данных:
Выполнить следующую статистическую обработку данных:
1) построить диаграмму рассеяния;
2) полагая, что между признаками  и
и 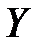 имеет место линейная корреляционная зависимость определить выборочный коэффициент корреляции
имеет место линейная корреляционная зависимость определить выборочный коэффициент корреляции 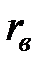 , сделать вывод о направлении и тесноте этой связи;
, сделать вывод о направлении и тесноте этой связи;
3) найти выборочное уравнение линейной регрессии. Используя полученное уравнение, оценить ожидаемое среднее значение признака 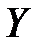 , когда признак
, когда признак  примет значение
примет значение  =14,7 (%);
=14,7 (%);
4) построить линию регрессии на том же рисунке, на котором построена диаграмма рассеяния.
Решение:
1) Построим диаграмму рассеяния (рис.6.1)

Рисунок 6.1
2) По расположению точек на диаграмме, можно говорить о наличии убывающей линейной корреляционной зависимости. Определим выборочный коэффициент корреляции 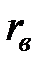 по формуле (6.6). Для этого составим расчетную таблицу и найдем суммы по всем ее столбцам.
по формуле (6.6). Для этого составим расчетную таблицу и найдем суммы по всем ее столбцам.
Вычислим выборочные характеристики для признаков Х и Y:

| 
| 
| 
| 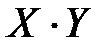
| |
| 14,5 | 1,2 | 210,25 | 1,44 | 17,4 | |
| 14,8 | 1,22 | 219,04 | 1,484 | 18,056 | |
| 0,95 | 0,905 | 13,3 | |||
| 15,1 | 1,34 | 228,01 | 1,7956 | 20,234 | |
| 15,3 | 1,42 | 234,09 | 2,0164 | 21,726 | |
| 13,5 | 1,1 | 182,25 | 1,21 | 14,85 | |
| 14,9 | 1,22 | 222,01 | 1,4884 | 18,178 | |
| 14,8 | 1,3 | 219,04 | 1,69 | 19,24 | |
| 1,23 | 1,5129 | 18,45 | |||
| 14,3 | 1,1 | 204,49 | 1,21 | 15,73 | |

| 146,2 | 12,08 | 2140,18 | 14,7542 | 177,164 |
Используя полученные результаты, вычислим выборочные средние и выборочные стандартные отклонения признаков X и Y:
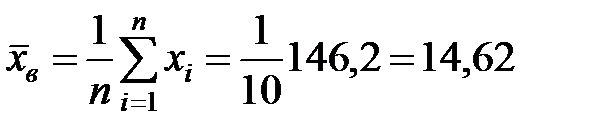 ;
;
 ;
; 
=  ;
; 
 .
.
Вычислим выборочный коэффициент корреляции по формуле (6.6):  =
=
 .
.
Выборочный коэффициент корреляции положителен и близок к 1. Следовательно, между признаками  и
и 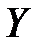 имеет место тесная положительно ориентированная линейная корреляционная зависимость.
имеет место тесная положительно ориентированная линейная корреляционная зависимость.
3) Найдем выборочное уравнение линейной регрессии, используя формулу (6.7).

 .
.
Итак, уравнение линейной регрессии имеет вид:
 .
.
3) Используя полученное уравнение, оценим ожидаемое среднее значение признака 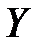 , когда признак
, когда признак  примет значение, равное 14,7 (%), т.е. подставим в полученное уравнение регрессии
примет значение, равное 14,7 (%), т.е. подставим в полученное уравнение регрессии  . Получим
. Получим  .
.
Следовательно, ожидаемое среднее значение процентного содержания органических кислот в плодах черники, когда содержание сухих веществ равно 14,7%, близко к 1,22%.
4)Построим прямую линию регрессии на рисунке 6.1. Для этого определим координаты двух любых точек этой прямой:
Найдем координаты двух точек этой прямой:
при  , т.е.
, т.е.  ;
;
при  , т.е.
, т.е.  .
.
Не нашли, что искали? Воспользуйтесь поиском: