Уравнение Христиановича-Желтова-Геертсма-деКлерка

В первой модели гидроразрыва пласта, разработанной Христиановичем и Желтовым [Khristianovich and Zheltov, 1955], рассматривалась трещина одной и той же ширины на любой вертикальной координате в пределах фиксированной высоты 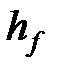. В основе лежала физическая гипотеза, что поверхности трещины свободно скользят по кровле и подошве пласта. В результате получается трещина прямоугольного сечения. Ширина трещины рассматривается как функция координаты x. Она определяется из допущения о плоской деформации, теперь приложенной в (каждой) горизонтальной плоскости. Модель Кристиановича и Желтова содержала еще одно интересное допущение: существование несмоченной зоны возле вершины трещины. Геертсма и деКлерк [Geertsma and deKlerk, 1969] приняли основные допущения Кристиановича и Желтова и свели эту модель к явной формуле для ширины. Уравнение ширины KGD следующее:

(4-20)

В этом случае коэффициент формы, выражающий связь средней ширины с шириной у скважины, не имеет вертикальной составляющей. Затем, из-за эллиптической горизонтальной формы, мы получаем

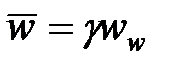, где 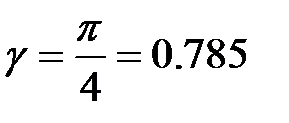(4-21)

Расширение модели KGD, разработанное Данеши [Daneshy, 1978], рассматривает непостоянное распределение давлений по длине трещины, причем неньютоновские свойства жидкости разрыва могут изменяться с временем и температурой. Численные расчеты дают удельную утечку, увеличение ширины и скорость потока в точках по длине трещины в течение периода удлинения трещины.

Для коротких трещин, где 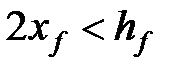, более приемлемо допущение о плоской деформации в горизонтальной плоскости (геометрия KGD), а для — бóльший физический смысл имеет допущение о плоской деформации в вертикальной плоскости (геометрия PKN). Интересно, что для особого случая, когда общая длина и высота трещины эквивалентны, эти два уравнения дают в основном одинаковую среднюю ширину и, следовательно, объем трещины.

Уравнение ширины для радиальной геометрии (трещина в форме пятака)

Эта ситуация соответствует горизонтальным трещинам из вертикальных скважин, вертикальным трещинам, отходящим от горизонтальных скважин, или гидроразрыву относительно мощных однородных пластов из ограниченных перфорированных интервалов во всех случаях. В то время как расчеты ширины трещины чувствительны к тому, как жидкость входит в трещину (истинно точечный источник приводит к бесконечному давлению), можно постулировать разумную модель по аналогии, в результате которой мы имеем ту же среднюю ширину, что и для уравнения Перкинса-Керна, когда .

Этот результат следующий:

(4-22)

Реальная значимость простых моделей, представленных в этом разделе, состоит в более углубленном взгляде на задачу — они помогают нам рассмотреть влияние исходных данных на развитие трещины. Еще лучше разобраться в этом может помочь сравнение геометрии трещин и поведения эффективного давления для этих моделей. В таблице 4-4 непосредственно сопоставлены основные модели трещины (для случая нулевой утечки).

Особого внимания заслуживает последняя строка таблицы 4-4. Для случая нулевой утечки: по модели Перкинса-Керна эффективное давление увеличивается во времени, но для двух других моделей — уменьшается во времени. Это хорошо известный результат, который поднимает несколько вопросов. Например, при массивном гидроразрыве в некоторых случаях эффективное давление чаще всего растет во времени, так что эффективные давления, полученные из модели Геертсма-деКлерка и радиальной модели, имеют ограниченное практическое значение. Более удивительное (и не столь широко известное) наблюдение заключается в том, что эффективные давления, получаемые по модели Геертсма-деКлерка и по радиальной модели, не зависят от темпа нагнетания. Из постулатов модели KGD (и в радиальной тоже) вытекает, что когда размеры трещины становятся очень большими, требуются очень малые эффективные давления для поддержания определенной ширины. Хотя это является следствием теории линейной упругости и того способа, как применено допущение о плоской деформации, в целом это приводит к абсурдным результатам. Можно с уверенностью сказать, что модель PKN лучше описывает физику процесса гидроразрыва, чем две другие модели.

Хотя за последние полвека было выполнено множество исследований, в любой предлагаемой модели всегда должны быть некоторым образом «замешаны» одни и те же ингредиенты: материальный баланс, связывающий темп нагнетания и объем трещины; линейная упругость, связывающая ширину трещины и ее линейные размеры; а также механика флюидов, связывающая ширину и падение давления вдоль трещины. Кроме того, может присутствовать или не присутствовать явно выраженный критерий распространения трещины.

ТАБЛИЦА 4-4. Решения для основных моделей трещины при нулевой утечке
Модель	Модель Перкинса и Керна	Модель Геертсма и деКлерка	Радиальная модель
Линейные размеры трещины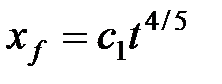

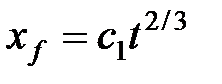
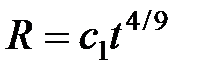
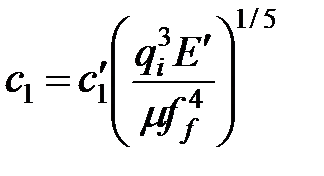
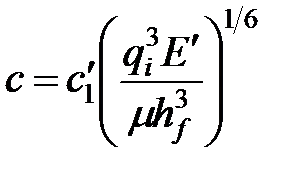
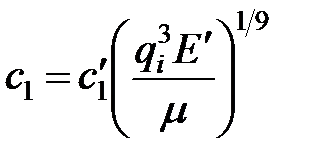
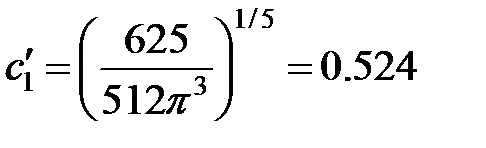
ТАБЛИЦА 4-4. (продолжение) Решения для основных моделей трещины при нулевой утечке
Модель	Модель Перкинса и Керна	Модель Геертсма и деКлерка	Радиальная модель
Ширина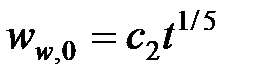
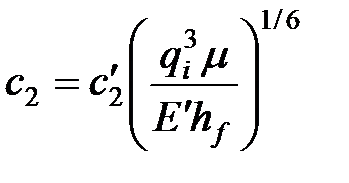
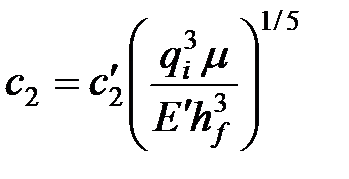
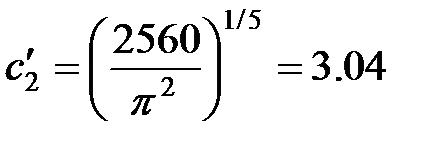
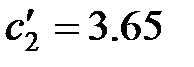
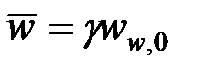
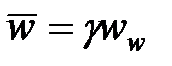
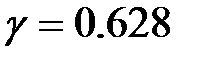
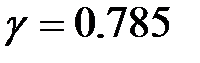
Эффективное давление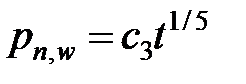

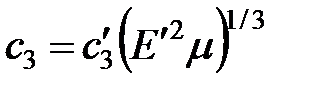
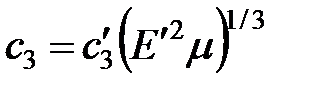
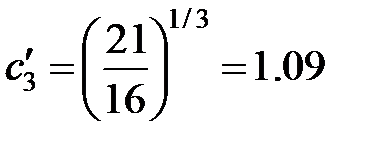
Не нашли, что искали? Воспользуйтесь поиском: