Примеры решения задач 7 страница

На заряженную частицу q в магнитном поле действует – сила Лоренца. Эта сила сообщает заряженной частице центростремительное (нормальное) ускорение a_n.

По второму закону Ньютона

,

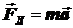где m – масса заряженной частицы,

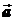‑ ускорение заряженной частицы.

Запишем для заряженной частицы второй закон Ньютона в проекции на ось z:

F_Лz = ma_z,

где

.

Здесь R – радиус окружности.

Так как , то

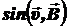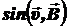F_Л = quB = quB sin a = quB sin 60⁰ = quB, или F_Л = quB = quB sin a = qu_zB.

(u_z = u sin a.)

F_Лz = qu_zB = quB.

Значит,

,

откуда

.

Так как магнитная индукция и напряжённость магнитного поля связаны соотношением

,

а, следовательно,

,

где m₀ = 4p×10^-7 Гн/м – магнитная постоянная;

m ‑ магнитная проницаемость среды (в вакууме m = 1),

то

.

Значит, радиус витка спирали

.

По условию данной задачи заряженной частицей является электрон:

q = e.

Следовательно,

.

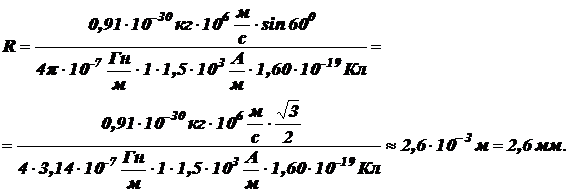
Шаг спирали найдём на основании следующего равенства:

h = T,

где T – период ‑ время, в течение которого заряженная частица продвинется по горизонтальному направлению на один шаг спирали h;

u_y = u cos a.

Итак, с одной стороны, T ‑ время, в течение которого заряженная частица продвинется по горизонтальному направлению на один шаг спирали h. С другой стороны, T равно времени, в течение которого заряженная частица пройдёт со скоростью расстояние, равное длине окружности

l = 2pR,

т.е.

,

или с учётом того, что u_z = u sin a,

.

Следовательно,

.

Так как , то

.

По условию данной задачи заряженной частицей является электрон:

q = e.

Значит,

.

Ответ: 1) ;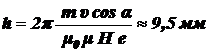

2) .

31. Частица, несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией B = 0,05 Тл. Определить момент импульса L, которым обладает частица, при движении в магнитном поле, если траектория её представляет окружность радиусом R =0,2 мм.

поля) называются линии, проведённые в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля. Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не возвращаясь вторично в любую точку поверхности. Последний случай осуществляется, например, в магнитном поле, создаваемом системой из кругового тока и бесконечного прямолинейного проводника с током, проходящего через центр кругового витка с током, перпендикулярно к его плоскости.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.

Движение заряженной частицы по окружности эквивалентно круговому току. Магнитным моментом контура с током I называется векторная величина , равная

,

где ‑ единичный вектор нормали к элементу dS поверхности S, натянутой на контур с током (ограниченной этим контуром).

Векторы и направлены так, чтобы из их концов ток в контуре был виден идущим против часовой стрелки (рис. 1).

Рис. 1

В случае плоского контура (а по условию данной задачи траектория частицы представляет окружность; окружность находится в плоскости; контур можно представить плоским) поверхность S тоже плоская и все нормали имеют одинаковое направление, поэтому

, p_m = IS.

Значит, подставляя в уравнение выражение для тока

,

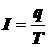где q – заряд частицы,

T – период обращения частицы по орбите,

получим

.

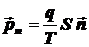Так как заряженная частица движется по круговой орбите (окружности) радиусом R, то S – площадь, ограниченная окружностью, описываемой заряженной частицей, ‑ равна

S = pR².

Длина окружности

l = 2pR,

а

uT = l,

где u ‑ скорость заряженной частицы, движущейся в магнитном поле.

Следовательно,

2pR = uT,

откуда

.

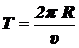Значит,

.

На заряженную частицу в магнитном поле действует – сила Лоренца.

По второму закону Ньютона

,

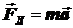где m – масса заряженной частицы,

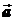‑ ускорение заряженной частицы.

Влетев в однородное магнитное поле, заряженная частица начинает двигаться по круговой орбите, поскольку её скорость перпендикулярна силе Лоренца. Движение частицы по круговой орбите можно представить как движение по окружности со скоростью 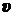под действием силы Лоренца в плоскости, перпендикулярной индукции поля (рис. 2).

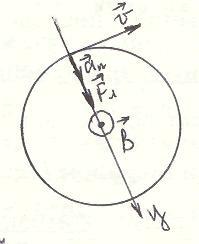
Рис. 2

Запишем для заряженной частицы второй закон Ньютона в проекции на ось y:

F_{Л y} = ma_y,

где

.

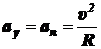Здесь R – радиус окружности.

Так как 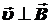, то

F_Л = quB 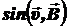= quB sin 90⁰ = quB.

F_{Л y} = quB.

Значит,

,

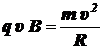откуда

.

Следовательно, магнитный момент эквивалентного кругового тока

.

По условию данной задачи частица несёт один элементарный заряд, а так как элементарный заряд e» 1,60×10^-19 Кл (электрический заряд любой системы тел состоит из целого числа элементарных зарядов, приближённо равных 1,60×10^-19 Кл; наименьшей по массе устойчивой частицей, имеющей отрицательный элементарный заряд, является электрон), то

q = e» 1,60×10^-19 Кл

(см. условие задачи).

Таким образом, магнитный момент эквивалентного кругового тока или орбитальный (поскольку электрон движется по орбите (по окружности)) магнитный момент электрона

.

Моментом импульса (моментом количества движения) материальной точки относительно неподвижной точки O (полюса) называется вектор , равный векторному произведению радиус-вектора , проведённого из полюса O в место нахождения материальной точки, на вектор 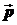её импульса:

,

где m – масса материальной точки,

‑ скорость материальной точки.

Электрон, движущийся по орбите (по окружности), имеет орбитальный момент импульса , который противоположен по направлению вектору орбитального магнитного момента электрона (рис. 3) и связан с ним соотношением

.

Рис. 3

Коэффициент пропорциональности g называется гиромагнитным отношением орбитальных моментов и равен

,

где m – масса электрона.

Следовательно, орбитальный момент импульса

.

Таким образом, момент импульса

.

.

Ответ: .

Не нашли, что искали? Воспользуйтесь поиском: