Методические указания к решению типовых задач. Задача №2.1. Нить в форме полуокружности заряжена равномерно с линейной плотностью t

Задача №2.1. Нить в форме полуокружности заряжена равномерно с линейной плотностью t. С помощью принципа суперпозиции найдите значение напряженности и потенциала в центре соответствующей окружности.

Указания по решению. Рассмотрим элемент нити dl, несущий заряд dq = t×dl. К нему применимы формулы, определяющие поле точечного заряда, т.е.

и .

Т.к. каждый элемент в силу симметрии формы нити имеет симметричный участок (рис. 6), вектор напряженности поля которого симметричен вектору относительно указанной на рисунке оси симметрии, то суммарная напряженность поля будет направлена по оси симметрии и равна сумме проекций векторов на эту ось (проекции на перпендикулярное к этой оси направление взаимно компенсируются).

В соответствии с формулами (2.7) получим значение потенциала поля нити:

.

,

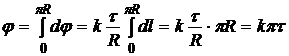тогда

.

Полученные значения относятся лишь к одному частному случаю (к единственной точке – центру), а потому связь (2.2) на этом примере проследить нельзя.

Задача №2.2. Тонкое плоское кольцо радиуса R и толщиной h равномерно заряжено с поверхностной плотностью зарядов s. Найдите с помощью принципа суперпозиции напряженность и потенциал поля в точке, находящейся на перпендикулярной к плоскости кольца оси (проходящей через его центр) на расстоянии х от плоскости кольца. Принять h << R.

Указания по решению. Проведем расчет прямым путем (от потенциала к напряженности) и обратным (от напряженности к потенциалу).

Прямой путь.

Рассмотрим элемент кольца, несущий заряд

и создающий поле с потенциалом

.

Т.к. в качестве элемента взят элемент длины dl, то интегрирование производим по длине кольца (2p R):

.

Полученное выражение для потенциала одинаково верно для любой точки на оси х (рис. 7). Поэтому возможно применение формулы (2.2) для нахождения проекции вектора напряженности на эту ось:

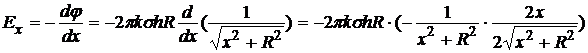Þ

.

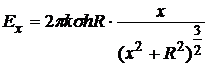Учитывая симметрию, отметим, что сумма перпендикулярных оси х составляющих вектора напряженности поля равна нулю, тогда величина напряженности в любой точке на оси х равна

.

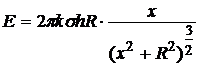Обратный путь.

При суммировании полей элементов кольца перпендикулярные оси х составляющие векторов напряженностей элементарных полей будут компенсировать друг друга в силу симметрии. Поэтому для нахождения напряженности суммарного поля достаточно сложить значения dE_x:

.

Интегрируем по длине кольца:

.

Последнее выражение сравните с полученным ранее.

Для нахождения потенциала воспользуемся соотношением

,

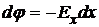тогда

В случае получим:

Сравнение с ранее полученной формулой убеждает в правильности проделанных расчетов.

Отметим, что полный заряд на кольце равен

,

тогда формула для потенциала принимает простой вид

.

Учитывая, что расстояние от заряда кольца до выбранной точки есть

,

получаем формулу по виду в точности совпадающую с формулой потенциала точечного заряда. Аналогичный вывод имеет место и для напряженности.

В заключение отметим, что интегрировать скалярную величину (потенциал) всегда проще, чем векторную (напряженность), а потому прямой путь предпочтительнее.

Указания по решению. По данным задачи, прежде всего, определим поверхностную плотность заряда, учитывая равномерность его распределения по площади круга:

.

В качестве элементарного заряда выберем заряд на тонком кольце (см. рис. 8) радиуса r (r £ R):

dq = s ×2p r × dr.

Прямой путь.

Из предыдущей задачи известно, что потенциал поля элементарного кольца в данной точке равен

Þ

.

Здесь в качестве нулевой точки также взята бесконечно удаленная точка. Действительно: .

Далее используя связь напряженности с потенциалом находим напряженность поля заряженного круга:

.

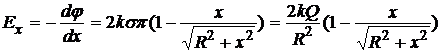Обратный путь. При нахождении напряженности поля с учетом принципа суперпозиции требуется вычислять величину векторной суммы. Для каждого элемента, т.е. тонкого кольца, по результатам предыдущей задачи имеем, что напряженность его поля направлена по оси. Поэтому при сложении одинаково направленных векторов величина суммы будет равна сумме величин напряженностей слагаемых полей:

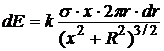Þ

Подставив сюда выражение для плотности заряда, получим то же выражение, что и ранее. Теперь остается определить потенциал:

Полагая , получим

Последняя формула также подтверждает полученный ранее результат.

Задача №2.4. Бесконечная тонкая нить равномерно заряжена с линейной плотностью t. Найдите напряженность и потенциал на расстоянии х от нити.

Указания по решению. Рассмотрим элемент длины dl, несущий заряд

dq = t × dl.

Проекция вектора напряженности поля этого заряда в заданной точке

.

Интегрируем по переменной l:

.

Теперь можно вычислить разность потенциалов между двумя точками х и х ₀ рассматриваемого поля:

.

рис. 9

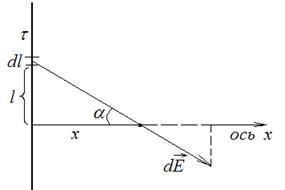Из полученного выражения для потенциала видно, что выбирать в качестве нулевой точки х ₀=¥ нецелесообразно, т.к. в этом случае . Поэтому нулевая точка в этом случае должна быть выбрана на конечном расстоянии от источников поля (выбирается «на свое усмотрение»).

По этой же причине прямой путь для нахождения характеристик поля сопряжен с определенными неудобствами. Т.е. в данном примере обратный путь дает результат более простым способом. На следующем занятии будет изучен еще один метод вычисления значения напряженности поля, наиболее удобный для случая бесконечных размеров заряженных тел как источников поля.

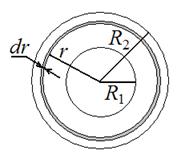Задача №2.5. Определите потенциал j поля в центре кольца с внешним радиусом R ₂=40 см и внутренним R ₁=20 см, если на нем равномерно распределен заряд q =0,6 мкКл.

Указания по решению. По данным задачи, прежде всего, определим поверхностную плотность заряда, учитывая равномерность его распределения по площади кольца:

рис. 10

.

В качестве элементарного заряда выберем заряд на тонком кольце (рис. 10) радиуса r (R ₁ £ r £ R ₂) и толщиной dr:

dq = s ×2p r × dr.

Известно, что потенциал поля элементарного кольца в центре находится по формуле, аналогичной формуле потенциала точечного заряда:

Þ в соответствии с принципом суперпозиции полей в среде с e =1 имеем:

.

Подставляя выражение для поверхностной плотности заряда, окончательно получим выражение для искомой величины:

.

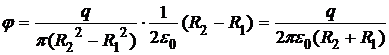Вычислим:

1,8×10⁴ (В).

Здесь в качестве нулевой точки взята бесконечно удаленная точка.

Задача №2.6. Определите линейную плотность бесконечной равномерно заряженной нити, если работа сил поля по перемещению заряда q =1 нКл с расстояния r ₁=5 см до r ₂=14 см в направлении, перпендикулярном нити, равна 65 мкДж.

Указания по решению. Работа потенциальных сил равна убыли потенциальной энергии перемещаемого заряда в этом поле, т.е.

.

Потенциальная энергия взаимодействия заряда с полем выражается через потенциал поля и величину этого заряда:

.

Получаем выражение для работы сил электростатического поля по перемещению заряда q:

.

Изменение потенциала вдоль направления, перпендикулярного нити, выразим как

.

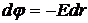Из приложения (3) возьмем формулу напряженности поля бесконечной равномерно заряженной нити:

.

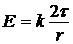Получаем:

.

Искомая работа равна интегралу

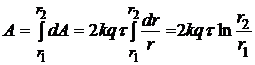Þ

.

Вычисления проведите самостоятельно.

⇐ Предыдущая12345678910Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: