
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Элементы математической теории векторного поля
Говорят, что в некоторой области пространства задано векторное поле, если для любой точки этого пространства задан некоторый вектор, например,  .
.
Пример. Если имеется поток текущей жидкости, то можно рассмотреть в любой точке этого потока вектор скорости  частицы жидкости, находящейся в этой точке.
частицы жидкости, находящейся в этой точке.
|
 1. Определим понятие «вектор элемента площади».
1. Определим понятие «вектор элемента площади».
Пусть дана поверхность S. Рассмотрим малый элемент поверхности с площадью dS (рис. 43). Выберем одну из двух нормалей к элементу в качестве положительной и введем единичный вектор этой нормали  (
( =1). Образуем вектор
=1). Образуем вектор  , модуль которого равен площади элемента и который направлен вдоль положительной нормали к нему. Такой вектор называется вектором элемента площади.
, модуль которого равен площади элемента и который направлен вдоль положительной нормали к нему. Такой вектор называется вектором элемента площади.
2. Определим понятие «поток векторного поля». Здесь возможны 3 случая в зависимости от вида поверхности.
|
 Рассмотрим поле вектора
Рассмотрим поле вектора  , заданного как функция координат точки. В этом поле рассмотрим элемент поверхности, характеризуемый вектором
, заданного как функция координат точки. В этом поле рассмотрим элемент поверхности, характеризуемый вектором  . В силу малости элемента поверхности поле в его пределах представлено вектором
. В силу малости элемента поверхности поле в его пределах представлено вектором  (рис. 44). Образуем скалярное произведение
(рис. 44). Образуем скалярное произведение  ,где ап – нормальная (перпендикулярная) составляющая вектора
,где ап – нормальная (перпендикулярная) составляющая вектора  .
.
Величина  показывает, в какой мере элемент поверхности dS пронизывается векторным полем и называется потоком вектора
показывает, в какой мере элемент поверхности dS пронизывается векторным полем и называется потоком вектора  через элемент dS.
через элемент dS.
Если просуммировать (проинтегрировать) такие величины по всей некоторой конечной поверхности S произвольной формы (предварительно разбив ее на малые элементы и проделав для них описанную выше процедуру), то получим величину
 ,
,
называемую потоком поля через заданную конечную поверхность.
Пример. В гидродинамике поток вектора скорости определяет объем жидкости, ежесекундно протекающей через поверхность.
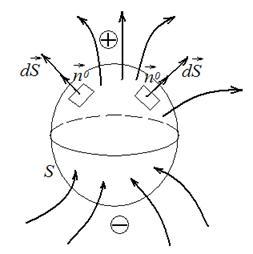 Если рассматриваемая поверхность замкнута, то положительными считаются внешние нормали элементов и потому для всех элементов векторы
Если рассматриваемая поверхность замкнута, то положительными считаются внешние нормали элементов и потому для всех элементов векторы  направлены наружу (рис. 45). Тогда потоки, выходящие из замкнутой поверхности, будут положительными, а входящие потоки – отрицательными.
направлены наружу (рис. 45). Тогда потоки, выходящие из замкнутой поверхности, будут положительными, а входящие потоки – отрицательными.
|
 .
.
3. Определим понятие «дивергенция векторного поля в точке».
|
 Рассмотрим в области задания векторного поля произвольную точку А. Выберем в окрестности этой точки малую замкнутую поверхность dS, ограничивающую объем dV (рис. 46). Найдем поток векторного поля через поверхность dS и разделим его на соответствующий объем dV. Предел этого отношения при стягивании объема dV в точку А называется дивергенцией поля в данной точке:
Рассмотрим в области задания векторного поля произвольную точку А. Выберем в окрестности этой точки малую замкнутую поверхность dS, ограничивающую объем dV (рис. 46). Найдем поток векторного поля через поверхность dS и разделим его на соответствующий объем dV. Предел этого отношения при стягивании объема dV в точку А называется дивергенцией поля в данной точке:
 .
.
|
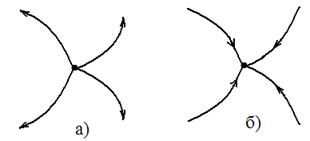 Дивергенция характеризует расходимость и сходимость линий поля в окрестности точки: если дивергенция поля в точке положительна, то картина поля имеет вид, изображенный на рис. 47, а). Такие точки называются источниками поля. Если дивергенция отрицательна, то картина соответствует рис. 47, б) и такие точки называются стоками поля. Иначе говоря, дивергенция характеризует интенсивность (обильность) источников и стоков поля.
Дивергенция характеризует расходимость и сходимость линий поля в окрестности точки: если дивергенция поля в точке положительна, то картина поля имеет вид, изображенный на рис. 47, а). Такие точки называются источниками поля. Если дивергенция отрицательна, то картина соответствует рис. 47, б) и такие точки называются стоками поля. Иначе говоря, дивергенция характеризует интенсивность (обильность) источников и стоков поля.
Дивергенция в декартовой системе координат находится по формуле
 .
.
Пример. В жидкости в местах, где div v ¹0,находятся или ее источники с интенсивностью, равной div v, или стоки жидкости.
4. Определим понятие «вектор элемента длины».
|
 В области задания векторного поля выберем кривую L и на ней выберем положительное направление (рис. 48). Рассмотрим малый элемент линии длиной dl. Введем единичный вектор касательной
В области задания векторного поля выберем кривую L и на ней выберем положительное направление (рис. 48). Рассмотрим малый элемент линии длиной dl. Введем единичный вектор касательной  (
( =1), совпадающий с положительным направлением кривой L в области выбранного элемента линии. Образуем вектор
=1), совпадающий с положительным направлением кривой L в области выбранного элемента линии. Образуем вектор  , модуль которого равен длине элемента и который направлен по касательной к кривой в положительном направлении. Такой вектор называется вектором элемента длины.
, модуль которого равен длине элемента и который направлен по касательной к кривой в положительном направлении. Такой вектор называется вектором элемента длины.
5. Определим понятие «циркуляция векторного поля».
Рассмотрим в векторном поле кривую L и введем на ней положительное направление. Разобьем кривую на малые векторные элементы  , составим для каждого элемента скалярное произведение
, составим для каждого элемента скалярное произведение  и проинтегрируем по всей кривой L. Полученный интеграл
и проинтегрируем по всей кривой L. Полученный интеграл

называется криволинейным интегралом вектора  вдоль кривой L или напряжением векторного поля вдоль кривой L.
вдоль кривой L или напряжением векторного поля вдоль кривой L.
Такой интеграл показывает, в какой мере вектор поля  проецируется на элементы
проецируется на элементы  кривой L.
кривой L.
Пример. Если вектор  есть сила, a
есть сила, a  – перемещение, то криволинейный интеграл выражает работу этой силы на участке траектории L.
– перемещение, то криволинейный интеграл выражает работу этой силы на участке траектории L.
 Криволинейный интеграл по замкнутой кривой
Криволинейный интеграл по замкнутой кривой

|
Поля, для которых циркуляция вектора всюду равна нулю, называются безвихревыми. Это возможно, когда в одних частях контура проекции вектора поля положительны, а в других – отрицательны (рис. 49) и общая сумма проекций по всем элементам контура равна нулю.
6. Определим понятие «ротор векторного поля».
 Рассмотрим в векторном поле произвольную точку А и в ее окрестности рассмотрим малый контур DL, ограничивающий площадь D S (рис. 50).
Рассмотрим в векторном поле произвольную точку А и в ее окрестности рассмотрим малый контур DL, ограничивающий площадь D S (рис. 50).
|
 ,приняв за положительную ту нормаль, при наблюдении с конца которой положительное направление обхода соответствует движению против часовой стрелки.
,приняв за положительную ту нормаль, при наблюдении с конца которой положительное направление обхода соответствует движению против часовой стрелки.
Рассмотрим циркуляцию поля по контуру DL. Очевидно, что величина и знак циркуляции зависят от ориентации контура по отношению к полю. Находим такую ориентацию, при которой циркуляция максимальна по величине и положительна по знаку. Вектор нормали в такой ориентации обозначим  .
.
Предел отношения циркуляции по контуру к площади, ограниченной этим контуром, при стягивании контура DL в точку А

называется ротором поля в точке А. Ротор вектора можно вычислить так:
 .
.
Символический определитель «раскрывается» по первой строке.
О ситуации, когда циркуляция поля по контурам в малой окрестности точки отлична от нуля, говорят как о завихренности поля в окрестности этой точки. Тогда модуль вектора  характеризует степень завихренности векторного поля
характеризует степень завихренности векторного поля  . Направлен этот вектор по нормали к плоскости, в которой имеет место максимальная завихренность, причем так, что при наблюдении с конца вектора завихренность направлена против часовой стрелки.
. Направлен этот вектор по нормали к плоскости, в которой имеет место максимальная завихренность, причем так, что при наблюдении с конца вектора завихренность направлена против часовой стрелки.
Пример. В гидродинамике ротор вектора скорости частиц жидкости отражает наличие у них вращательного движения с некоторой угловой скоростью.
7. Рассмотрим безвихревые и соленоидальные поля.
Если в векторном поле есть контуры с отличной от нуля циркуляцией, то в этом поле обязательно есть точки с отличным от нуля ротором. И, наоборот, в полях, в которых отсутствуют контуры с отличной от нуля циркуляцией, нет и точек с отличным от нуля ротором. Такие поля являются безвихревыми. Следовательно, условия безвихревого характера поля записываются в виде:
 .
.
Первое из них называется дифференциальным условием, а второе – интегральным условием безвихревого характера поля.
Векторные поля, в которых отсутствуют источники и стоки, называются соленоидальными полями. Наиболее распространены такие виды соленоидальных полей, линии которых либо замкнуты, либо обоими концами уходят в бесконечность. Очевидно, что поток соленоидального поля через любую замкнутую поверхность равен нулю, поскольку всякая вошедшая внутрь поверхности линия поля должна из нее выйти. Поэтому условие соленоидальности поля может быть записано в двух формах – в дифференциальной и интегральной:
 .
.
Если в качестве контура взять любую из замкнутых линий соленоидального поля, то, очевидно, циркуляция поля по такому контуру будет отлична от нуля. Следовательно, соленоидальное поле обязательно является вихревым. Но обратное утверждение неверно: вихревое поле вовсе не обязательно будет соленоидальным, ибо существование завихренностей не связано с обязательной замкнутостью линий поля.
8. Математические формулы Гаусса-Остроградского и Стокса.
Согласно формуле Гаусса-Остроградского, поток вектора  через произвольную замкнутую поверхность Sравен интегралу от дивергенции этого вектора, взятому по объему V, ограниченному рассматриваемой поверхностью:
через произвольную замкнутую поверхность Sравен интегралу от дивергенции этого вектора, взятому по объему V, ограниченному рассматриваемой поверхностью:  .
.
Согласно теореме Стокса, циркуляция вектора  по замкнутой кривой равна потоку ротора этого вектора через поверхность S, опирающуюся на кривую L:
по замкнутой кривой равна потоку ротора этого вектора через поверхность S, опирающуюся на кривую L:  .
.
Приложение 6
Не нашли, что искали? Воспользуйтесь поиском: