Коэффициент экономической эффективности производства определяет, сколько производится продукции на один рубль приведенных затрат

КЭ=

1-й год: КЭ =

2-й год: КЭ =

3-й год: КЭ =

17.Удельные совокупные приведенные затраты показывают, сколько рублей приведенных затрат приходится на один рубль ВП:

С =

1-й год: С =

2-й год: С =

3-й год: С =

18. Годовой экономический эффект роста эффективности определяется по формуле:

Э =(С - С )ВП

2-й год: Э =(0,712 – 0,732)43500= - 870 т.руб.

3-й год: Э =(0,682 – 0,712)45700 = - 1371 т.руб.

19.Прирост ВП за счет интенсификации производства находится по следующей формуле:

∆ВП

2-й год: ∆ВП =(1,404 – 1,366)30972= 1176,9 т.руб.

3-й год: ∆ВП =(1,466 – 1,404)31167,4 =1932,4 т.руб.

20.Доля ∆ВП в общем приросте продукции показывает,за счет скольких процентов прирост валовой продукции получен интенсивным способом:

2-й год: %∆ВП =

3-й год: %∆ВП =

21.Совокупная экономическая эффективность от НТП определяется по формуле:

Э =∆ВП

2-й год: Э = 1176,9 –(-870)=2046,9 т.руб.

3-й год Э =1932,4 – (-1371) = 3303,4 т.руб.

22.Индексы:

22.1 Объем продукции: i =

2-й год: i =

3-й год i =

22.2Совокупность приведенных затрат: iс=

2-й год: iс=

3-й год iс=

22.3 Уровень экономической эффективности: i =

2-й год: i =

3-й год i =
22.4.Соотношение индексов эффективности и затрат: d=

2-й год: d =

3-й год d=

24. А) Если бы ∆ВП был обеспечен только за счет расширения производства, то потребовалось бы капиталовложений:КВ=∆ВП*2,5

2-й год:КВ = 4900*2,5=12250 т.руб.

3-й год:КВ = 2200*2,5=5500 т.руб.

Б) Т.К. прирост ВП получен за счет интенсивного и экстенсивного факторов, то фактически для обеспечения всего прироста ВП потребовалось средств на сумму: ∆ВП = 2,5∆ВП + 1,25∆ВП , где ∆ВП =(С - С )КЭ

2-й год: ∆ВП =(30972- 28255,2)1,366 = 3711 т.руб.

∆ВП =2,5*3711 + 1,25*1176,9 = 10748,6 т.руб.

3-й год: ∆ВП = (31167,4 – 30972)1,404 = 274 т.руб.

∆ВП = 2,5*274 + 1,25*1932,4 = 3100,5 т.руб.

В) В итоге экономия на КВ в результате НТП составила: Э =КВ - ∆ВП

2-й год: Э = 12250 – 10748,6 = 1501,4 т.руб.

3-й год: Э = 5500 – 3100,5 = 2399,5 т.руб.

Г) сумма экономии, если К =1,25, позволяет произвести продукции:

- на сумму:

2-й год: 1501,4: 1,25 = 1201,12 т.руб.

3-й год: 2399,5: 1,25 = 1919,6 т.руб.

- в % к объему ВП за год:

2-й год: % =

3-й год:% =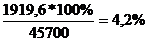

Рис.6. Графическое представление задачи

Пример 2.

Имеется 150 л жидкости А и 150 л жидкости Б.Для получения одной бутыли смеси 1 нужно взять 2л жидкости А и 1л жидкости Б, а для получения одной бутыли смеси 2 нужно взять соответственно 1л жидкости А и 4- жидкости Б.Смесь 1 продается по цене 2 ден.ед., а смесь 2- 3 ден.ед.за одну бутыль. Сколько нужно приготовить бутылей каждой смеси, чтобы их общая стоимость была наибольшей, при условии, что число бутылей со смесью 2 не менее числа бутылей со смесью 1?

Задание 1

Сформулировать экономико-математическую модель исходной экономической задачи.

Введем следующие обозначения: x -количество бутылей первой смеси; x - количество бутылей второй смеси. Стоимость бутылей первой смеси составляет 2x ден.ед.. а второй смеси- 3x ден.ед., т.е. необходимо максимизировать целевую функцию:

F()=2x +3x →max.

Ограничения задачи имеют вид:

x ≥ 0;

Задание 2.

Решить полученную задачу линейного программирования графическим методом.

Прямые ограничения x ≥ 0 означают, что область решений будет лежать в первой четверти декартовой системы координат.

Первое ограничение по жидкости А: 2x +x ≤ 150 Решением этого неравенства является полуплоскость, лежащая ниже прямой 2x +x ≤ 150 (1), проходящей через точки (0;150)и (75;0).

Второе ограничение по жидкости Б: x +4x ≤150. Решением этого неравенства является полуплоскость, лежащая ниже прямой x +4x =150 (2), проходящей через точки (0;37,5) и (150;0).

Получили общую область допустимых решений для всех неравенств ОАВС(Рис.1)

Добавим третье ограничение по количеству бутылей первой и второй смеси x -x 0.Решением неравенства будет являться пересечение прямой x =x (3) c границей области допустимых значений ОАВС, т.е. точка D c координатами (30;30).

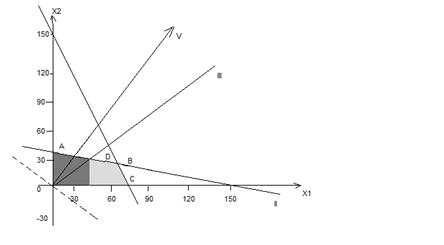Получили новую область допустимых значений:ОАDЕ (Рис.7)

Рис.7. Линейное программирование задач

Построим линию уровня, для чего приравниваем целевую фунцкию к нулю: 2x +3x =0 Линия уровня изображена на рис. 1 пунктирной прямой

Для определения направления движения к оптимуму построим вектор-градиент 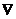, координаты которого являются частными производными целевой функции,.т.е (2;3).Чтобы построить такой вектор, соединяем эту точку с началом координат. В данной задаче движение линии уровня будем осуществлять до её пересечения с точкой D с координатами (30;30); далее она выходит из области допустимых решений. В этой точке достигается максимум целевой функции.

max f()=2*30+3*30=150 ден.ед.и достигается при x =30 и x =30.

Задание 3

Сформулировать двойственную задачу и найти её оптимальное решение, используя теоремы двойственности.

Исходная задача содержит три ограничения: по количеству жидкости А, количеству жидкости Б и количеству бутылей смеси 2.Следоавтельно, в двойственной задаче 3 неизвестных.

y - двойственная оценка жидкости А, или цена жидкости А;

y - двойственная оценка жидкости Б, или цена жидкости Б;

y - двойственная оценка бутылей со смесью 2.

Целевая функция двойственной задачи формулируется на минимум. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи:

g () = 150y +150y +0y → min

Необходимо найти такие цены на y ,y ,y , чтобы общая их стоимость была минимальной.

Число ограничений в системе двойственной задачи равно числу переменных в исходной задаче.В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой фунцкии исходной задачи. Левая часть ограничений определяет стоимость ресурсов, необходимых для получения единицы смеси:

Найдем оптимальный план двойственной задачи, используя теоремы двойственности. Воспользуемся первым соотношением второй теоремы двойственности:

y ,

тогда

Т.к.90<150, то y =0

Воспользуемся вторым соотношением второй теоремы двойственности:

; если x >0, то

В нашей задаче x =30>0 и x =30>0, поэтому ограничения двойственной задачи обращаются в равенства:

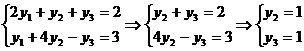
Проверим выполнение первой теоремы двойственности:

g ()=150*0+150*1+0*1=150=f ()

Это означает,что оптимальный план двойственной задачи (0;1;1) определен верно.

Пример 3.

В таблице приведены годовые данные о трудоемкости производства 1 тонны цемента (нормо-смен)

Таблица 2.2.

Исходные данные

Текущий номер года (t)
Трудоемкость 1т цемента (y )	7,9	8,3	7,5	6,9	7,2	6,5	5,8	4,9	5,1	4,4

Задание 1.Сгладить временной ряд методом простой скользящей средней, выбрав длину интервала сглаживания m=3; результаты отразить на графике.

y(2)= y(6)=

y(3)= y(7)=

y(4)= y(8)=

y(5)= y(9)=

y(1) и y(10) не существует.

График результатов сглаживания

Рис.8. Линейное программирование задания

Задание 2. Определить наличие тренда во временном ряду методом Фостера-Стьюарта. Табличные значения статистики t принять равными при уровне значимости α = 0,05 t = 2,23, а при α = 0,3- t = 1,09; другие необходимые табличные значения приведены в таблице 2.3.

Таблица 2.3

Расчетные данные

t
y	7,9	8,3	7,5	6,9	7,2	6,5	5,8	4,9	5,1	4,4
k	-
l	-
S	-
d	-		-1	-1		-1	-1	-1		-1

S=

d =

t > t и t >t , следовательно, можно утверждать с вероятностью 0,95, что тренд есть.

Задание 3.

Для исходного временного ряда построить линейную трендовую модель

, оперделив её параметры на основе метода наименьших квадратов.

Таблица 2.4

Расчетные данные

Показатели	n	Сумма
t
y	7,9	8,3	7,5	6,9	7,2	6,5	5,8	4,9	5,1	4,4	64,5
t²
y t	7,9	16,6	22,5	27,6			40,6	39,2	45,9		319,3
	8,385	7,955	7,525	7,095	6,665	6,235	5,805	5,375	4,945	4,515

Для полинома первой степени система нормальных уравнений имеет вид:

=8,815-0,430t

Задание 4

Оценить адекватность построенной модели на основе исследования:

а) близости математического ожидания остаточной компоненты (ряда остатков) нулю; критические значения t- критерия принять равным тому числу, как указано в задании 2;

б) случайности отклонений остаточной компоненты по критерию пиков (поворотных точек);

в) независимости уровней ряда остатков (отсутствие автокорреляции) на основе критерия Дарбина-Уотсона, используя в качестве критических значений d1=1,08 d2=1,36;

г) нормальности закона распределения уровней остаточной компоненты на основе RS-критерия; в качестве критических значений принять интервал от 2,7 до 3,7.

Таблица 2.5

Показатели	n	Сумма
t
y	7,9	8,3	7,5	6,9	7,2	6,5	5,8	4,9	5,1	4,4	64,5
	8,385	7,955	7,525	7,095	6,665	6,235	5,805	5,375	4,945	4,515
	-0,49	0,345	-0,03	-0,2	0,535	0,265	-0,01	-0,48	0,155	-0,12	-0,03
Точки пиков (р)	-									-
	0,24	0,12	0,001	0,04	0,29	0,07	≈0	0,23	0,024	0,014	1,029
	-	0,83	-0,37	-0,17	0,73	-0,27	-0,27	-0,47	0,63	-0,27
()²		0,69	0,14	0,03	0,53	0,07	0,07	0,22	0,4	0,07	2,22
	6,2	4,16	0,4	2,9	7,43	4,08	0,17	9,79	3,04	2,72	40,89

а) проводя проверку равенства (близости) нулю математического ожидания ряда остатков, заметим, что по результатам вычислений в таблице это математическое ожидание равно(-0,03):10=-0,003 и, следовательно, можно подтвердить выполнение данного свойства, не прибегая к статистике Стьюдента.

Б)проверку случайности уровней ряда остатков проведем на основе критерия пиков (поворотных точек) p >

=

5>

5>2,978, т.е. неравенстов выполняется.Следовательно, можно сделать вывод. Что свойство случайности ряда остатков подтверждается.

В) Для проверки независимости уровней ряда остатков (отсутствие автокорреляции) вычислим значений Дарбина-Уотсона.

Полученная величина 2,16 входит в промежуток от 2 до 4, что свидетельствует об отрицательной автокорреляции, поэтому критерий Дарбина-Уотсона необходимо преобразовать: Данное значение сравниваем с двумя критическими табличными значениями критерия (d1=1,08, d2=1,36): 1,36<1,84<2. Так как расчетное значение попадает в интервал от d2 до 2, то делаем вывод о независимости уровней остаточной последовательности.

Г)Для проверки соответствия остаточной последовательности нормальному закону распределения воспользуемся RS-критерием.

Размах вариации: R=

S =

Критерий RS=1,025: 0,388=3,03

2,7< 3,03< 3,7 => свойство нормальности распределение выполняется

Задание 5.

Оценить точность построения трендовой модели, используя показатели среднего квадратического отклонения от линии тренда и средней относительно ошибки аппроксимации(k=1)

Стандартаня (средняя квдратическая) ошибка оценки прогнозируемого показателя S определяется по формуле:

Средняя относительная ошибка аппроксимации:

ошибка менее 5% говорит о достаточно высоком уровне точности построенной модели.

Задание 6

Построить точечный и интервальный прогноз производства 1т цемента на два шага вперед. Результаты моделирования и прогнозирования отразить на графике

Точечные прогнозы получим, подставляя в уравнение модели значения t=11 и t=12:

Расчет доверительных интервалов по формуле:

U

Для t=11(L=1) K=1,692; t=12 (L=2) K=1,774

Таблица прогнозных значений:

Таблица 2.6

Прогнозные значения

Время (t)	Шаг(L)	Точечный прогноз ()	Доверительный интервал прогноза
Нижняя граница	Верхняя граница
		4,085	3,513	4,657
		3,655	3,055	4,255

U =4,085+0,388*1,692=4,657

U =4,085- 0,388*1,692=3,513

U =3,655+0,388*1,774=4,255

U =3,655- 0,388*1,774=3,055

График результатов моделирования и прогнозирования

Задача стр 7

Рис.9. Линейное программирование задания

 

 

Пример 4. Решить задачу линейного программирования симплексным методом:

Найти наибольшее значение функции f(x)=3x+2x² при ограничениях:

x

 

Приведем эту задачу к каноническому виду, введя дополнительные переменные x ,x , 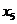со знаком « +» для ограничения «≤» и со знаком «–«для ограничения «≥».

Предварительный анализ показал, что в базис выводится только x , а при выводе других переменных значения свободных членов становятся отрицательными, что не допускается.Тогда для 2-го и 3-го уравнений введем искусственные переменные y и y , которые в дальнейшем будем использовать как базисные переменные.С этой целью введем эти переменные и в целевую функцию:

max f( =3x +2x +0x -M(y +y ),

где М- достаточно большое положительное число

 

Дальнейшее решение приводим в симплекс-таблицах

Таблица 2.7

Расчетные данные

 

№симпл табл.	базис	Сj	План В						-М	-М	Q
Сi	A1	A2	A3	A4	A5	P1	P2
	A3 ←P1 P2	-M -M			-1		-1	-1			5\2
∆j=zj-cj	F = -19M	-3M-3	-2M-2		M	M
|	A3 →A1 ←P2	-M	17\2 5\2 23\2		5\2 -1\2 7\2		1\2 -1\2 1\2	-1			17\5   23\7
∆j=zj-cj	F = 7,5-11,5M		-3,5-3,5M		-3\2-1\2M	M
||	←A3 A1 →A2		2\7 29\7 23\7				1\7 -3\7 1\7	5\7 -1\7 -2\7
∆j=zj-cj	F = 19				-1	-1
	→A4 A1 A2					-1		-1
∆j=zj-cj	F = 21

 

x , x , x , x =0

Задача обладает исходным опорным планом:(0;0;11;0;0;5;14)

F()=0*11+(-M)*5+(-M)*14=-19M

∆ =0*1+(-М)*2+(-М)*1-3=-3М-3

∆ =0*2+(-М)*(-1)+(-М)*3-2=-2М-2

∆ =0*1+(-М)*0+(-М)*0-0=0

∆ =0*0+(-М)*(-1)+(-М)*0-0=М

∆ =0*0+(-М)*0+(-М)*(-1)-0=М

∆ =0*0+(-М)*1+(-М)*0-(-М)=0

∆ =0*0+(-М)*0+(-М)*1-(-М)=0

Q=min(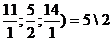

Исходный опорный план не является оптимальным планом, так как среди оценок ∆ имеются отрицательные оценки. В начальной таблице наименьшее ∆ соответствует вектору А - он вводится в базис, а искусственный вектор P из базиса выводится, так как ему отвечает наименьшее Q = 5\2. Столбец, соответствующий P , из дальнейших симплексных таблиц вычеркивается.

x =0

 

Таблица |:

Опорный план:(5\2;0;17\2;0;0;23\3)

F()=0*17\2+3*5\2+(-M)*23\2=7,5-11,5M

∆ =0*0+3*1+(-М)*0-3=0

∆ =0*5\2+3*(-1\2)+(-М)*7\2-2=3,5-3,5М

∆ =0*1+3*0+(-М)*0-0=0

∆ =0*1\2+3*(-1\2)+(-М)*1\2-0=-3\2-1\2М

∆ =0*0+3*0+(-М)*(-1)-0=М

∆ =0*0+3*0+(-М)*1-(-М)=0

Q= min(

Опорный план таблицы 1не является оптимальным планом, так как среди оценок ∆ имеются отрицательные оценки. В таблице 1 наименьшее ∆ соответствует вектору А - он вводится в базис, а искусственный вектор P из базиса выводится, так как ему отвечает наименьшее Q = 23\7. Столбец, соответствующий P , из дальнейших симплексных таблиц вычеркивается.

x =0

Таблица 2:

Опорный план: (29\7;23\2;2\7;0;0)

F()=0*2\7+3*29\7+2*23\7=133\7=19

∆ =0*0+3*1+2*0-3=0

∆ =0*0+3*0+2*1-2=0

∆ =0*1+3*0+2*0-0=0

∆ =0*1\7+3*(-3\7)+2*1\7-0=-1

∆ =0*5\7+3*(-1\7)+2*(-2\7)-0=-1

Q= min(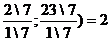

Опорный план таблицы 2 не является оптимальным планом, наименьшее ∆ соответствует вектору А и А . Сначала выбираем вектор А - он вводится в базис, а вектор А из базиса выводится, так как ему отвечает наименьшее Q = 2.

x =0

Таблица 3:

Опорный план:(5;3;0;2;0)

F()=0*2+3*5+2*3=21

∆ =0*0+3*1+2*0-3=0

∆ =0*0+3*0+2*1-2=0

∆ =0*7+3*3+2*(-1)-0=7

∆ =0*1+3*0+2*0-0=0

∆ =0*5+3*2+2*(-1)-0=4

Опорный план таблицы 3 является оптимальным планом для исходной задачи. Для него все ∆ ≥ 0,поэтому он является оптимальным. Таким образом, получен оптимальный план исходной задачи (5;3), и максимальное значение целевой функции f( =21.

 

Пример 5. Предприятие «Кронос» занимается производством резиновых изделий. В будущем году оно хотело бы расширить ассортимент своей продукции и производить резиновые прокладки для смесителей воды. Для этого необходимо провести исследование спроса на данный вид продукции.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.

Простейшей моделью (формулой), выражающей тенденцию развития является

линейная функция – прямая

у_t = а₀ + а₁∙t,

где y_t - теоретические уровни,

а₀ и а₁ – параметры прямой,

t – показатель времени (дни, месяцы, годы и т.д.).

Для нахождения параметров а₀ и а₁ необходимо решить систему нормальных уравнений

а₀∙n + a₁∑t = ∑y,

a₀∑t + a₁∑t² = ∑yt,

где у – фактические уровни ряда динамики,

n – число уровней.

Для упрощения расчётов обозначим время так, чтобы начало его отсчёта приходилось на середину рассматриваемого периода.

Представим это в таблице.

Таблица 2.8

Расчётные данные для определения параметров системы нормальных уравнений и выравненных теоретических значений.

год	Средний объем спроса (руб.), у	t	t2	y∙t	_ yt
		-2		-3222	1330,4
		-1		-1879	1931,3
					2532,2
					3133,1
Итого:	∑у = 12 661	∑t = 0	∑ t2= 10	∑y∙t = 6009	_ ∑ yt = 12 661

Так как ∑t = 0, то система нормальных уравнений примет вид

а₀∙n = ∑у,

а₁∑t² = ∑yt.

 

Отсюда

∑у ∑уt

а₀ = ——; а₁ = ————

n ∑t²

12 661 6009

а₀ = ———— = 2532,2руб. а₁ = ———— = 600,9руб.

5 10

 

Уравнение прямой будет иметь вид

у_t = 2532,2 + 600,9∙t

Подставив в это уравнение значение t (таблица 2, графа 3), получим выровненные теоретические значения (таблица 2, графа 6).

_

у_t1 = 2532,2 + 600,9∙(-2) = 1330,4руб.

_

у_t2 = 2532,2 + 600,9∙(-1) = 1931,3руб.

_

у_t3 = 2532,2 + 600,9∙0 = 2532,2руб.

_

у_t4 = 2532,2 + 600,9∙1 = 3133,1руб.

_

у_t5 = 2532,2 + 600,9∙2 = 3734руб.

 

Полученное уравнение показывает, что, несмотря на колебания в отдельные годы, наблюдается тенденция увеличения объема спроса на резиновые прокладки для смесителей воды: с первого по пятый годы спрос увеличивался в среднем на 600,9 рублей в год. Поэтому можно предположить, что в ближайшем году спрос увеличится на 600,9 рублей.

Динамику спроса можно представить в графическом виде.

 

 

- выравненные уровни спроса

- эмпирические уровни спроса

 

Рис.10. Линейное программирование задачи

 

Список литературы

1. Голиков, Е.А. Маркетинг и логистика: Учеб. пособие / Е.А.Голиков. - М.: издательский дом «Дашков и К°», 2001. - 412 с,

2. Гусаров, В.М. Статистика: Учеб. пособие / В.М. Гусаров. - М.: ЮНИТИ -ДАНА, 2001. - 463 с.

3. Дайтбергов, Д.М. Основы маркетинга: Практикум / под ред. Д.М. Дайтбергова, И.М. Синяевой. - М.: Вузовский учебник, 2007. - 365 с.

4. Елисеева, И.И. Социальная статистика: Учебник / под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. - 480 с.

5. Кондрашов, В.М.Управление продажами: учеб.пособие для студентов вузов, обучающихся по специальности «Маркетинг» (080111), «Коммерция (торговое дело)» (080301) / В.М. Кондрашов; под ред. В.Я. Горфинкеля. – М.: ЮНИТИ-ДАНА, 2007. – 319с.

6. Кундышева, Е.С. Математическое моделирование в экономике: Учеб. пособие / Е.С. Кундышева. - М.: Издательско-торговая компания «Дашков и К°», 2006. - 352 с.

7. Мурахтанов, Н.М. Маркетинг: Сборник практических задач и ситуаций: Учеб.пособие / Н.М. Мурахметова, Е.И. Еремина. – 2-е изд., стер. – М.: Издательский центр «Академия», 2005. – 96 с.

8. Мартузалиева, Т.В. Маркетинг-практикум: задачи, кейсы, тесты: учебное пособие / Т.В. Муртузалиева, Р.К. Цахаев. – М.: Издательство «Экзамен», 2008. – 287с.

9. Переяслова, И.Г. Статистика для студентов вузов / И.Г. Переяслова, Е.Б. Колбачев, О.Г. Переяслова. - Ростов н/Д.: Феникс, 2005, -219 с.

10. Степнева, Т.А. Цены и ценообразование: Учеб. пособие / Т.А.Степнева, Е.В. Яркин. - М.: ИНФРА-М, 2001. - 240 с.

11. Шелобаев, С.И. Экономико-математические методы и модели: Учеб. пособие / С.И. Шелобаев. - М.: ЮНИТИ - ДАНА, 2005. - 287 с.

12. Шуляк, П.Н. Ценообразование: Учебно-практическое пособие / П.Н. Шуляк. - М.: Издательский дом «Дашков и К°», 2001. - 216 с.

Не нашли, что искали? Воспользуйтесь поиском: