Второе начало термодинамики. Энтропия.

· К. п. д. тепловой машины:

η = A/ Q₁ = 1 – Q₂/Q₁,

где Q ₁ - тепло, получаемое рабочим телом; Q₂ - отдаваемое тепло.

· К.п.д. цикла Карно:

,

где T ₁, T ₂ - температуры нагревателя и холодильника.

· Неравенство Клаузиуса:

где δ Q - элементарное тепло, полученное системой.

· Приращение энтропии системы:

· Основное уравнение термодинамики для обратимых процессов:

T d S = d U + p d V

· Свободная энергия:

F = U - TS, A _T = - Δ F

· Связь между энтропией и статистическим весом Ω (термодинами­ческой вероятностью):

S = k∙ lnΩ,

где k - постоянная Больцмана.

3.1. У тепловой машины, работающей по циклу Карно, температура нагревателя в п = 1,6 раза больше температуры холодильника. За один цикл машина производит работу А = 12 кДж. Какая работа за цикл затрачивается на изотермическое сжатие вещества? (Рабочее вещество - идеальный газ.)

Ответ: А' = А/(п - 1) = 20 кДж.

3.2. В каком случае к.п.д. цикла Карно повысится больше: при увеличении температуры нагревателя на Δ Т или при уменьшении температу­ры холодильника на такую же величину?

Ответ: при уменьшении температуры холодильника Т ₂.

3.3. Водород совершает цикл Карно. Найти к.п.д. цикла, если при адиабатическом расширении:

а) объем газа увеличивается в п = 2,0 раза;

б) давление уменьшается в n = 2,0 раза.

Ответ: a) η = 1 – n^1-γ = 0,25; б) η = 1 – n^1/(γ-1) = 0,18

3.4. Холодильная машина, работающая по обратному циклу Карно, должна поддерживать в своей камере температуру — 10° Спри темпера­туре окружающей среды 20° С. Какую работу надо совершить над ра­бочим веществом машины, чтобы отвести от ее камеры Q₂ = 140 кДж тепла?

Ответ: А' = Q ₂(T _1/ T ₂ - 1) = 16 кДж.

3.5. Тепловую машину. работающую по циклу Карно с к.п.д. η 10% используют при тех же тепловых резервуарах как холодильную машину. Найти ее холодильный коэффициент ε.

Ответ: ε = (1 - η)/η = 9

3.6. Найти к.п.д. цикла, состоящего из двух изобар и двух адиабат, если в пределах цикла давление изменяется в п раз. Рабочее вещество идеальный газ с показателем адиабаты γ.

Ответ: η = 1 – η^{-(γ - 1)/γ.}

3.7. Идеальный газ с показателем адиабаты γ, совершает цикл, со­стоящий из двух изохор и двух изобар. Найти к.п.д. такого цикла, если температура Т газа возрастает в п раз как при изохорическом нагреве, так и при изобарическом расширении.

Ответ: η = 1 – (n + γ)/(1 + γ n).

3.8. Идеальный газ совершает цикл, состоящий из:

а) изохоры, адиабаты и изотермы;

б) изобары, адиабаты и изотермы,

причем изотермический процесс происходит при минимальной тем­пературе цикла. Найти к.п.д. каждого цикла, если температура в его пределах изменяется в п раз.

Ответ: в обоих случаях η = 1 – ln n /(n - 1)

3.9. Идеальный газ с показателем адиабаты γ совершает прямой цикл, состоящий из адиабаты. изобары и изохоры. Найти к.п.д. цикла, если при адиабатическом процессе объем идеального газа:

а) увеличивается в n раз:

б) уменьшается в n раз.

Ответ: a) η = 1 – γ(n – 1)/(n ^γ – 1); б) η = 1 – (n ^γ – 1)/γ(n – 1) n ^γ–1.

3.10. Воспользовавшись неравенством Клаузиуса, показать, что к.п.д. всех циклов, у которых одинакова максимальная температура Т _maxи одинакова минимальная температура Т _min, меньше, чем у цикла Карно при Т _max и Т _min. Указание: Учесть, что неравенство ∫δ Q ₁/ T ₁ - ∫δ Q^′ ₂ /T ₂ ≤ 0 только усиливается при замене Т ₁на Т _max и Т ₂на Т _min.

3.11. Какую максимальную работу может произвести тепловая ма­шина, если в качестве нагревателя используется кусок железа массы m = 100 кг с начальной температурой Т ₁ =1500 К. а в качестве хо­лодильника вода океана с температурой Т ₂ = 285 К?

Ответ: А _max = mc [ T ₁ – T ₂ – T ₂∙ln(T ₁/ T ₂)] = 34 МДж, где с - удельная теплоемкость железа.

3.12. В качестве основных переменных, характеризующих состояние тела, можно принять его температуру и энтропию. Изобразить графиче­ски цикл Карно на диаграмме, откладывая по оси абсцисс энтропию, а по оси ординат температуру. Вычислить с помощью этого графика к.п.д. цикла.

3.13. Найти изменения энтропии моля идеального газа при изохорическом, изотермическом и изобарическом процессах.

3.14. Найти изменение энтропии при переходе 80 г кислорода от объема 10 л при температуре 80^о C к объему в 40 л при температуре 300^о C.

Ответ:

3.15. Один кубический метр воздуха, находящегося при температуре 0^оC и давлении 19,6 Н/cм², изотермически расширяется от объема V ₁ до объема V ₂ = 2 V ₁. Найти изменение эн­тропии при этом процессе.

Ответ:

3.16. Доказать, что энтропия v молей идеального газа может быть представлена в виде: S = v [ c_V ln T + R ln(V / v) + const], где аддитивная постоянная в скобках не зависит от числа частиц газа.

3.17. В двух сосудах одного и того же объема находятся различные идеальные газы. Масса газа в первом сосуде m ₁во втором – m ₂, давление газов и температуры их одинаковы. Сосуды соединили друг с другом, и начался процесс диффузии. Определить суммарное изменение Δ S энтро­пии рассматриваемой системы, если относительная молекулярная масса первого газа μ_1, а второго μ₂.

Ответ: Δ S = R ln2(m ₁/μ₁ + m ₂/μ₂).

3.18. Теплоизолированный цилиндрический сосуд разделен поршнем пренебрежимо малой массы на две равные части. По одну сторону порш­ня находится идеальный газ с массой m, относительной молекулярной массой μ и молярными теплоемкостями C_p и С_v,не зависящими от темпе­ратуры, а по другую сторону поршня создан высокий вакуум. Начальные температура и давление газа T ₀ и p ₀. Поршень отпускают, и он, свободно двигаясь, дает возможность газу заполнить весь объем цилиндра. После этого, постепенно увеличивая давление на поршень, медленно доводят объем газа до первоначальной величины. Найти изменение внутренней энергии н энтропии газа при таком процессе.

Ответ: Δ U = U - U ₀ = (m /η)∙ C_VT ₀(2^γ-1 - 1);

ΔS = S - S ₀ = (m /μ)∙ C_V (γ - 1)ln2.

3.19. Зная зависимость свободной энергии от температуры и объ­ема F(T, V), показать, что давление р = -(дF/дV)_T и энтропия S = -(дF/д T) _V.

3.20. Наряду с внутренней энергией U и свободной энергией F в тер­модинамике широко используют функции Н = U + рV - энтальпию и Ф = F + рV - свободную энергию Гиббса. Доказать, что эти функции удовлетворяют соотношениям:

dU = TdS – pdV,	dF = -SdT – pdV,
d Ф = -SdT + Vdp,	dH = TdS + Vdp,

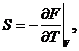
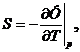
3.21. Доказать соотношения Максвелла:

3.22. В чем ошибочность следующего рассуждения? Элементарное количество тепла dQ,полученное физически однород­ным телом при квазистатическом процессе, равно

dQ = dU + pdV = dH – Vdp,

или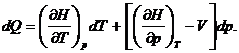

Отсюда

Приравнивая оба выражения, получим (∂ V /∂ T)_p= 0. Отсюда следует, что тепловое расширение тел невозможно.

3.23. Показать, что внутренняя энергия вещества с уравнением состо­яния в форме р = f (V)T не зависит от объема.

3.24. Внутренняя энергия и единицы объема является функцией толь­ко от T, а уравнение состояния газа имеет вид р = и (Т) / 3Определить функциональную форму и (Т).

Ответ: u (T) = const T ⁴ - (фотоновый газ)

3.25. Для идеального электронного газа имеет место соотношение: PV = ²/₃ U. Найти для этого газа уравнение адиабаты: а) в перемен­ных (Р, V); б) в переменных (V, Т).

Ответ: а) РV ^5/3 = const; б) TV ^2/3 = const.

3.26. Показать, что для веществ, у которых давление является линей­ной функцией температуры Т, теплоемкость Сv не зависит от объема.

3.27. Используя соотношения Максвелла найти выражение для энтро­пии моля газа Ван-дер-Ваальса.

Ответ:

3.28. Вычислить плотность энтропии S поля теплового излучения.

Ответ: S =⁴/₃ aT ³+const. (см. задачу 2.32).

3.29. Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.

Ответ:

3.30. Определить температуру смеси CO₂ и H₂, если разность средних кинетических энергий на одну молекулу того и другого газа равна 2,07·10^-14 эрг. Газ считать идеальным.

Ответ: 300^оК.

3.31. N атомов газообразного гелия находятся при комнатной темпе­ратуре в кубическом сосуде объемом 1,0 см³. (Cреднее время пролета атомов гелия расстояния порядка размера сосуда τ ~ 10^-5 c).Найти:

а) вероятность того, что все атомы соберутся в одной половине сосуда;

б) примерное числовое значение N, при котором это событие можно ожидать на протяжении t = 10¹⁰ лет (возраст Вселенной).

Ответ: a) p = ¹/₂^N ; б) N = 1g (t/τ)/ 1g 2 = 80. где

3.32. Найти статистический вес наиболее вероятного распределения N = 10 одинаковых молекул по двум одинаковым половинам сосуда. Определить вероятность такого распределения.

Ответ: Ω _вер = N!/[(N /2)!]²=252, p _N/2 = Ω _вер /2^N = 24,6%.

3.33. Какое количество тепла необходимо сообщить макроскопической системе, находящейся при температуре Т = 290 K, чтобы при неизменном объеме ее статистический вес увеличился на Δη = 0,1%?

Ответ: δ Q = kT Δη = 4·10^-23 Дж.

3.34. Один моль идеального газа, состоящего из одноатомных моле­кул, находится в сосуде при температуре T ₀= 300 K. Как и во сколько раз изменится статистический вес этой системы (газа), если ее нагреть изохорически на Δ T = 1,0 K?

Ответ: Увеличится в Ω/Ω₀ = (1 + Δ T / T ₀) ^iNa/2 = 10^1,31·10ˆ21 раз.

Не нашли, что искали? Воспользуйтесь поиском: