Определение погрешностей при прямых измерениях

Прямыми называют такие измерения, при которых физическая величина измеряется непосредственно при помощи прибора.

Пусть х – действительное значение измеряемой величины, а х₁ – показания прибора. Абсолютной погрешностью называется величина

. (1.1)

Точность измерения характеризуется отношением абсолютной погрешности к действительному значению измеряемой величины

. (1.2)

Это отношение называется относительной погрешностью и выражается в процентах.

Погрешности, допускаемые при прямых измерениях, нередко называются приборными, так как обусловлены классом точности прибора, который указывается либо на самом приборе, либо в паспорте. В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены деления.

Случайные погрешности имеют статистический характер, их математическая обработка производится с помощью теории вероятностей. При многократном измерении равновероятно получить результат как больший, так и меньший, чем истинное значение измеряемой величины.

Пусть проведено n измерений величины х и в результате получено n значений: х₁, х₂, …х_n. Величина

(1.3)

называется средним арифметическим значением, является хорошим приближением к истинному значению измеряемой величины и, как правило, используется как окончательный итог серии измерений.

Рассмотрим несколько основных этапов упрощенной математической обработки результатов измерений.

1. Находим среднее арифметическое значение измеряемой величины

2. Вычисляем абсолютные погрешности результатов отдельных измерений

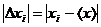
(1.4)

Абсолютная погрешность имеет размерность измеряемой величины и характеризует качество отдельных измерений.

3. Вычисляем среднюю абсолютную погрешность

(1.5)

4. Вычисляем относительную погрешность

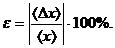(1.6)

5. Записываем окончательный результат . (1.7)

Не нашли, что искали? Воспользуйтесь поиском: