Базисные переменные на каждой итерации можно выбирать различными способами, поэтому запись общего решения может быть разной. Однако, само множество решений одно и то же.

Вернемся к анализу систем уравнений (1) и (1⁰). Если в системах (1) и (1⁰) все соответствующие (с одинаковыми номерами) коэффициенты при переменных совпадают, то системы (1) и (1⁰) называются соответствующими. Множества решений систем (1) и (1⁰) обозначаем X^b и X⁰. Система (1) совместна, если X^b ≠ .

Теорема 3. Если в однородной системе уравнений (1⁰) n > m, то система (1⁰) имеет бесконечное число решений.

Доказательство. Однородная система всегда совместна (набор = (, ,…, ), где 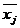= 0 при всехj = 1,…,n, очевидно, является её решением), т.е. X⁰ ≠ . Если решать ее методом Гаусса – Жордана, то он остановится через r итераций и r ≤ min (m,n) = m < n. Тогда число свободных переменных есть n – r ≥ n – m > 0. Отсюда следует, что система имеет бесконечное число решений. Теорема доказана.

Теорема 4. Пусть y = (y₁, y₂, …, y_n) и z = (z₁, z₂, …, z_n) – решения однородной системы (1⁰), т.е. y X⁰, z X⁰. Тогда

1) x* = y + z = (y₁ + z₁, y₂ + z₂, …, y_n + z_n) X⁰,

2) x = y = ( y₁, y₂, …, y_n) X⁰.

Доказательство. 1) Так как y X⁰, z X⁰, то

= 0, i = 1,…,m, = 0, i = 1,…,m. (12)

Проверим, является ли x* решением (1⁰). Для этого рассмотрим . В силу (12)

= = + = 0, т.е. x* X⁰.

2) Так как = = 0, то x = y X⁰. Теорема доказана.

Рассмотрим теперь соответствующие друг другу системы (1) и (1⁰). Пусть система (1) совместна, т.е. X^b ≠ . Пусть = (, ,…, ) – некоторое фиксированное частное решение системы (1), т.е. = b_i при всех i = 1,…,m.

Теорема 5. Пусть система (1) совместна и = (, ,…, ) – некоторое её фиксированное частное решение. Тогда

1) произвольное решение x = (x₁, x₂, …, x_n) является суммой (почленной) этого фиксированного решения и некоторого решения z = (z₁, z₂, …, z_n) соответствующей однородной системы;

2) если z = (z₁, z₂, …, z_n) – произвольное решение однородной системы (1⁰), то x = + z = ( + z₁, + z₂,…, + z_n) – решение соответствующей неоднородной системы (1).

Доказательство. 1) Так как X^b и x X^b,то

= b_i, = b_i при всех i = 1,…,m. (13)

Построим набор z = (z₁, z₂, …, z_n)следующим образом:

z_j = - x_j, j = 1, …, n. (14)

Покажем, что z – решение соответствующей однородной системы. Действительно, в силу (14) и затем (13)

= = - = b_i - b_i = 0.

Так как это верно для любого i = 1,…,m, то набор z, определенный в (14), является решением системы (1⁰).

2) Пусть z = (z₁, z₂, …, z_n) X⁰, т.е.

= 0 при всех i = 1,…,m. (15)

Положим

x_j = + z_j, j = 1, …, n. (16)

Покажем, что x = (x₁, …, x_n) – решение системы (1). Из (16), (13) и (15) следует

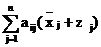= = + = b_i + 0 = b_i при всех i, т.е. x X^b. Теорема доказана.

Теорема 5 утверждает, что для того, чтобы найти все решения системы (1), достаточно найти одно её решение и все решения соответствующей однородной системы (1⁰).

Это всё, что мы пока можем сказать о системе из m линейных уравнений с n переменными. Будем возвращаться к анализу таких систем во всех следующих темах.

Не нашли, что искали? Воспользуйтесь поиском: