4 страница. Система л.н. не компланарны, т.е

Система л.н. не компланарны, т.е. не лежат в одной плоскости (в трехмерном случае это надо понимать буквально, в n -мерном – следует говорить о двумерной плоскости, которую мы пока будем понимать интуитивно).

Вообще, линейная независимость – это некоторое свойство общего положения: паре не быть коллинеарной, тройке не быть компланарной и т.д. «Малым шевелением» векторов л.н. нельзя «разрушить», в то время как зависимость (коллинеарность, компланарность...) – можно.

Система векторов

называется ортогональной, если все они ненулевые и

для всех ,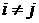

т.е. различные векторы попарно ортогональны.

Утверждение. Ортогональная система линейно независима.

Докажите это утверждение от противного.

Линейно независимая система называется базисом в Rⁿ, если всякий вектор в Rⁿ является линейной комбинацией векторов этой системы.

Можно доказать, что любой базис в Rⁿ состоит ровно из n элементов и любая линейно независимая система из n элементов является базисом в Rⁿ.

Лекция 7.

Тема: Линейная алгебра (продолжение)

3. Разложение вектора по базису.

Пусть – базис в Rⁿ. Тогда всякий вектор можно разложить по базису, то есть представить в виде линейной комбинации элементов базиса:

.

Лемма. Разложение по базису единственно.

Доказательство. Пусть есть другое разложение:

.

Вычтем отсюда

.

Получим

.

В силу линейной независимости векторов базиса имеем:

,

т.е. все коэффициенты совпадают. n

Коэффициенты разложения вектора в данном базисе называют также координатами его в данном базисе.

Рассмотрим систему

.

Она ортогональна и, следовательно, линейно независима. Поскольку элементов n, то это – базис. Он называется стандартным, или каноническим базисом Rⁿ. Разложение вектора

в этом базисе выглядит особенно просто:

,

т.е. координаты вектора в этом базисе совпадают с его собственными координатами (компонентами). Конечно, для других базисов это будет, вообще говоря, не так.

Отметим, что

.

Благодаря этому базис е ₁,..., е_n называют нормированным. Поскольку он еще ортогональный, то его называю ортонормированным. Это – аналог и обобщение системы координатных ортов 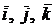, к которым мы привыкли в векторной алгебре.

Приведем пример другого базиса в Rⁿ:

.

Докажите линейную независимость системы .

4. Подпространство.

Введем еще одно важное понятие – подпространство.

Определение. Множество 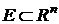называется подпространством, если:

1) сумма любых двух векторов из Е снова принадлежит Е;

2) произведение любого вектора из Е на скаляр есть вектор из Е.

Итак, операции сложения и умножения на скаляр не выводят за пределы подпространства, и это свойство является определяющим для подпространства. Говорят еще, что подпространство замкнуто относительно операций сложения и умножения на скаляр.

Важный пример подпространства следующий: пусть 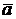– ненулевой вектор в Rⁿ, рассмотрим множество

– гиперплоскость, состоящую из векторов, ортогональных вектору 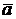. Проверьте, что это множество есть подпространство.

Множество

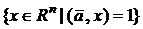
также называется гиперплоскостью в Rⁿ, но подпространством уже не является хотя бы потому, что не содержит нуля (а почему всякое подпространство содержит ноль?). Вообще гиперплоскость определяется равенством и является подпространством лишь в случае, когда . В этом случае гиперплоскость называют нулевой.

Очевидно, множество состоящее из нулевого вектора есть подпространство в Rⁿ и все Rⁿ есть подпространство самого себя. Эти два подпространства называют несобственными. Какие собственные пространства имеются в R ³ –? Это прямые и плоскости, проходящие через начало координат. Других нет. Заметим, что пересечение двух и более подпространств есть подпространство. Например, система условий

определяет подпространство в Rⁿ.

Базис подпространства определяется точно так же как базис в Rⁿ.

Пусть 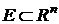– подпространство. Система линейно независимых векторов в Е называется базисом в Е, если любой
вектор из Е представим в виде линейной комбинации векторов .

Доказывается, что все базисы подпространства состоят из одного и того же числа векторов m, которое называется размерностью Е и обозначается dim Е (от слова dimension – размерность).

Рассмотрим R ³.

Векторы вида образуют двумерное подпространство (ортогональное вектору (0,0,1)) с базисом

.

Приведите менее тривиальный пример подпространства и базиса
в R ³.

5. Произведение матрицы на вектор.

Таблица из m строк и n столбцов чисел называется прямоугольной матрицей порядка m ´ n:

.

Отметим, что a_ij – элемент i -й строки и j -го столбца.

Матрица называется квадратной, если . С квадратными матрицами мы уже имели дело.

Пусть наряду с матрицей А порядка m ´ n имеется вектор

.

Их произведением Ах называется вектор

,

координаты которого вычисляются по формулам:

Таким образом, первая компонента вектора Ах есть скалярное произведение первой строки

матрицы А на вектор х, вторая компонента вектора Ах – произведение второй строки

на вектор х и т.д. Коротко можно записать:

.

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными

,

с матрицей А, вектором неизвестных х и вектором правых частей

.

Используя умножение матрицы на вектор, систему можно коротко записать в виде:

.

Наша ближайшая цель – научиться решать такие системы, т.е. описывать все множество решений. Одно из важнейших понятий, которые мы будем при этом использовать – понятие «ранга системы векторов» и связанное с ним понятие «ранга матрицы». Научившись находить ранг, мы быстро научимся решать системы.

Лекция 8.

Тема: Приведение матрицы к ступенчатому виду

1. Ранг системы векторов.

Пусть даны векторы

(*)

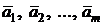в пространстве Rⁿ.

Рангом системы векторов (*) назовем максимальное число линейно независимых векторов этой системы.

Пример. Рассмотрим векторы

, , ,

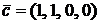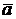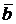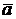в пространстве R ⁴. Каков ранг этой системы? Ясно, что и линейно независимы (например, потому, что они ортогональны). Кроме того, , т.е. и есть линейные комбинации векторов и 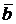. Значит, линейно независимая подсистема максимальна, откуда вытекает, что ранг системы равен двум. Однако часто бывает трудно непосредственно обнаружить максимальную линейно независимую подсистему, которую называют базисом данной системы, и тем самым определить ранг. Сейчас мы изучим стандартную процедуру, позволяющую находить ранг любой системы. Она называется методом
Гаусса.

Дадим еще определение ранга матрицы. Пусть дана матрица

.

Горизонтальным рангом матрицы A называется ранг системы
ее строк

Вертикальным рангом матрицы называется ранг системы ее столбцов

.

Несколько неожиданный факт состоит в том, что у любой матрицы горизонтальный и вертикальный ранги всегда совпадают. Их общее значение называется рангом матрицы А и обозначается rank А.

Другое определение (эквивалентное): ранг матрицы равен наивысшей размерности отличного от нуля минора. При этом минором порядка k называется определитель матрицы, расположенной на пересечении произвольных k строк и k столбцов матрицы А.

Перейдем к описанию процедуры вычисления ранга матрицы (а значит и ранга системы векторов, ибо одно непосредственно связано с другим).

2. Приведение матрицы к ступенчатому виду.

Ступенчатый вид матрицы указан на картинке:

Белое поле – это нули. Квадратики с густой штриховкой – ненулевые элементы: . Поле с редкой штриховкой – произвольные элементы (нули или не нули – все равно).

Элемент назовем угловым, если он отличен от нуля, а всюду левее и ниже него все элементы – нули (на рисунке угловые элементы – ).

Ступенчатый вид характеризуется тем, что первые r строк содержат угловые элементы, а остальные строки (если ) – нулевые.

Подчеркнем, что «высота» ступеньки всегда единица, а ширина – произвольна.

Утверждение. Пусть матрица имеет ступенчатый вид. Тогда ее ранг равен числу угловых элементов.

Линейная независимость строк, содержащих угловые элементы, почти очевидна. На этом основано доказательство данного утверждения (которое мы опускаем).

Возникает вопрос: нельзя ли с помощью преобразований, не меняющих ранга, привести произвольную матрицу к ступенчатому виду и, таким образом, вычислить ранг? Оказывается, можно. Опишем эти преобразования, которые будем называть элементарными:

(1) перестановка строк;

(2) к одной строке прибавляется другая строка, умноженная на число.

Эти преобразования не меняют ранга.

Теорема. С помощью элементарных преобразований (1) и (2) любую матрицу можно привести к ступенчатому виду.

Опишем, как это делается. Будем считать, что первый столбец ненулевой (если это не так, находим первый ненулевой столбец и всю процедуру применяем к той части матрицы, которая располагается правее этого столбца и включает его:

Перестановкой строк (если потребуется) добиваемся, чтобы первый элемент первой строки был отличен от нуля. Итак, не ограничивая общности, считаем, что . Далее с помощью преобразований (2), используя 1-ю строку, добиваемся, чтобы все коэффициенты, расположенные ниже коэффициента а ₁₁, оказались нулями. При этом 1-ю строку сохраняем:

Конкретно: из 2-й строки вычитаем первую, умноженную на . Тогда на месте первого элемента второй строки а ₂₁ окажется ноль. Так же поступаем с 3-й, 4-й и т.д. строками. В результате ниже а ₁₁ получаем нули, т.е. приходим к виду, указанному на рисунке.

Матрица А ¢, расположенная ниже первой строки и левее первого столбца, имеет на одну строку и на один столбец меньше, чем А. Для нее повторяем те же операции. Через конечное число шагов (не превышающее m) приходим к ступенчатому виду. Указанная процедура носит название «прямой ход метода Гаусса».

Пример: вычислить ранг матрицы

.

Третья строка есть сумма первых двух, а четвертая – их разность. Поэтому ранг равен 2 (первые две строки не пропорциональны и поэтому линейно независимы). Сделаем вид, что мы «не знаем ответ». Найдем его с помощью метода Гаусса.

Элемент а ₁₁ равен 1, что, конечно, очень удобно. Первую строку сохраняем. Вторую преобразовываем так: первую умножаем на 2 и вычитаем из второй. Результат записываем во вторую. Это действие запишем коротко так:

,

т.е. вторая строка переходит в разность: вторая минус первая, умноженная на 2. Аналогично

, .

В результате первого шага получаем

.

На втором шаге с помощью второй строки добиваемся нулей ниже элемента :

, .

В результате получаем:

.

Матрица имеет ступенчатый вид. Угловых элементов, а значит, и ступенек, две. Следовательно rank А = 2.

Лекция 9.

Тема: Системы линейных алгебраических уравнений

1. О совместности системы.

Рассмотрим систему m уравнений с n неизвестными:

(1)

Положим

.

Как уже говорилось, A – матрица системы, х – неизвестный вектор, b – вектор правых частей.

Коротко:

– матрично-векторная запись системы. Система, имеющая хотя бы одно решение х, называется совместной, в противном случае – несовместной.

Положим

– столбцы матрицы А. Тогда систему можно записать в виде:

.

Из этой записи видно, что решить систему – значит представить вектор b как линейную комбинацию столбцов А ₁,..., А_n матрицы А, причем, х ₁,..., х_n – коэффициенты этой линейной комбинации. Это представление возможно, если добавление вектора b к столбцам А ₁,..., А_n не повышает ранга системы столбцов. Значит, совместность системы (1) эквивалентна тому, что расширенная система { А ₁,..., А_m, b } имеет тот же ранг, что и система { А ₁,..., А_m }.

Сформулируем то же самое на языке матриц. Введем матрицу

,

т.е. добавим к А столбец b.

Назовем расширенной матрицей. Из сказанного выше вытекает:

Теорема 1 (Кронекера–Капелли). Система (1) совместна тогда и только тогда, когда (т.е. ранги матрицы системы и расширенной матрицы системы совпадают).

2. Однородная и неоднородная системы.

Если , система (1) называется неоднородной. Соответствующая однородная система имеет вид:

(2)

или, коротко

.

Заметим, что однородная система всегда совместна, поскольку

– ее решение.

Вопрос лишь в том, единственно ли это решение, и если нет, то что собой представляет множество всех решений?

Теорема 2. Множество всех решений однородной системы представляет собой подпространство в Rⁿ.

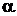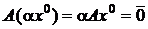Доказательство. Если х ⁰ – решение, т.е. , и – число, то – тоже решение, ибо . Кроме того, если х ¹ и х ² – решения, т.е. , то и – решение, ибо .

Между решениями однородной и неоднородной систем имеется простая связь.

Теорема 3. Решение однородной системы плюс решение неоднородной системы есть решение неоднородной системы.

Доказательство. Пусть х ⁰ и х ¹ таковы, что . Тогда . n

Теорема 4. Разность двух решений неоднородной системы есть решение однородной.

Доказательство.

. n

С помощью теорем 2–4 можно понять, как устроено множество решений неоднородной системы . Надо взять подпространство

решений однородной системы и «сдвинуть» его на произвольный вектор х ¹ – решение неоднородной системы, т.е. такой, что . Получим множество

,

состоящее из всех векторов вида , где – произвольное решение однородной системы. (Множество не зависит от того, какое «частное» решение х ¹ однородной системы мы возьмем.) Этот факт формулируют следующим образом: общее решение неоднородной системы есть частное решение неоднородной системы плюс общее решение однородной. Имеется ввиду, что если частное решение неоднородной х ¹ фиксировано, а х ⁰ «пробегает» все множество решений однородной системы, то сумма «пробегает» все множество решений неоднородной системы.

Сначала мы научимся находить общее решение однородной системы, а затем – общее решение неоднородной.

3. Метод Гаусса для получения общего решения однородной системы.

Рассмотрим однородную систему (2). Мы можем переставлять уравнения местами, прибавлять к одному уравнению другое, умноженное на число, и всякий раз получать новую систему, эквивалентную старой, то есть имеющую то же самое множество решений. Эти операции удобней производить над строками матрицы А системы, и ясно, что они соответствуют элементарным преобразованиям строк. Приведем с помощью элементарных преобразований матрицу А к ступенчатому виду. Переменные х_i, соответствующие угловым элементам (т.е. имеющие те же номера, что и номера столбцов, содержащих угловые элементы) назовем зависимыми, остальные – свободными.

Выпишем систему, отвечающую ступенчатому виду

и перенесем в каждом уравнении все члены со свободными переменными вправо. Слева останутся выражения, содержащие только зависимые переменные. Система приобретет вид:

зависимые свободные

Пусть для простоты х ₁, х ₂,..., х_r – зависимые, а х_{r+ 1},..., х_n – свободные. Тогда новая система имеет вид:

Итак, матрица коэффициентов при зависимых переменных – треугольная (квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю) и при этом . Это был прямой ход метода Гаусса.

Сделаем обратный ход: из последнего уравнения выразим х_r через свободные переменные и подставим полученное выражение в предпоследнее уравнение, затем выразим х_{r -1} через свободные переменные и подставим выражения для х_r, х_{r -1} в предыдущее («предпредпоследнее», т.е. (r - 2)-е) уравнение и т.д. В результате получим выражения зависимых переменных х ₁, х ₂,..., х_r через свободные х_{r+ 1},..., х_n

(3)

Выражения (3) дают хорошее описание всего множества решений однородной системы (2). В самом деле, свободным переменным х_{r+ 1},..., х_n мы можем придавать любые значения (они играют роль произвольных параметров для множества решений системы) в то время как зависимые переменные получают соответствующие значения, вычисляемые по формулам (3). Всякий раз мы получаем некоторое решение, и все решения могут быть таким образом получены. Поэтому систему (3) называют общим решением в координатной форме системы (2). Иногда его представляют так:

(4)

где отчетлива видно, что свободным переменным х_{r+ 1},..., х_n отводится роль параметров с ₁,..., с_{n - r}.

Отметим, что число параметров (n - r) плюс rank А = r равно n. Вспомните, что с подобной ситуацией мы уже встречались недавно в аналитической геометрии: прямую в пространстве, заданную как пересечение плоскостей, т.е. с помощью системы 2-х линейных уравнений с тремя неизвестными x, y, z, мы приводили к канонической, а затем параметрической форме. Прямая в пространстве R ³, проходящая через начало координат, есть одномерное подпространство, а параметрическая форма

– способ описания этого подпространства с помощью одного параметра t. Система (4) также есть способ параметрического описания (n - r)-мерного подпространства L – подпространства решений системы (2).

Общее решение (3) позволяет найти базис в подпространстве L решений системы (2) и представить общее решение как произвольную линейную комбинацию элементов этого базиса. Свободным переменным х_{r+ 1},..., х_n будем последовательно придавать значения, соответствующие координатам векторов стандартного базиса в R^{n - r}:

Не нашли, что искали? Воспользуйтесь поиском: