
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Уравнения множественной регрессии
Важным вопросом построения уравнения множественной регрессии является отбор наиболее существенных факторов из всего возможного множества факторов, вероятно, влияющих на отклик. Факторы, включаемые в уравнение, должны быть количественно измеримы. Если необходимо исследовать влияние качественного фактора, то ему необходимо придать количественную определенность.
При этом факторы могут находиться в той или иной степени зависимости друг от друга. Отрицательное влияние такой зависимости на уравнение регрессии описано выше, при обсуждении проблемы мультиколлинеарности факторов. Другим негативным явлением, возникающим при включении большого количества даже независимых факторов, является уменьшение значимости как всего уравнения в целом, так и его коэффициентов.
Наиболее приемлемым способом отбора факторов являются пошаговые процедуры. Среди таких процедур наиболее популярны:
· метод включения;· метод исключения.Заметим, что использование ни одной из процедур не гарантирует выбор такого набора факторов, который обеспечит нахождения наибольшего коэффициента детерминации.
Метод исключения решает проблему отбора фактором путем пошагового исключения наименее значимого фактора на основе сравнения модели полученной на данном шаге с моделью полученной на предыдущем шаге. Первоначально рассматривается полный набор факторов, процедура завершается тогда, когда исключение любого фактора из числа оставшихся приводит к существенному ухудшению построенной модели.
Метод включения решает проблему отбора фактором путем пошагового включения каждого фактора на основе сравнения качества модели полученной на данном шаге с моделью полученной на предыдущем шаге. Качество модели оценивается путем анализа величины скорректированного коэффициента множественной детерминации  .
.
На первом шаге строится уравнение регрессии, содержащее один наиболее информативный фактор. Выбор такого фактора можно сделать, например, путем сравнения коэффициентов парной корреляции между откликом и каждым из факторов. Фактор, у которого модуль коэффициента парной корреляции наибольший, является наиболее информативным. Далее можно построить уравнение парной регрессии и вычислить соответствующее значение скорректированного коэффициента детерминации 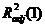 . Цифра в скобках показывает, что это значение вычислено при включении в модель одного фактора.
. Цифра в скобках показывает, что это значение вычислено при включении в модель одного фактора.
На втором шаге строим всевозможные двухфакторные модели, при этом одним из факторов будет фактор, включенный в модель на первом шаге. Среди этих двухфакторных моделей выбираем ту, у которой коэффициент детерминированности будет максимальным. Для этой модели вычислим скорректированный коэффициент детерминации  . Далее сравниваем этот коэффициент детерминации
. Далее сравниваем этот коэффициент детерминации  с коэффициентом детерминации
с коэффициентом детерминации 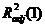 , полученным на предыдущем шаге. Если
, полученным на предыдущем шаге. Если  существенно больше
существенно больше 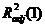 , то включение второго фактора в уравнение целесообразно, поскольку происходит увеличение объясненной доли вариации отклика. После этого можно переходить к третьему шагу. Если
, то включение второго фактора в уравнение целесообразно, поскольку происходит увеличение объясненной доли вариации отклика. После этого можно переходить к третьему шагу. Если  несущественно больше или меньше
несущественно больше или меньше 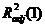 , то включение второго фактора в уравнение нецелесообразно и приходим к выводу, что целесообразно рассматривать уравнение, полученное на первом шаге.
, то включение второго фактора в уравнение нецелесообразно и приходим к выводу, что целесообразно рассматривать уравнение, полученное на первом шаге.
На третьем шаге строим всевозможные трехфакторные модели,, при этом первыми двумя из этих факторов будут факторы, включенные в модель на втором шаге. Далее действуем по следующему алгоритму:
· выбираем наилучшую среди этих трехфакторных моделей по величине коэффициента детерминированности;
· оцениваем предпочтительность использования трехфакторной модели по сравнению с двухфакторной, путем сравнения скорректированных коэффициентов детерминации  и
и  . В зависимости от результата увеличиваем количество факторов в модели до трех или ограничиваемся двумя факторами.
. В зависимости от результата увеличиваем количество факторов в модели до трех или ограничиваемся двумя факторами.
Описанный процесс продолжается до тех пор, пока включение очередного фактора обеспечивает улучшение модели.
Пример [7].
Исследовать зависимость между стоимостью грузовой автомобильной перевозки Y (тыс. руб), весом груза X1 (тонн) и расстоянием X2 (тыс. км) по 20 транспортным компаниям (табл.7.3).
Таблица 7.3.
| №п/п | Y | X1 | X2 |
| 1,1 | |||
| 2,55 | |||
| 7,5 | 1,7 | ||
| 2,4 | |||
| 1,55 | |||
| 11,5 | 0,6 | ||
| 2,3 | |||
| 15,8 | 1,4 | ||
| 2,1 | |||
| 1,3 | |||
| 0,35 | |||
| 5,8 | 1,65 | ||
| 13,8 | 3,5 | 2,9 | |
| 6,2 | 2,8 | 0,75 | |
| 7,9 | 0,6 | ||
| 5,4 | 3,4 | 0,9 | |
| 2,5 | |||
| 25,5 | 2,2 | ||
| 7,1 | 4,5 | 0,95 |
Требуется построить и оценить линейную модель множественной регрессии по следующему плану:
1. Вычислить описательные статистики для отклика и всех факторов.
2. Оценить визуально, построив соответствующие облака рассеяния величины Y в зависимости от X1 и X2, целесообразность использования линейного уравнения регрессии.
3. Вычислить и проанализировать:
· линейные коэффициенты парной и частной межфакторной корреляции;
· линейные коэффициенты парной и частной корреляции между каждым фактором и откликом.
4. Написать уравнение множественной регрессии  , оценить значимость его параметров, пояснить их экономический смысл. Коэффициенты уравнения вычислить четырьмя способами, используя:
, оценить значимость его параметров, пояснить их экономический смысл. Коэффициенты уравнения вычислить четырьмя способами, используя:
· систему нормальных уравнений (7.3);
· функцию ЛИНЕЙН();
· матричную формулу (7.28);
· надстройку «Анализ Данных» > «Регрессия».
5. Написать уравнение множественной регрессии в стандартизованном масштабе 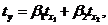 пояснить экономический смысл его параметров.
пояснить экономический смысл его параметров.
6. Вычислить средние частные коэффициенты эластичности 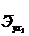 и
и  . Пояснить их экономический смысл.
. Пояснить их экономический смысл.
7. Вычислить множественный коэффициент корреляции 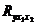 с использованием матрицы парных коэффициентов корреляции по формуле (7.11).
с использованием матрицы парных коэффициентов корреляции по формуле (7.11).
Полученный результат сравнить с результатом, полученным с помощью надстройки «Анализ Данных»> «Регрессия».
8. Вычислить коэффициентом множественной детерминации  двумя способами:
двумя способами:
· по определению, по формуле (7.8);
· с использованием матрицы парных коэффициентов корреляции по формуле (7.9).
Полученный результат сравнить с результатом, полученным с помощью надстройки «Анализ Данных»> «Регрессия».
Убедиться, что квадрат множественного коэффициента корреляции  совпадает с коэффициентом множественной детерминации
совпадает с коэффициентом множественной детерминации  , т.е. справедливо соотношение (7.10).
, т.е. справедливо соотношение (7.10).
Пользуясь шкалой Чеддока, дайте качественную оценку силы связи между откликом и факторами
9. С помощью F-критерия Фишера дать оценку надежности уравнения регрессии в целом и показателя тесноты связи 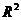 , используя результат, полученный с помощью надстройки «Анализ Данных»;
, используя результат, полученный с помощью надстройки «Анализ Данных»;
10. Вычислить исправленный (скорректированный, adjustable) коэффициент детерминации  с использованием соотношения (7.23) (здесь
с использованием соотношения (7.23) (здесь  ).
).
Полученный результат сравнить с результатом, полученным с помощью надстройки «Анализ Данных»> «Регрессия». Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.
11. Оценить значимость коэффициентов множественной регрессии с помощью t -критерия Стьюдента, используя результаты работы надстройки «Анализ Данных»> «Регрессия».
12. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора X1 после фактора X2 и фактора X2 после фактора X1.
13. Найти точечное прогнозное значение отклика при условии, что значение каждого фактора меньше максимального значения на 10% величины размаха исходных данных.
Пояснения по выполнению отдельных пунктов задания.
Решение проведем с использованием электронных таблиц MS Excel.
Исходные данные представлены на рис. 7.4а, и содержатся в интервале B3:D22, на рис.7.4.б приведены вычисленные средние значения, дисперсии и стандартные отклонения факторов и отклика.

Рис.7.4.а. Исходные данные задачи в MS Excel
К пункту 1.
1. Описательные статистики для отклика и всех факторов X1 и X2, могут быть вычислены с помощью с помощью надстройки MS Excel «Пакет Анализа – Описательные статистики».
К пункту 2.
Вытянутость облака точек на диаграмме рассеяния (рис. 7.5 а) вдоль наклонной прямой позволяет сделать предположение о том, что существует линейная связь между значениями переменных X1 - весом груза и Y- стоимостью грузовой автомобильной перевозки. Анализируя рис.7.5.б, можно заметить наличие прямой линейной связи между значениями переменных X2 - расстоянием и Y - стоимостью грузовой автомобильной перевозки.

Рис.7.4 б. Описательная статистика для исходных данных задачи с помощью с помощью надстройки MS Excel «Пакет Анализа – Описательные статистики».

Рис. 7.5 а. Облако рассеяния Y - X1

Рис. 7.5 б. Облако рассеяния Y - X2
К пункту 3.
Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.
Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент «Анализ данных» >Корреляция. Для этого:
1). В главном меню последовательно выберите пункты Сервис> Анализ данных> Корреляция. Щелкните по кнопке ОК;
2). Заполните диалоговое окно ввода данных и параметров вывода (рис. 7.6 а).

Рис. 7.6 а. Диалоговое окно ввода данных и параметров вывода для вычисления коэффициентов парной корреляции
Значения коэффициентов парной корреляции указывают на заметную связь стоимости перевозок Y как с весом груза – X1, так и расстоянием – X2 (ryx1 =0,66 и ryx2 =0,63). В то же время межфакторная связь rx1x2 =0,12 довольно слабая, т.е. явной мультиколлинеарности нет. В связи с вышеизложенным, можно сделать предварительный вывод, что нет оснований исключать факторы X1 или X2 из данной модели.
Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели.

Рис. 7.6 б. Результаты вычисления коэффициентов корреляции (интервал A54:D56) и коэффициентов частной корреляции.
Вычислим коэффициенты частной корреляции по рекуррентным формулам



Наиболее тесно связаны Y и X1 (ryx1 x2 =0,7513), связь Y и X2 чуть слабее: ryx2 x1= 0,7376, а межфакторная зависимость X1 и X2 не очень сильная |rx1x2 y| = 0,4987
Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за наличия между факторной зависимости они отличаются друг от друга:
ryx1= 0,6552; ryx1 x2= 0,7513; ryx2=0,6346; ryx2 x1=0, 7376.
Частные коэффициенты корреляции Y и X1, Y и X2 свидетельствуют о более сильных взаимосвязях независимых переменных, чем это показывают значения парных коэффициентов корреляции. Это произошло потому, что парный коэффициент корреляции завысил тесноту связи между X1 и X2 , занизив при этом тесноту связи между Y и X1, Y и X2
К пункту 4.
Вычисление параметров линейного уравнения множественной регрессии.
Система нормальных уравнений (7.3) в случае двух факторов будет иметь вид:

Вычисление коэффициентов этой системы и решение ее с помощью обратной матрицы приведено на рис. 7.7. Коэффициенты регрессии содержатся в интервале ячеек I96:I97. Таким образом, уравнение регрессии примет вид:


Рис. 7.7. Вычисление параметров линейного уравнения множественной регрессии с помощью системы нормальных уравнений.
Нахождение коэффициентов регрессии можно выполнить, используя функцию ЛИНЕЙН() (рис. 7.8).

Рис. 7.8. Результаты применения функции ЛИНЕЙН().
Нахождение коэффициентов регрессии матричным методом показано на рис. 7.9. Коэффициенты регрессии содержатся в интервале ячеек I127:I129.

Рис. 7.9. Вычисление параметров линейного уравнения множественной регрессии с помощью матричного метода.
Операцию нахождения коэффициентов регрессии можно провести с помощью инструмента «Анализ Данных» «Регрессия». Следует помнить, что в отличие от парной регрессии в диалоговом окне при заполнении параметра «входной интервал Х» следует указать не один столбец, а все столбцы, содержащие значения факторных признаков (см.рис. 7.10.а). Результат приведен на рис. 7.10.б
По результатам всех вычислений уравнение множественной регрессии имеет вида 
Величины b1 и b2 указывают, что с увеличением значений X1 и X2 на единицу отклик увеличивается соответственно на 1,16 и на 15,10 тыс.руб.

Рис. 7.10 а. Диалоговое окно инструмента «Анализ Данных» «Регрессия».

Рис. 7.10 б. Результаты применения инструмента «Анализ Данных» «Регрессия».
К пункту 5.
Для вычисления коэффициентов уравнения регрессии в стандартизованном масштабе используем формулы (7.6).

С учетом этого, уравнение регрессии в стандартном масштабе будет иметь вид:

То есть, с ростом груза на одну сигму при неизменном расстоянии стоимость грузовых автомобильных перевозок увеличивается в среднем на 0,58 сигмы. Поскольку значения коэффициентов отличаются друг от друга незначительно, то влияние на стоимость грузовых автомобильных обоих факторов приблизительно одинаково.
К пункту 6.
Рассчитаем средние коэффициенты эластичности


С увеличением среднего веса груза на 1% от его среднего уровня средняя стоимость перевозок возрастет на 0,71% от своего среднего уровня; при увеличении среднего расстояния перевозок на 1% - средняя стоимость доставки груза увеличится на 1,05%. Различия в силе влияния факторов на результат, полученные при сравнении уравнения регрессии в стандартизованном масштабе и коэффициентов эластичности, объясняются тем, что при вычислении коэффициентов эластичности учитывают поведение уравнения регрессии в окрестности средних значений.
К пункту 7
Вычислить множественный коэффициент корреляции  с использованием матрицы парных коэффициентов корреляции по формуле (7.11).
с использованием матрицы парных коэффициентов корреляции по формуле (7.11).
Все промежуточные вычисления и результаты расчетов в MS Excel приведены на рис.7.11. Получено значение  =0.86, следовательно, связь между результирующим показателем Y и набором объясняющих переменных факторов X1 и X2 тесная.
=0.86, следовательно, связь между результирующим показателем Y и набором объясняющих переменных факторов X1 и X2 тесная.
Вычисление индекса корреляции с использованием формулы  приведено в ячейке С179 на том же рис.7.11
приведено в ячейке С179 на том же рис.7.11
Полученный результат совпадает с результатом, полученным с помощью надстройки «Анализ Данных» > «Регрессия», содержащимся в ячейке В136 («Множественный R») на рис.7.10.б.

Рис. 7.11 а. Вычисление индекса корреляции в MS Excel в режиме отображения данных.

Рис. 7.11 б. Вычисление индекса корреляции в MS Excel в режиме отображения формул.
К пункту 8.
Величина коэффициента множественной детерминации  , рассчитанная по определению (по формуле (7.8) и с использованием коэффициентов уравнения множественной регрессии в стандартизованном масштабе (по формуле (7.9) оказалась одинаковой и равной 0.74. Расчеты приведены на рис.7.12
, рассчитанная по определению (по формуле (7.8) и с использованием коэффициентов уравнения множественной регрессии в стандартизованном масштабе (по формуле (7.9) оказалась одинаковой и равной 0.74. Расчеты приведены на рис.7.12

Рис. 7.12 а. Вычисление коэффициента множественной детерминации в MS Excel в режиме отображения данных.

Рис. 7.12 б. Вычисление коэффициента множественной детерминации в MS Excel в режиме отображения формул.
Полученный результат совпадает с результатом, полученным с помощью надстройки «Анализ Данных» > «Регрессия», содержащимся в ячейке В136 («Множественный R») на рис.7.10.б.
Поскольку коэффициент множественной детерминации оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата и  , то эта доля составляет 74 % и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом. О шкале Чеддока сила связи оценивается как высокая.
, то эта доля составляет 74 % и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом. О шкале Чеддока сила связи оценивается как высокая.
К пункту 9.
Оценку надежности уравнения регрессии в целом и показателя тесноты связи 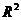 дает F - критерий Фишера.
дает F - критерий Фишера.
По данным дисперсионного анализа, представленным в интервале ячеек A142:F146 на рис.7.10.б, Fнабл =24,17. Вероятность случайно получить такое значение F – критерия составляет 1,07*10-5 , ячейка F144 («Значимость F»), что не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи 
Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены в разделе регрессионная статистика.
К пункту 10.
Вычислить исправленный (скорректированный, adjustable) коэффициент детерминации  с использованием соотношения
с использованием соотношения  , где р - количество факторов (здесь р =2). Получаем
, где р - количество факторов (здесь р =2). Получаем  =0,7092. Такое же значение получено в ячейке В138 («Нормированный R-квадрат») на рис.7.10.б.
=0,7092. Такое же значение получено в ячейке В138 («Нормированный R-квадрат») на рис.7.10.б.
Заметим, что  <
<  , что соответствует теории.
, что соответствует теории.
К пункту 11.
Значения случайных ошибок параметров a, b1 и b2 с учетом округления:
ma=6,4471; mb1=0,2463; mb2=3,3530.
Эти значения используются для расчета t - критерия Стьюдента по формуле 7.20:

Модули вычисленных величин следует сравнить с tкрит. Для практических расчетов достаточно помнить, чтоесли значение t -критерия > 2-3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются a, b1 и b2.
Процедура проверки значимости коэффициентов уравнения с помощью инструмента «Анализ Данных» «Регрессия» существенно проще, поскольку все промежуточные операции выполняются автоматически. На рис. 7.10.б. в интервале B149:Е151 приведены значения коэффициентов регрессии, стандартных ошибок, t – статистики (t-наблюдаемые) и Р – значения соответственно. Для анализа значимости коэффициентов регрессии столбец «P-значение» в интервале Е86:Е88: если онменьше принятого нами уровня значимости (в настоящей работе уровень значимости принят равным 0,05), делают вывод о неслучайной природе данного значения коэффициента, т.е. о том, что он статистически значим и надежен. В противоположном случае принимается гипотеза о случайной природе значения этого коэффициента уравнения. Здесь все P<0,05, что позволяет подтвердить сделанный ранее вывод о статистической значимости всех параметров регрессии.
К пункту 12.
Для оценки целесообразности включения в модель фактора xi после фактора х2 и фактора х2 после фактора х1 вычислим значения частных F-критериев Фишера

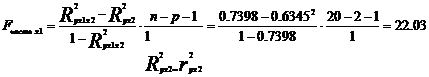
Частный F -критерий –  показывает статистическую зависимость включения фактора x2 в модель после того, как в нее включен фактор x1.
показывает статистическую зависимость включения фактора x2 в модель после того, как в нее включен фактор x1.
 = 20,29. Найдем Fкрит =4,45 при принятом уровне значимости a =0,05 (5%) (число степеней свободы числителя и знаменателя равны 1 и 17 соответственно).
= 20,29. Найдем Fкрит =4,45 при принятом уровне значимости a =0,05 (5%) (число степеней свободы числителя и знаменателя равны 1 и 17 соответственно).  = 20,29 > Fкрит =4,45. Следовательно, включение в модель фактора x 2 – расстояния, после того, как уравнение включен фактор x1 – вес груза, статистически целесообразно: прирост факторной дисперсии за счет дополнительного признака x2 оказывается значительным, существенным; фактор x2 следует включать в уравнение после фактора x1.
= 20,29 > Fкрит =4,45. Следовательно, включение в модель фактора x 2 – расстояния, после того, как уравнение включен фактор x1 – вес груза, статистически целесообразно: прирост факторной дисперсии за счет дополнительного признака x2 оказывается значительным, существенным; фактор x2 следует включать в уравнение после фактора x1.
Поменяем первоначальный порядок включения факторов в модель и рассмотрим вариант включения x1 после x 2. Для этого вычислим Fчасти x1, оно равно 22,03.
При том же уровне значимости a =0,05 (5%). Fкрит =4,45 и.  > Fкрит. Следовательно, значение частного F -критерия для дополнительно включенного фактора x1 не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора x1 является существенным. Фактор x1 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора x 2.
> Fкрит. Следовательно, значение частного F -критерия для дополнительно включенного фактора x1 не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора x1 является существенным. Фактор x1 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора x 2.
К пункту 13.
Вычислим значение каждого фактора с учетом того, что максимальные значения и размахов уже были вычислены и приведены на рис.7.4.б. 
Полученные результаты вычислений подставим в уравнение множественной регрессии

Общий вывод состоит в том, что множественная линейная модель

с факторами Х1 и Х2 имеет коэффициент детерминированности  =0,73. Она содержит информативные факторы X 1 и X2. Уравнение парной регрессии является простым, хорошо детерминированным, пригодным для анализа и для прогноза
=0,73. Она содержит информативные факторы X 1 и X2. Уравнение парной регрессии является простым, хорошо детерминированным, пригодным для анализа и для прогноза

Рис. 7.13 а. Вычисление точечного значения прогноза в MS Excel в режиме отображения данных.

Рис. 7.13 б. Вычисление точечного значения прогноза в MS Excel в режиме отображения формул.
.
Задание
Для ряда регионов представлена информация об объёмах Y (у.е.) продаж фирмы «Галактика»и ее затратах на рекламу в этих регионах – X1, а также индекс потребительских доходов в этих регионах – X2. Построить и оценить линейную модель множественной регрессии по плану, приведенному в примере, изложенном выше.
Исходные данные взять из файла «Econometric_LabRab_7.xls».
Не нашли, что искали? Воспользуйтесь поиском: