Компактні топологічні простори. Нехай X – топологічний простір

Нехай X – топологічний простір. Деяка сукупність підмножин називається покриттям простору X, якщо .

Якщо , то система підмножин називається покриттям множини А, якщо .

Якщо всі - відкриті, то покриття називається відкритим. Підпокриттям називається деяка сукупність множин з покриття. Топологічний простір X називається компактним, якщо з будь-якого відкритого його покриття можна виділити скінченне підпокриття.

Приклади:

1. Числова пряма не є компактним простором, оскільки з його покриття інтервали вигляду неможливо виділити скінченне підпокриття.
2. Скінченний відкритий інтервал (0, 2) не є компактним простором, оскільки з його покриття інтервали вигляду неможливо виділити скінченне підпокриття.
3. Замкнений інтервал є компактним простором, що доводиться в лемі Гейне-Бореля.

Нехай Х – деяка множина, - деяка система підмножин з множини Х. називається центрованою, коли кожна скінченна підсистема підмножин з має непустий перетин.

Твердження 1 (критерій компактності простору):

Топологічний простір Х є компактним тоді і тільки тоді, коли кожна центрована система його замкнених підмножин має непустий перетин.

Доведення: Припустимо, що простір Х – компактний і в ньому існує центрована система замкнених підмножин , яка має пустий перетин, тобто , тоді простір . Оскільки - замкнені, то 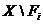- відкриті, а з рівності випливає, що підмножини утворюють відкрите покриття простору Х.

Оскільки простір – компактний, то це покриття містить скінченне підпокриття, тобто існують підмножини , а це протирічить тому, що система є центрованою.

Припустимо,що простір Х задовольняє умову критерію і покажемо, що Х є компактним. Нехай 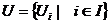- деяке відкрите покриття простору Х, тобто , тоді . Оскільки - відкриті, то - замкнені. А оскільки , то згідно умові критерію не може бути центрованою. Тоді існує скінченна сукупність підмножин , тобто підмножини утворюють скінченне відкрите підпокриття простору Х. Х є компактним. Що і треба було довести.

Підмножина А топологічного простору Х називається компактною, якщо підпростір є компактним.

Твердження 2: Підмножина А топологічного простору Х є компактною тоді і тільки тоді, коли з кожного покриття множини А відкритими в Х підмножинами можна виділити скінченне підпокриття.

Доведення: Припустимо, що підмножина А є компактною. Нехай - деяке покриття множини А відкритими в просторі Х підмножинами, тобто 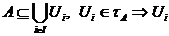- відкриті. Тоді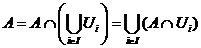

За означенням :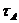

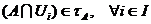
Таким чином, підмножина утворює відкрите покриття підпростору .

Оскільки множина А – компактна, то і - компактний, і значить з його відкритого покриття можна виділити скінченне підпокриття: утворюють скінченне підпокриття множини А відкритими у просторі Х підмножинами, тобто А задовольняє умовам твердження.

Навпаки: припустимо тепер, що А задовольняє умову твердження, тобто покажемо, що А – компактна.

Нехай - довільне покриття відкритими підмножинами простору , тобто . За означенням

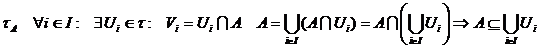
Таким чином, утворюють покриття множини А відкритими в Х підмножинами. За умовою твердження з цього покриття можна виділити скінченне підпокриття, тобто утворюють скінченне відкрите підпокриття підпростору . - компактний, а А – компактна в Х. Все доведено.

Твердження 3: Всяка замкнена підмножина А топологічного простору Х є компактною множиною цього простору.

Доведення: За означенням компактної множини, нам треба довести, що підпростір є компактним. Нехай 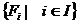- деяка центрована система замкнених в просторі підмножин. За властивістю замкнених підмножин підпростору .

А оскільки підмножина А також замкнена в усьому просторі Х, то показує, що підмножини - замкнені в просторі Х. 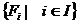є і центрованою системою підмножин замкнених в просторі Х. Оскільки Х є компактним, ця система має непустий перетин. Отже, ми довели, що довільна центрована система 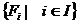замкнених підмножин підпростору має непустий перетин. За твердженням 1 цей підпростір є компактним. І все доведено.

Не нашли, что искали? Воспользуйтесь поиском: