Оценка приближения.

Из неравенств (6) имеем

Просуммировав геометрическую прогрессию, получим

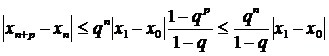
Устремляя p→∞, окончательно находим

(10)

Таким образом, сходимость процесса итерации тем быстрее, чем меньше число q.

Для оценки погрешности можно дать и другую полезную формулу. Пусть g (x)= x - φ (x), . Учитывая, что g(ξ)=0, получим

, следовательно,

(11)

т.е.

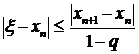(12)

Используя неравенство (5) имеем также

(13)

Отсюда, в частности, следует, что если q ≤0.5, то , т.е. в этом случае из неравенства вытекает неравенство .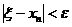

Формула (13) дает возможность оценить погрешность приближенного значения x_n по расхождению двух последовательных приближений x_n и x_{n- 1}. Из формулы (13) следует, что процесс итерации следует продолжать до тех пор, пока не будет выполнено неравенство

,

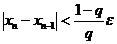где ε – заданная абсолютная погрешность корня ξ и . Тогда 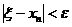и ξ=x_n± ε.

Заметим, что учитывая (3) и равенство ξ= φ(ξ), можно записать

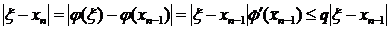, т.е. . Таким образом, при сходящемся итерационном процессе погрешность 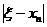стремится к нулю монотонно, т.е. каждое последующее приближение x_n является более точным, чем предшествующее x_{n- 1}.

Замечание. Если при применении метода простой итерации два последовательных приближения x_{n- 1} и x_n совпадают между собой с заданной точностью ε (например, для этих приближений установились m первых значащих цифр), то в общем случае из этого не следует, что с той же точностью справедливо равенство ξ= x_n (т.е. что в приведенном примере m знаков приближенного числа x_n являются верными). Легко показать (это следует из (13)), что если близка к единице, то величина 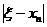может оказаться большой и при малых величинах .

Не нашли, что искали? Воспользуйтесь поиском: