Формулы Ньютона-Котеса.

Формулы для приближенного вычисления интегралов , которые получаются заменой подынтегральной функции интерполяционным полиномом Лагранжа с равноотстоящими узлами, называются формулами Ньютона-Котеса.

Пусть , , . Заменяя функцию f (x) интерполяционным полиномом Лагранжа, получим приближенную квадратурную формулу:

, (1)

где A_i – некоторые постоянные коэффициенты. Получим для них явные выражения. Для этого запишем полином Лагранжа в виде: ,

где . Введя обозначения и , получим

.

Отсюда . Так как , сделав замену переменной в определенном интеграле, получим

Используя выражение , записывают , где

, i =0,1,2,…, n (2)

– постоянные, называемые коэффициентами Котеса. Квадратурная формула (1) при этом приобретает вид:

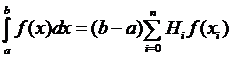. (3)

Коэффициенты Котеса H_i не зависят ни от подынтегральной функции, ни от промежутка интегрирования и могут быть вычислены раз навсегда. Нетрудно убедиться, что справедливы соотношения

1) , 2) H_i = H_n-i.

Частными случаями формул Ньютона-Котеса являются формула трапеций (при n =1) и формула Симпсона (n =2).

Формула трапеций

Применяя формулы (2) при n =1, получаем

, , тогда

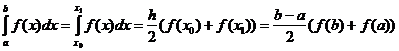(4)

Формула (4) является формулой трапеций для вычисления определенного интеграла. Геометрический смысл формулы трапеций заключается в том, что кривая, являющаяся графиком подынтегральной функции, заменяется отрезком прямой (n =1 – интерполяционный полином является линейной функцией), проходящей через точки с координатами (a, f (a)) и (b, f (b)), за приближенное значение искомой площади криволинейной трапеции принимается площадь полученной трапеции. Погрешность вычислений при этом часто оказывается достаточно большой. Для повышения точности отрезок интегрирования [ a, b ] разбивают на m равных частей и, пользуясь свойством определенного интеграла

,

применяют формулу трапеций на каждом из полученных отрезков [ x_i, x_{i +1}]. В результате получается обобщенная формула трапеций:

, (5)

где m – число разбиений отрезка интегрирования. Геометрически это означает, что криволинейная трапеция разбивается на m трапеций, а кривая y = f (x) заменяется ломаной.

Формула Симпсона

Применяя формулы (2) при n =2, получаем H ₀=1/6, H ₁=2/3, H ₂=1/6 и

(6)

Аналогично обобщенной формуле трапеций получают обобщенную формулу Симпсона

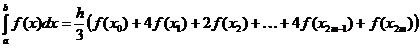. (7)

В формуле Симпсона число разбиений отрезка интегрирования является четным.

Геометрический смысл формулы Симпсона заключается в том, что график подынтегральной функции заменяется параболой (n =2, график полинома второй степени - парабола), проведенной через точки с координатами (a, f (a)), ((a + b) / 2, f ((a + b) / 2)), (b, f (b)), а затем вычисляется площадь криволинейной трапеции, ограниченной этой параболой. Для обобщенной формулы Симпсона график подынтегральной функции заменяется набором парабол, проведенных через каждые три соседние точки на графике данной функции, получающиеся при разбиении отрезка интегрирования.

Не нашли, что искали? Воспользуйтесь поиском: