Уравнения движения заряда в поле

Заряд, находящийся в поле, не только подвергается воздействию со стороны поля, но и в свою очередь сам влияет на поле, изменяя его. Однако, если заряд не велик, то его действием на поле можно пренебречь. В этом случае можно считать, что само поле не зависит ни от координат, ни от скорости заряда. Условия, при котором заряд считается малым, мы рассматривать не будем.

Уравнения движения заряда во внешнем поле получаются варьированием действия, т.е. даются уравнениями Лагранжа.

(3.12)

где определяется формулой (3.4)

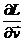есть обобщенный импульс (см (3.5))

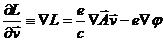
По известной формуле векторного анализа

,

где любые два вектора. В нашем случае дифференцирование по производится при постоянной 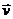. Поэтому

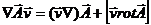
отсюда

Уравнение Лагранжа имеет вид

есть полная производная от по времени; она складывается из двух частей: из скорости изложения векторного потенциала со временем в данной точке и скорости изменения при переходе от одной точки пространства к другой

Учитывая это, получаем

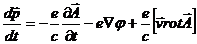(3.13)

Это и есть уравнение движения частицы в электромагнитном поле. Слева стоит производная от импульса по времени. Следовательно, выражение в правой части (3.13) есть сила, действующая на заряд в электромагнитном поле. Мы видим, что эта сила состоит из двух частей: первая часть (первый и второй члены) не зависят от скорости частицы. Вторая часть (третий член) зависит от скорости частицы, а именно пропорционально величине скорости и перпендикулярна к ней.

Силу первого рода, отнесенную к заряду, равному единице, называют напряженностью электрического поля . Итак,

(3.14)

Множитель при скорости, точнее при , в силе второго рода, называют напряженностью магнитного поля; обозначим ее через

(3.15)

Если , а 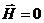- поле электрическое, если , а - поле магнитное.

Электромагнитное поле является наложением электрического и магнитного. (3.13) можно теперь переписать в виде

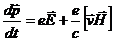(3.16)

Стоящее справа выражение называется Лоренцовой силой. Первая ее часть – сила, с которой действует на заряд электрическое поле, направлена по полю; вторая часть – сила, с которой действует на заряд магнитное поле, направленная перпендикулярно скорости движения заряда и направлению магнитного поля .

Для скоростей импульс 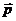переходит в свое классическое выражение 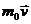. Тогда имеем

(3.17)

Выведем еще уравнение, определяющее изменение кинетической энергии частицы со временем, т.е. энергии

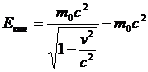
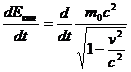
Легко убедиться, что , откуда

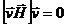подставляя из (3.16) и замечая, что , имеем

(3.18)

Изменение кинетической энергии со временем есть работа произведенная полем над частицей (в единицу времени). Из (3.18) видно, что эта работа производится только электрической составляющей поля. Сила, с которой магнитное поле действует на частицу, всегда перпендикулярна скорости. Это обстоятельство обуславливает то, что магнитное поле не производит работы над движущимися в нем зарядом.

Уравнение механики инвариантны относительно перемены знака у времени; это значит, что время изотропно и если возможно какое-то движение, при котором система проходит те же состояния в обратном порядке.

Легко видеть, что то же самое имеет место и в электромагнитном поле. Однако при этом вместе с заменой знака на 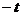надо изменить знак магнитного поля. В самом деле, (3.16) не меняется, если произвести замену

(3.19)

При этом согласно (3.14) и (3.15), скалярный потенциал не меняется, а векторный меняет знак:

(3.20)

Таким образом, если в электромагнитном поле возможно некоторое движение, то возможно и обратное движение в поле с обратным направлением .

§ 3 Градиентная инвариантность

Всякое поле характеризуется тем действием, которое оно оказывает на движение находящихся в нем зарядов. Из уравнения движения (3.16) видно, что это действие определяется величинами напряженности и . Поэтому два поля физически тождественны, если они характеризуются одними и теми же векторами и . Потенциалы 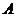и 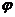, как видно из (3.14) и (3.15), вполне однозначно определяют и , т.е. поле. Однако одному и тому же полю могут соответствовать различные потенциалы. Чтобы убедиться в этом, прибавим к каждой компоненте 4-потенциала 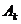величину , где 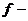произвольная функция от координат и времени. Тогда потенциал 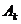переходит в

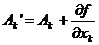(3.21)

При такой замене в интервале действия (3.1) появится дополнительный член, представляющий собой полный дифференциал

что не влияет на уравнения движения.

Если вместо 4-потенциала ввести скалярный и векторный и вместо координат 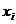- координаты 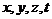, то четыре равенства (3.21) можно написать в виде

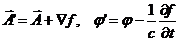(3.22)

В связи с тоем, что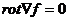

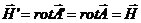
кроме того

Итак, преобразование (3.21) не изменяет поля. Потенциал определены поэтому не однозначно-векторный потенциал определен с точностью до градиента произвольной функции, а скалярный с точностью до производной по времени от той же функции.

Физический смысл имеют лишь те величины, которые инвариантны по отношению к преобразованию (3.22) потенциалов; в частности, все уравнения должны быть инвариантны по отношению к этому преобразованию. Эту инвариантность называют градиентной (калибровочной).

Описанная неоднозначность потенциалов дает возможность выбрать их так, чтобы они удовлетворяли одному произвольному, дополнительному условию, - одному, т.к. мы можем произвольно выбрать одну функцию в (2.22). В частности всегда можно выбрать потенциалы поля так, чтобы скалярный потенциал и был равен нулю, или один из компонентов векторного потенциала обращался в нуль.

Не нашли, что искали? Воспользуйтесь поиском: