Электростатическое поле. Закон Кулона.

Мы сформулировали в предыдущей главе общие уравнения электромагнитного поля и основные теоремы электродинамики. Теперь можно перейти к обсуждению различных частных случаев электромагнитных полей. При этом будем последовательно переходить от простейших к более сложным случаям.

Самым простым примером электромагнитного поля является поле неподвижных зарядов. Выпишем уравнения Максвелла для этого случая

(4.1)     (4.2)

Система уравнений электромагнитного поля в этом случае распадается на систему независимых уравнений для электрического и магнитного полей. Решение системы уравнений для магнитного поля, не зависящего от времени, имеет тривиальный вид

Это означает, что неподвижные заряды не окружены магнитным полем. Электрическое поле, как это следует из (4.1), полностью определяется неподвижно распределенной в пространстве системой зарядов. Вид второго из уравнений (4.1) показывает, что вектор может быть представлен как градиент скалярной функции. Учитывая, помимо того, соотношение (3.14) и то обстоятельство, что входящий в выражение (3.14) векторный потенциал не зависит от времени (заметим, что ), вектор можно записать

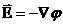
(4.3)

Подставляя (4.3) во второе из уравнений (4.1), получим

(4.4)

Это уравнение называется уравнением Пуассона. При заданном распределении зарядов в пространстве оно определяет потенциал 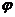постоянного электрического поля. В пустоте, когда , имеем

(4.5)

(4.5) называется уравнением Лапласа. Оператор фигурирующий в (4.4) и (4.5) имеет вид

(4.6)

Уравнение (4.5) наводит на мысль, что функция 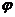не имеет ни максимума, ни минимума. В самом деле, если 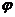имеет экстремум, то это означает, что и 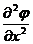, имеют одинаковый знак. Но последнее означает, что , что противоречит уравнению (4.6).

Определим поле, создаваемое конечным зарядом. Из соображений симметрии следует, что это поле будет радиальным, то есть будет направлено по радиусу – вектору, проведенному из точки, в которой находится заряд е, в точку наблюдения. Ясно также, что абсолютная величина Е поля будет зависеть от расстояния R до заряда. Для нахождения этой абсолютной величины применим уравнение в интегральной форме . Поток электрического поля через шаровую поверхность с радиусом R, проведенную вокруг заряда е, равен , это поток должен быть равен е. Отсюда находим:

.

В векторном виде

(4.7)

Итак, поле создаваемое точечным зарядом, обратно пропорционально квадрату расстояния от этого заряда. Это – так называемый закон Кулона. Потенциал этого поля есть, очевидно,

(4.8)

В случае системы точечных зарядов в силу принципа суперпозиции имеем

(4.9)

где расстояние от заряда до точки наблюдения. Если ввести плотность заряда , то эта формула имеет вид

(4.10)

где - расстояние от элемента объема до точки наблюдения.

Отметим здесь математическое соотношение получающееся при подстановке в (4.4) значения для точечного заряда, т.е. . Мы находим тогда

(4.11)

Не нашли, что искали? Воспользуйтесь поиском: