
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Электростатика анизотропного диэлектрика.
В анизотропной диэлектрической среде(монокристалл) линейная связь между  и
и  имеет более сложный вид, не сводящийся к простой пропорциональности. Наиболее общий вид такой зависимости дается выражением
имеет более сложный вид, не сводящийся к простой пропорциональности. Наиболее общий вид такой зависимости дается выражением

| (3.65) |
где  - постоянный вектор изначальной диэлектрической индукции. Он может быть отличным от нуля для некоторых кристаллов, которые в условиях термодинамического равновесия, прибывают в состоянии самополяризации.
- постоянный вектор изначальной диэлектрической индукции. Он может быть отличным от нуля для некоторых кристаллов, которые в условиях термодинамического равновесия, прибывают в состоянии самополяризации.  оказываются малыми по сравнению с внутри молекулярными полями. Однако большинство кристаллов не допускает существование постоянного вектора
оказываются малыми по сравнению с внутри молекулярными полями. Однако большинство кристаллов не допускает существование постоянного вектора  в силу кристаллографической симметрии, так что
в силу кристаллографической симметрии, так что

| (3.66) |
В соответствии с (3.23)независимо от вида материального уравнения мы имеем

| (3.67) |
Отсюда, в частности, следовало (см.(3.25))
 .
.  т.е.
т.е. 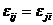
 . Проинтегрируем (3.67), учитывая (3.65). Тогда имеем (см. аналогичные формулы (3.21), (3.34))
. Проинтегрируем (3.67), учитывая (3.65). Тогда имеем (см. аналогичные формулы (3.21), (3.34))

| (3.68) |
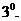 Тензор
Тензор  - симметричный, вещественный вектор второго ранга. Его можно провести к главным осям (к диагональному виду), так что
- симметричный, вещественный вектор второго ранга. Его можно провести к главным осям (к диагональному виду), так что

| (3.69) |
Все кристаллы можно разбить на три множества:
1) С низкой симметрией 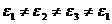 (двухосные кристаллы). Часть из трех главных осей могут совпасть с некоторыми из кристаллографических направлений (или даже все три).
(двухосные кристаллы). Часть из трех главных осей могут совпасть с некоторыми из кристаллографических направлений (или даже все три).
2) 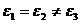 (одноосные кристаллы). Одна из главных осей совпадает при этом с кристаллографической осью симметрии.
(одноосные кристаллы). Одна из главных осей совпадает при этом с кристаллографической осью симметрии.
3)  . Направление главных осей произвольны. Это изотропный кристалл. Кристаллы кубической симметрии в отношении диэлектрических свойств не отличаются от изотропных тел.
. Направление главных осей произвольны. Это изотропный кристалл. Кристаллы кубической симметрии в отношении диэлектрических свойств не отличаются от изотропных тел.
Наконец, заметим, что если  , то в этом случае тело носит название пироэлектрика (Пироэлектрик – диэлектрик с отличной от нуля спонтанной поляризацией в отсутствии внешнего поля).
, то в этом случае тело носит название пироэлектрика (Пироэлектрик – диэлектрик с отличной от нуля спонтанной поляризацией в отсутствии внешнего поля).
§19 Пьезоэлектрики.
Внутренние напряжения, появляющиеся в изотропном диэлектрике в электрическом поле, представляет собой эффект, квадратичный по полю(см формулу(3..107) и (3.108.)). Изотропный диэлектрик не может быть пироэлектриком, т.е. в этом случае (3.65) не имеет место, а имеет место слагаемое. Аналогичный эффект имеет место и в ряде анизотропных кристаллов. Однако при определенных типах симметрии внутренние напряжения, возникающие в электрическом поле, в кристаллах пропорциональных первой степени поля (пьезоэлектрики). Соответственно имеет место и обратный эффект - деформирование диэлектрики сопровождается появление в нем поля, пропорционального первой степени деформации.
Если учитывать лишь основной, линейный эффект, то, пренебрегая в общей формуле (3.109) квадратичным по полю членом*, имеем
 (3.111)
(3.111)
В этой формуле  - свободная энергия, приходящая на единицу объема деформированного кристалла. Будем далее пользоваться термодинамическими величинами, отнесенными к количеству вещества, заключенного в единице объема недеформированного тела. Обозначим пока соответствующую плотность свободной энергии
- свободная энергия, приходящая на единицу объема деформированного кристалла. Будем далее пользоваться термодинамическими величинами, отнесенными к количеству вещества, заключенного в единице объема недеформированного тела. Обозначим пока соответствующую плотность свободной энергии  . Очевидно,
. Очевидно,  ,
,  , где
, где  свободная энергия объема
свободная энергия объема  до деформации, после деформации это количество свободной энергии стало приходиться на объем
до деформации, после деформации это количество свободной энергии стало приходиться на объем  . Т.о.,
. Т.о.,
 .
.
Учитывая, что  (
( - координаты частицы до деформации,
- координаты частицы до деформации,  - после деформации,
- после деформации,  - смещение в процессе деформации), имеем
- смещение в процессе деформации), имеем
 , где
, где  ,
, 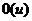 - содержит квадратичные по
- содержит квадратичные по  и высшие члены. Т.к.
и высшие члены. Т.к.  , то
, то 
Имеем далее
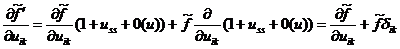
Здесь учтено, что  квадратично по
квадратично по  .
.
Опуская далее у  индекс «′» и понимая под
индекс «′» и понимая под  - свободную энергию, приходящую на количество вещества в единице объема недеформированного тела имеем
- свободную энергию, приходящую на количество вещества в единице объема недеформированного тела имеем
 (3.112)
(3.112)
Соответственно для  имеем
имеем
 (3.113)
(3.113)
Здесь первые два слагаемых относится к единице объема недеформированного кристалла; третье слагаемое перенесено из формулы (3.23) и поэтому, строго говоря, оно относится к единице объема деформированного тела. Поэтому вместо третьего слагаемого надо было бы писать
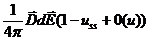
Отбрасывая члены типа  , мы допускаем ошибку, которая в случае пьезоэлектрика является величиной более высокого порядка малости, чем остальные члены в (3.113)
, мы допускаем ошибку, которая в случае пьезоэлектрика является величиной более высокого порядка малости, чем остальные члены в (3.113)
В (3.113) независимыми переменными являются  . Иногда в качестве таковых удобнее пользоваться
. Иногда в качестве таковых удобнее пользоваться  . Для этого надо ввести термодинамический потенциал
. Для этого надо ввести термодинамический потенциал
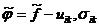 (3.114)
(3.114)
Для дифференциала этой величины
 (3.115)
(3.115)
Заметим, что введение  по формулам (3.114)-(3.115) связано со справедливостью соотношения (3.112) и потому имеет место только для пьезоэлектриков.
по формулам (3.114)-(3.115) связано со справедливостью соотношения (3.112) и потому имеет место только для пьезоэлектриков.
Перейдем теперь к описанию пьезоэлектрических свойств кристаллов. Выбрав величины  и
и  в качестве независимых переменных, мы должны рассмотреть индукцию
в качестве независимых переменных, мы должны рассмотреть индукцию  как их функцию, а в разложении этой функции надо сохранить члены первого порядка по ним. В наиболее общем виде это линейное разложение для пьезоэлектрика записывается
как их функцию, а в разложении этой функции надо сохранить члены первого порядка по ним. В наиболее общем виде это линейное разложение для пьезоэлектрика записывается
 (3.116)
(3.116)
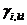 составляет тензор 3-го.Поскольку
составляет тензор 3-го.Поскольку
 , то
, то
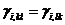
здесь мы обделили запятой симметричную пару индексов  от третьего индекса.
от третьего индекса.
Соответствующие дополнительные члены появятся и в термодинамических величинах. Т.к для диэлектрика при отсутствии поля
 ,
,
То соответствие с этим законом для пьезоэлектрического кристалла в отсутствии поля
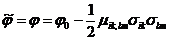
Так как согласно(3.115)
 ,
,
С одной стороны, и имеем место (3.116),- с другой, то для пьезоэлектрика в поле
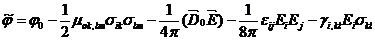
Исходя из (3.118) и (3.115), имеем
 (3.119)
(3.119)
Подчеркиваем, что  относиться к диэлектрику в отсутствии поля.(3.119) есть по сути дела закон Гука для пьезоэлектрика.
относиться к диэлектрику в отсутствии поля.(3.119) есть по сути дела закон Гука для пьезоэлектрика.
Определение поля в пьезоэлектрике должно производиться одновременно с определением его деформации и представляет собой совместную задачу электростатики и теории упругости. Именно следует искать совместное решение уравнений электростатики.
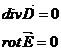
С  из (3.116) и уравнений упругости равновесия
из (3.116) и уравнений упругости равновесия
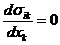
С соответствующими границами условиями на поверхности тела и с учетом связи между  и деформации, даваемой формулами (3.119). В общем случае такая постановка задачи весьма сложна.
и деформации, даваемой формулами (3.119). В общем случае такая постановка задачи весьма сложна.
Глава IV
Постоянный ток и постоянное магнитное поле.
§1 Плотность тока и проводимость.
Мы рассматривали в главах II и III электрические поля, создаваемые неподвижными зарядами. Перейдем теперь к рассмотрению стационарного движения зарядов в проводниках и полей, создаваемых этими зарядами.
В главе I средняя плотность потока зарядов или просто плотность электрического тока обозначалась буквой  (имеются в виду свободные заряды среды – проводника, сторонних зарядов нет). Предполагается, что статически распределенных (т.е. неподвижных) зарядов нет, а имеющееся пространственное распределение
(имеются в виду свободные заряды среды – проводника, сторонних зарядов нет). Предполагается, что статически распределенных (т.е. неподвижных) зарядов нет, а имеющееся пространственное распределение  не зависит от времени. Тогда в соответствии с (1.52) имеем
не зависит от времени. Тогда в соответствии с (1.52) имеем
 (4.1)
(4.1)
Электрическое поле, существующее внутри проводника, по которому течет постоянный ток, также постоянно, в соответствии с (1.50) оно удовлетворяет уравнению
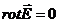 , (4.2)
, (4.2)
т.е. имеет потенциал  . К уравнениям (4.1) и (4.2) должно еще быть присоединено уравнение, связывающее
. К уравнениям (4.1) и (4.2) должно еще быть присоединено уравнение, связывающее  и
и 
 (4.3)
(4.3)
Наконец, помимо этих уравнений должны быть сформулированы граничные условия. При этом, если проводник окружен диэлектрической средой, то эти условия имеют вид
 ,
, 
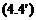
Если проводник соприкасается с другой проводящей средой, то
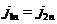 ,
,  ,
, 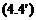
здесь индекс  означает нормальную составляющую, индекс
означает нормальную составляющую, индекс  - тангенциальную, 1 относится к данному проводнику, 2 к его окружению.
- тангенциальную, 1 относится к данному проводнику, 2 к его окружению.
В огромном большинстве случаев связь между  и
и  в материальном уравнении (4.3) – линейная (закон Ома).
в материальном уравнении (4.3) – линейная (закон Ома).
Если проводник однороден и изотропен, то линейная зависимость сводится к пропорциональности
 ,
, 
где коэффициент  - скалярная величина, зависящая от рода и состояния проводника, называется проводимостью (электропроводностью)
- скалярная величина, зависящая от рода и состояния проводника, называется проводимостью (электропроводностью)
Тогда (4.1)-(4.2), (4.3’), (4.4’), (4.4’’) запишутся
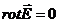
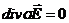 (4.5)
(4.5)
 (если окружение диэлектрик)
(если окружение диэлектрик)
или
 (если окружение проводник)
(если окружение проводник)
В однородном проводнике  и поэтому
и поэтому  . Так как
. Так как  , то потенциал электрического поля удовлетворяет уравнению Лапласа
, то потенциал электрического поля удовлетворяет уравнению Лапласа
 (4.6)
(4.6)
Можно убедиться в том, что в случае изотропного и однородного проводника 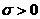 всегда. В самом деле, электрическое поле, поддерживающее ток, производит над перемещающимися в проводнике заряженными частицами механическую работу. За время
всегда. В самом деле, электрическое поле, поддерживающее ток, производит над перемещающимися в проводнике заряженными частицами механическую работу. За время  работа, производимая в единице объема, равна
работа, производимая в единице объема, равна  . Эта работа диссипируется в веществе проводника, переходя в тепло. Для изотропного и однородного проводника
. Эта работа диссипируется в веществе проводника, переходя в тепло. Для изотропного и однородного проводника
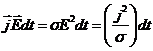 (4.7)
(4.7)
(закон Джоуля-Ленца). В процессе этого превращения работы в тепло происходит по 2-му началу термодинамики возрастания энтропии. Так как за время  в единице объема выделяется тепло
в единице объема выделяется тепло
 ,
,
а  , то
, то  . Но поскольку
. Но поскольку 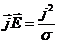 , а
, а  , то
, то 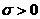 .
.
В анизотропном теле (монокристалле) направление векторов  и
и  , вообще говоря, не совпадают и линейная связь между ними выражается формулами вида
, вообще говоря, не совпадают и линейная связь между ними выражается формулами вида
 , (4.7)
, (4.7)
где  - тензор (вещественный) второго ранга, симметричный при перестановке индексов
- тензор (вещественный) второго ранга, симметричный при перестановке индексов
 (4.8)
(4.8)
Симметричность тензора  является следствием принципа симметрии кинетических коэффициентов Онзагера.
является следствием принципа симметрии кинетических коэффициентов Онзагера.
Тензор  является функцией состояния проводника. Он может зависеть от температуры и других параметров состояния. Как всякий симметричный вещественный тензор второго ранга, тензор проводимости может быть приведен к главным осям; тогда главные значения тензора
является функцией состояния проводника. Он может зависеть от температуры и других параметров состояния. Как всякий симметричный вещественный тензор второго ранга, тензор проводимости может быть приведен к главным осям; тогда главные значения тензора  (в соответствии со 2-м началом термодинамики)
(в соответствии со 2-м началом термодинамики)
Задача об определении поля и тока внутри анизотропного проводника формулируется, так же как и для случая изотропного проводника, т.е. по аналогии с (4.5). Именно
 (4.5´)
(4.5´)
Так же как и для изотропного проводника, в случай анизотропного проводника можно перейти от формулировки задачи в виде (4.5´) к формулировке задачи через потенциал 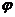
 .
.
§2 Уравнения магнитостатики
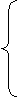 Основные уравнения магнитостатики имеют вид
Основные уравнения магнитостатики имеют вид
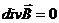 (5.1)
(5.1)
 (5.2)
(5.2)
 (5.3)
(5.3)
(5.1) и (5.2) представляют собой уравнения Максвелла в случай постоянного магнитного поля (постоянного во времени). Уравнение (5.3) есть материальное уравнение, связывающее магнитную индукцию  и напряженность магнитного поля
и напряженность магнитного поля  . Эта полная система уравнений, из которых находят 6 компонентов
. Эта полная система уравнений, из которых находят 6 компонентов  и
и  (из четырех уравнений (5.1) и (5.2) одно зависимое). Плотность тока
(из четырех уравнений (5.1) и (5.2) одно зависимое). Плотность тока  считается заданной (ее можно вычислить, решая независимую задачу, сформулированную в §1). Наряду с уравнениями (5.1)-(5.3) должны быть записаны граничные условия:
считается заданной (ее можно вычислить, решая независимую задачу, сформулированную в §1). Наряду с уравнениями (5.1)-(5.3) должны быть записаны граничные условия:
 (5.4)
(5.4)
 (5.5)
(5.5)
где 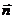 - нормаль, внешняя по отношению к первой среде,
- нормаль, внешняя по отношению к первой среде,  - поверхностная плоскость тока сторонних зарядов (если построить отрезок
- поверхностная плоскость тока сторонних зарядов (если построить отрезок  , нормальный к направлению движения заряда, текущего по поверхности, то
, нормальный к направлению движения заряда, текущего по поверхности, то  , где
, где 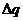 - заряд, проходящий за единицу времени через
- заряд, проходящий за единицу времени через  ), если они есть.
), если они есть.
В неферромагнитных телах, в не слишком сильных магнитных полях,  и
и  связаны друг с другом линейным соотношением. У изотропных тел линейная связь имеет вид
связаны друг с другом линейным соотношением. У изотропных тел линейная связь имеет вид
 ,
,  (5.3´)
(5.3´)
Для многих сред  , поэтому очень часто в реальных средах можно положить
, поэтому очень часто в реальных средах можно положить  . Наряду с
. Наряду с  вводят магнитную восприимчивость
вводят магнитную восприимчивость
 , (5.6)
, (5.6)
причем  может быть больше нуля, а может быть больше нуля.
может быть больше нуля, а может быть больше нуля.
Если  , то мы имеем дело со свободным магнитным полем. Ввиду
, то мы имеем дело со свободным магнитным полем. Ввиду  , значение
, значение  можно искать в виде
можно искать в виде  , т.е.
, т.е.  . Если
. Если 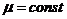 , то
, то  . На границе двух сред должны выполнятся условия
. На границе двух сред должны выполнятся условия
 , (или
, (или  )
)
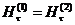
Если переписать эти граничные условия в виде условий для потенциала  (сравни с (3.6)-(3.7)), то получаем окончательно ту же задачу, что и для электростатического потенциала. Ситуация, рассмотренная в этом абзаце, имеет место, когда рассматривается область пространства, где источников поля (токов) нет, при этом граничные условия на границах этой области заданы.
(сравни с (3.6)-(3.7)), то получаем окончательно ту же задачу, что и для электростатического потенциала. Ситуация, рассмотренная в этом абзаце, имеет место, когда рассматривается область пространства, где источников поля (токов) нет, при этом граничные условия на границах этой области заданы.
§3 Магнитное поле постоянных токов.
Пусть теперь распределение токов задано. Требуется определить магнитное поле.
Из уравнения (5.1) следует, что  может быть записана в виде
может быть записана в виде
 (5.7)
(5.7)
где  - векторный потенциал. (5.7) еще не определяет
- векторный потенциал. (5.7) еще не определяет  , т.к. всякий вектор
, т.к. всякий вектор  , где
, где  - произвольная функция, также дает то же значение
- произвольная функция, также дает то же значение  , что и вектор
, что и вектор  . Поэтому не вектор
. Поэтому не вектор  можно наложить одно дополнительное условие, в качестве которого возьмем
можно наложить одно дополнительное условие, в качестве которого возьмем
 (5.8)
(5.8)
Полагая, что имеет место (5.3´), имеем
 , (5.9)
, (5.9)
Тогда (5.2) запишется
 (5.10)
(5.10)
В таком виде это уравнение справедливо для любой неоднородной среды.
В однородной среде 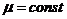 и, поскольку
и, поскольку

 ,
,
То, учитывая (5.8), имеем из (5.10)
 (5.11)
(5.11)
1. Если мы имеем две и более различных соприкасающихся сред, каждая из которых обладает своей магнитной проницаемостью  , то тогда надо записывать (5.11) для каждой из однородных сред, а на их границах должно выполнятся условие непрерывности тангенциальных компонент вектора
, то тогда надо записывать (5.11) для каждой из однородных сред, а на их границах должно выполнятся условие непрерывности тангенциальных компонент вектора  . Кроме того, должны быть непрерывны касательные компоненты самого вектора
. Кроме того, должны быть непрерывны касательные компоненты самого вектора  .
.
2. Уравнение магнитного поля токов могут быть решены в общем виде в случае однородной среды и токов, занимающих ограниченную область пространства. Последнее означает, что
 (5.12)
(5.12)
В этом случае (5.11) имеет следующее решение
 (5.13)
(5.13)
Тогда  имеет вид
имеет вид
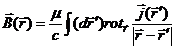
Так как
 ,
,
то
 , (5.14)
, (5.14)
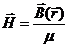
Подчеркнем, что (5.13) и (5.14) есть именно решение для однородной всюду среды (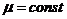 ) и при локализованных токах. В случае многослойной среды, например, это не имеет места.
) и при локализованных токах. В случае многослойной среды, например, это не имеет места.
3. Рассмотрим поле вдали от источников (расстояние до точки наблюдения много больше области, в которой локализованы токи). В этом случае
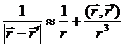
и  -я компонента потенциала запишется
-я компонента потенциала запишется
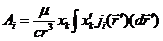
Здесь учтено, что в силу локализации источников
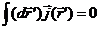
Рассмотрим тождество
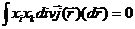
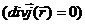
Возьмем интеграл по частям, получим
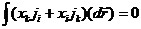
Учитывая это,  можно представить в виде
можно представить в виде
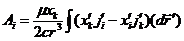
здесь  . Подинтегральная функция есть компонента векторного произведения
. Подинтегральная функция есть компонента векторного произведения  ; т.к.
; т.к.
 ,
,
где  - единичный антисимметричный тензор, то
- единичный антисимметричный тензор, то
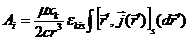
Введем обозначение
 (5.15)
(5.15)
Тогда
 (5.16)
(5.16)
Величина  называется полным магнитным моментом системы.
называется полным магнитным моментом системы.
4. Воспользуемся формулой (5.13) для получения поля линейного тока, т.е. тока тонкого проводника (его толщина мала по сравнения с длиной и расстоянием до точки, где поле определяется). Пусть уравнение, определяющее конфигурацию проводника, задано в параметрическом ( -параметр) виде
-параметр) виде
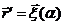
Если обозначить через  - полный ток в проводнике, то плотность тока
- полный ток в проводнике, то плотность тока  определится по формуле
определится по формуле
 (5.17)
(5.17)
Тогда имеем
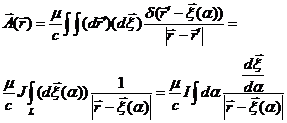 (5.18)
(5.18)
(здесь  - контур проводника)
- контур проводника)
Так в случае плоского кругового тока  ,
,  ;
;  , где
, где  - радиус кругового проводника.
- радиус кругового проводника.
Если рассмотреть поле вдали от источника тока, то удобнее пользоваться формулой (5.16), причем магнитный момент надо записать в виде, учитывающем, что ток является линейным, т.е. формулу (5.17). Подставляем в (5.15), получим
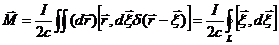
(линейный ток локализован в ограниченной области пр-ва, поэтому мы имеем замкнутый контур).
Рассмотрим  -ю компоненту момента
-ю компоненту момента
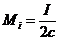
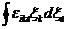
Т.к.  , где
, где  - единичный вектор в направлении
- единичный вектор в направлении  , то имеем далее
, то имеем далее
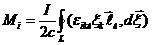
Применим теорему Стокса; тогда
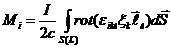
здесь  . Нормаль
. Нормаль 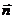 направлена таким образом по отношению к поверхности, окаймленной контуром
направлена таким образом по отношению к поверхности, окаймленной контуром  , что если смотреть с ее конца, то обход по контуру
, что если смотреть с ее конца, то обход по контуру  совершается против часовой стрелки.
совершается против часовой стрелки.
§32. Возбуждение электромагнитного поля в проводнике внешним монохроматическим излучением (токи Фуко и скин-эффект)
Рассмотрим проводник, помещенный во внешнее переменное поле с частотой 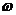 . Тогда для магнитной напряженности имеем
. Тогда для магнитной напряженности имеем
 (32.1)
(32.1)
при отсутствии проводника и
 (32.2)
(32.2)
при его наличии. Подставив (32.2) в (30.29) (30.20), мы получим уравнения для нахождения 
 внутри проводника
внутри проводника
 (
( ) (32.3)
) (32.3)
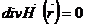 (32.4)
(32.4)
Введем характерный параметр данной задачи
 (32.5)
(32.5)
Тогда (32.3) запишется
 (32.3’)
(32.3’)
Для вычисления физического смысла величины 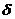 сопоставляя уравнение (30.19) с уравнением теплопроводности. Оба уравнения имеют одну и ту же структуру, причем вместо
сопоставляя уравнение (30.19) с уравнением теплопроводности. Оба уравнения имеют одну и ту же структуру, причем вместо  в уравнение теплопроводности фигурирует величина
в уравнение теплопроводности фигурирует величина  - коэффициент уравнения теплопроводности следует, что за время
- коэффициент уравнения теплопроводности следует, что за время  фиксированное значение температуры распространяется в пространстве на расстояние
фиксированное значение температуры распространяется в пространстве на расстояние  S =
S =  . Непосредственно роль
. Непосредственно роль  в уравнении (30.19) выполняет величина
в уравнении (30.19) выполняет величина
 (
(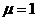 )
)
Умножим эту величину на  и извлечем квадратный корень из результата
и извлечем квадратный корень из результата
 ~
~ 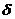
Отсюда следует, что 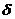 есть расстояние, на которое поле проникает в проводник за один период.
есть расстояние, на которое поле проникает в проводник за один период.
Дальнейшее решение задачи (32.3`) – (32.4) зависит от того каково соотношение между 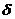 и а – размером самого проводника I. Пусть
и а – размером самого проводника I. Пусть 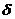 >> а. Оценим слагаемое в уравнении
>> а. Оценим слагаемое в уравнении  (32.3`), т.е. в уравнении
(32.3`), т.е. в уравнении
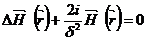
Порядок первого слагаемого ~  , порядок второго
, порядок второго  . Так как
. Так как
 , то вторым получим вместо (32.3`) и (32.4)
, то вторым получим вместо (32.3`) и (32.4)
 (32.6)
(32.6)
Но это означает, что в нулевом приближении распределение магнитного поля в каждый момент времени будет таким, каким оно было бы в стационарным случае вдали от тела. Обозначим решение системы (32.6) как  ; оно зависит частоты лишь через временной множитель
; оно зависит частоты лишь через временной множитель  . Очевидно, что
. Очевидно, что  в нулевом приближении есть
в нулевом приближении есть
 (32.7)
(32.7)
Индуцированное электрическое поле появляется лишь в следующем (первом) приближении полю, так как стационарном случае оно вообще отсутствует. В самом деле(30.18) следует в силу rot H стац. = 0


 стац.=0
стац.=0
Поэтому для вычисления  надо обратиться к уравнению rot
надо обратиться к уравнению rot  = -
= - 
 .Подставляя в него (32.7), получим, учитывая (32.1),
.Подставляя в него (32.7), получим, учитывая (32.1),
rot  (32.8)
(32.8)
div  (32.9)
(32.9)


Решим уравнение (32.8) по порядку величины E
 , т.е.
, т.е. 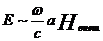
Или  (32.10)
(32.10)
II Пусть  , т.е. магнитное поле проникает лишь в тонкий поверхностный слой проводника. Для вычисления магнитного поля вне проводника можно предположить,
, т.е. магнитное поле проникает лишь в тонкий поверхностный слой проводника. Для вычисления магнитного поля вне проводника можно предположить,
Что магнитное поле в проводник не проникает вовсе. Тогда мы имеем следующие уравнения для пространства вне проводника
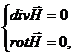
Причем поле на границе вакуум-проводник со стороны проводника равно нулю.
Хорошо известно, что если поле не проникает в образец, то этот образец есть сверх проводник, так что задача об определении поля вне проводника сводится к задаче о нахождении поля вне сверхпроводника той же формы, что и данный проводник.
Нас не будет интересовать эта задача. Будем интересоваться полем внутри проводника.
Граничные условия при решении задачи о поле внутри проводника имеют вид
 ,
,
Где  - поле на границе со стороны проводника,
- поле на границе со стороны проводника,  - поле границе со стороны вакуума, в продолжении, что вместо проводника имеем сверхпроводник той же формы.
- поле границе со стороны вакуума, в продолжении, что вместо проводника имеем сверхпроводник той же формы.
Так как поле  около сверхпроводника всегда касательно к поверхности
около сверхпроводника всегда касательно к поверхности

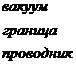
Условие (32.11) дополняет уравнения (32.3’)-(32.4), которые и подлежат решению.
Это решение можно провести в общем виде, не взирая на форму проводника, рассматривая небольшие участки поверхности как плоские.
Итак, рассмотрим задачу о падении монохроматического поля на плоскую границу проводника (см. рис).


Выберем ось Z нормально к поверхности; оси X и Y лежат в плоскости, параллельной поверхности. В силу симметрии задачи  , так что в силу (32.4)
, так что в силу (32.4)
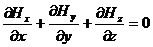
Отсюда  при любых z (в том числе при z=0). В силу (32.11) и касательного характера поля около поверхности
при любых z (в том числе при z=0). В силу (32.11) и касательного характера поля около поверхности  , так что данная
, так что данная  . Следовательно, всегда
. Следовательно, всегда
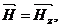
 .
.
Уравнение (32.3`) теперь запишется
 (32.12)
(32.12)
Пусть поле вне проводника около его границы есть
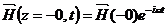
В силу (32.11) 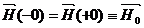
Решение уравнения (32.12) имеет вид

Имеем, что  Тогда легко увидеть, что если
Тогда легко увидеть, что если  , то слагаемое при
, то слагаемое при  в
в  так же стремится к
так же стремится к  . Поэтому
. Поэтому  . Значение
. Значение  , очевидно, равно
, очевидно, равно  . Тогда имеем решение (32.12) в виде
. Тогда имеем решение (32.12) в виде
 , (32.13)
, (32.13)
А отсюда
 (32.14)
(32.14)
Из (32.14) следует что параметр 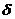 есть характерные расстояния определяющие глубину проникновения электромагнитного поля в проводник. Эффект затухания переменного поля в проводнике по мере его прохождения вглубь проводника называется скин - эффектом, а приповерхностный слой, в котором поле отлично от нуля называется скин - слоем. Чем меньше
есть характерные расстояния определяющие глубину проникновения электромагнитного поля в проводник. Эффект затухания переменного поля в проводнике по мере его прохождения вглубь проводника называется скин - эффектом, а приповерхностный слой, в котором поле отлично от нуля называется скин - слоем. Чем меньше 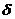 тем уже скин - слой, так что
тем уже скин - слой, так что 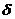 характеризует толщину скин - слоя. Из (32.5) следует, что скин - слой тем тоньше, чем выше частота поля и больше проводимость образца. В статическом и диэлектрическом пределе
характеризует толщину скин - слоя. Из (32.5) следует, что скин - слой тем тоньше, чем выше частота поля и больше проводимость образца. В статическом и диэлектрическом пределе  , т.е. скин – эффекта не наблюдается.
, т.е. скин – эффекта не наблюдается.
Найдем электрическую напряженность. В соответствии с(30.18)имеем
 (32.15)
(32.15)
Здесь 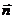 - единичный вектор в направлении оси z. Подставим (32.14) в (32.15). Получим
- единичный вектор в направлении оси z. Подставим (32.14) в (32.15). Получим 
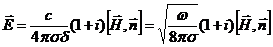 (32.16)
(32.16)
Сравним  и
и  по порядку величин
по порядку величин
E~  (32.17)
(32.17)
Где  - длина волны
- длина волны
Если поле 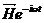 линейно поляризовано, то надлежащим выбором начала отсчета времени можно добиться вещественности
линейно поляризовано, то надлежащим выбором начала отсчета времени можно добиться вещественности 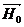 . Выберем тогда направления этого вектора вдоль оси y. Тогда для вещественных частей
. Выберем тогда направления этого вектора вдоль оси y. Тогда для вещественных частей  получим
получим
 (32.18)
(32.18)
 (32.19)
(32.19)
(здесь использовано  )
)
Вместе с электрическим полем по заказу (32.19) распределяется плотность индуцированного тока  j=
j=  (тока Фуко).
(тока Фуко).
Соотношение (32.16) в рассмотренном нами случае имеет место во всем полупространстве z=0. однако, в общих случаях соотношение вида.
 (32.20)
(32.20)
Справедливо лишь на самой поверхности проводника для тангенциальных к ней составляющих полей (в силу непрерывности этих составляющих на поверхности (32.20) имеет место по обе стороны поверхности). Коэффициент  называется поверхности импедансом проводника. В нашем случае
называется поверхности импедансом проводника. В нашем случае
 (32.21)
(32.21)
I. Возникновение токов Фуко сопровождается диссипацией энергии поля, выделяющейся в виде джоулева тепла. Средняя по времени энергия Q, диссипируемая в проводнике в 1с., равна
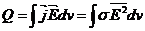
Ее можно вычислить и как среднее количество энергии поля, втекающей в 1с. извне внутрь проводника, т.е. как интервал
 (32.22)
(32.22)
взятый по поверхности проводника.
Величина  должны быть предоставлены в вещественной форме. Однако, если нас интересует среднее по времени значение произведения двух величин, то оно может быть вычислено без предварительного перехода от комплексной формы сомножителей к вещественной. В самом деле, пусть имеются две величины a(t) и b (t), записанные в комплексной форме (~
должны быть предоставлены в вещественной форме. Однако, если нас интересует среднее по времени значение произведения двух величин, то оно может быть вычислено без предварительного перехода от комплексной формы сомножителей к вещественной. В самом деле, пусть имеются две величины a(t) и b (t), записанные в комплексной форме (~ 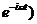
Тогда имеем
 =
=  =
= 
Очевидно
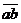 ~
~ 
 ,
, 
 ~
~ 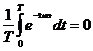
 =
=  ~
~  т.е.
т.е.
 =
=  =a
=a 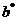 =a
=a 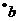
Следовательно
 =
= 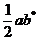 (32.23)
(32.23)
Формула (32.23) теперь может быть переписана в виде
Q=  (32.24)
(32.24)
a) Пусть  Так как амплитуда магнитного поля внутри проводника не зависит от
Так как амплитуда магнитного поля внутри проводника не зависит от  а амплитуда электрического поля ~
а амплитуда электрического поля ~  поэтому Q~
поэтому Q~ 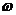
b) Пусть 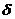 >>a. Полагая в (32.14) и (32.16) z=0 (поверхность проводника), имеем
>>a. Полагая в (32.14) и (32.16) z=0 (поверхность проводника), имеем
 (32.25)
(32.25)
Итак, для диссипации энергии имеем
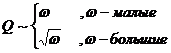
§33 Комплексное сопротивление
I. До тех пор, пока частота переменного тока достаточно мала, мгновенное значение силы тока J(t) в линейном контуре определяется значением электродвижущей силы (Э.Д.С.) 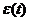 в том же момент времени согласно закону Ома
в том же момент времени согласно закону Ома
 (33.1)
(33.1)
Где R-сопротивление проводника постоянному току.
При произвольных частотах нет никаких оснований утверждать существование прямой связи между значениями ε и J в один и тот же момент времени. Можно лишь утверждать, что значение J(t) должно зависеть линейным образом от значений ε(t) во все предыдущие моменты времени, т.е.
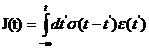
Обратная этому соотношению связь может быть записана
 (32.2)
(32.2)
Или символически
 (32.2`)
(32.2`)
Где  - некоторый линейный оператор.
- некоторый линейный оператор.
Разложим  , Z, J в (33.2) в интеграле Фурье. В частности,
, Z, J в (33.2) в интеграле Фурье. В частности,
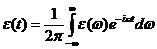
Подставляя эти разложения в (33.2) и используя
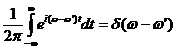
Получим для монохроматических составляющих разложений (Фурье-образов)
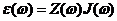 (33.3)
(33.3)
Величина Z(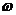 ) вообще говоря комплексна. Учитывая аналогию с (33.1), она называется комплексным сопротивлением или индексом. При чисто монохроматической зависимости
) вообще говоря комплексна. Учитывая аналогию с (33.1), она называется комплексным сопротивлением или индексом. При чисто монохроматической зависимости  и J от времени мы имеем
и J от времени мы имеем
 (33.4)
(33.4)
Так что (33.3) можно записать
 (33.3`)
(33.3`)
Из сравнения (33.3`) с (33.1) видно, что обычное сопротивление R представляет собой нулевой член разложения функции Z(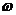 ) по степеням
) по степеням 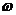 . Для определения следующего члена надо учесть наряду с R так же и самоиндукцию L проводника.
. Для определения следующего члена надо учесть наряду с R так же и самоиндукцию L проводника.
Рассмотрим линейный контур, в котором действует переменная Э.Д.С. 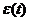 . По определению последней работа, производимая в 1с. электрическим полем над движущимся в проводе зарядами, дается произведением
. По определению последней работа, производимая в 1с. электрическим полем над движущимся в проводе зарядами, дается произведением  . Эта работа частично переходит в джоулево тепло, а частично затрачивается на изменение энергии магнитного поля тока. По определению джоулево тепло, выделяемое за 1с. в проводе, есть
. Эта работа частично переходит в джоулево тепло, а частично затрачивается на изменение энергии магнитного поля тока. По определению джоулево тепло, выделяемое за 1с. в проводе, есть  , а магнитная энергия тока есть
, а магнитная энергия тока есть  . Поэтому закон сохранения энергии выражается уравнением
. Поэтому закон сохранения энергии выражается уравнением
 (33.5)
(33.5)
Или
 (33.5`)
(33.5`)
Оперируя с  и
и  , надо писать эти величины в вещественной форме. Но если пользоваться линейным уравнением (33.5`), то
, надо писать эти величины в вещественной форме. Но если пользоваться линейным уравнением (33.5`), то  можно записать и в комплексном виде.
можно записать и в комплексном виде.
Пусть зависимость  от
от  монохроматическая (см.(33.4)). Тогда из (33.5`) и (33.4) следует
монохроматическая (см.(33.4)). Тогда из (33.5`) и (33.4) следует
 (33.6)
(33.6)
Из (33.6) следует
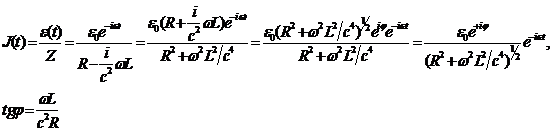 (33.7)
(33.7)
Предполагается, что Э.Д.С. задана, причем 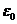 вещественна; множитель при
вещественна; множитель при  в (33.7) есть комплексная амплитуда
в (33.7) есть комплексная амплитуда  , фигурирующая в (33.4). Отделив в (33.7) вещественную часть, получим
, фигурирующая в (33.4). Отделив в (33.7) вещественную часть, получим
Вещественная часть импеданса (33.6) совпадает сопротивлением R определяющим диссипацию энергии в контуре. Легко увидеть, что и в общем случае произвольной зависимости Z ( имеется аналогичная связь между Re Z и диссипацией энергии. В самом деле. Усреднив по времени мощность
имеется аналогичная связь между Re Z и диссипацией энергии. В самом деле. Усреднив по времени мощность  потребляемую в контуре при протекании в нем периодического тока, мы найдем ту её часть, которая систематически затрагивается на покрытие диссипационных потерь. Таким образом отнесенная в 1с. диссипация энергии Q в контуре(см.(32.23))
потребляемую в контуре при протекании в нем периодического тока, мы найдем ту её часть, которая систематически затрагивается на покрытие диссипационных потерь. Таким образом отнесенная в 1с. диссипация энергии Q в контуре(см.(32.23))
Q= 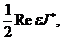
где  и J выражены в комплексном виде. Подставим сюда
и J выражены в комплексном виде. Подставим сюда  причем Z=Z`+
причем Z=Z`+  Z``
Z``
(Z`и Z``- вещественны). Имеем
Q=  (33.8)
(33.8)
Мы доказали искомую связь. Если использовать величины  в вещественной форме, то
в вещественной форме, то
 (33.8`)
(33.8`)
где 
 - вещественная функция
- вещественная функция
II. Рассмотрим контур, находящийся во внешнем переменном магнитном поле  , которое может иметь любое происхождение. Пусть
, которое может иметь любое происхождение. Пусть  - электрическое поле, индуцированное полем
- электрическое поле, индуцированное полем  , при отсутствии контура. Как
, при отсутствии контура. Как  , так и
, так и  тонкого провода. Поэтому можно рассматривать циркуляцию
тонкого провода. Поэтому можно рассматривать циркуляцию  по контуру тока, не уточняя, где именно внутри провода этот контур проведен. Это циркуляция есть что иное, как Э.Д.С.
по контуру тока, не уточняя, где именно внутри провода этот контур проведен. Это циркуляция есть что иное, как Э.Д.С.  , индуцируемая в контуре переменным внешним магнитным полем. Согласно интегральной форме уравнения Максвелла имеем
, индуцируемая в контуре переменным внешним магнитным полем. Согласно интегральной форме уравнения Максвелла имеем
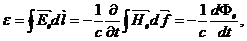
где  -поток внешнего поля через данный контур.
-поток внешнего поля через данный контур.
Не нашли, что искали? Воспользуйтесь поиском: