Задачи комбинаторного программирования

Математические модели процессов управления и организационно-технологического проектирования строительного производства предполагают решение ряда оптимизационных задач, основной особенностью которых является дискретность варьируемых параметров, то есть их область допустимых значений представляет ограниченное замкнутое множество. Действительно, процесс принятия управленческого решения чаще всего характеризуется ситуациями, которые описываются простейшими понятиями, такими как «Да» - данное решение принимается, или «Нет» - это решение должно быть отвергнуто. При описании огранизационно-технологических задач необходимо математически сформулировать условия типа: j - бригада занята выполнением работ на i -ом объекте. Формальное описание утверждений подобного типа возможно путем введения в рассмотрение дискретных переменных, то есть величин, принимающих только целые значения.

Основной особенностью задач комбинаторного программирования является существование конечного множества возможных решений. Размеры такого множества сильно зависят от общей размерности задачи и могут быть огромными, но все равно имеется некоторая верхняя граница. Это дает возможность, хотя бы чисто гипотетическую, найти оптимальное решение задачи простейшим перебором вариантов. При современных возможностях вычислительной техники это вполне возможный вариант решения задач небольшой размерности.

Рассмотрим некоторые задачи комбинаторного программирования применительно к строительному производству.

Пусть имеется N объектов, на которых необходимо выполнить один и тот же тип работ. Известна продолжительность выполнения этого вида работы на каждом из объектов , где j =1, 2,..., N, заданы директивные сроки выполнения работ на каждом из объектов и задана прибыль , получаемая фирмой за выполнение работ на этих объектах. Задача состоит в составлении такого графика движения бригады по объектам, чтобы за рассматриваемый промежуток времени прибыль составила максимальное значение.

В целях формализации задачи пронумеруем все имеющиеся объекты, расположив их в произвольном порядке. Обозначим множество номеров объектов через . Решением будет являться множество, в котором указывается последовательность номеров объектов, проходимых бригадой с максимальной прибылью для предприятия. То есть номер позиции в списке определяет номер объекта, а число, стоящее в этой позиции, - очередность. Например, запись вида {6,7,4,...,1} означает, что первый объект будет выполнен 6-м, второй - 7-м, третий - 4-м, а последний объект необходимо выполнить в первую очередь. Таким образом, множество представляет собой перестановки элементов множества .

Целевая функция представляет собой доход от выполнения работ в заданные директивные сроки, причем бригада в каждый момент времени может работать только на одном объекте. Таким образом, календарный срок окончания работ на r -ом объекте будет представлять собой сумму продолжительностей работ на предыдущих r -1 объектах. С учетом этого пояснения целевую функцию можно будет записать в виде

, (7.10.1)

где - единичная функция импульсного типа, то есть, когда аргумент отрицательный (это соответствует практической ситуации, когда срок выполнения работ на объекте уже просрочен), она равна нулю (вознаграждение отсутствует), а при положительных значениях - 1.

Для каждой очередности функция (7.10.1) определяет величину суммарного штрафа за нарушение директивных сроков. Таким образом, задача состоит в поиске на множестве минимума функции . Рассмотрим конкретный пример сформулированной задачи, для которого все 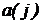равны 1 (т.е. определяет для очередности число заданий, не выполненных к директивным срокам). Длительности и директивные сроки T (j) представлены в табл.7.10.1 (число заданий равно 8).

Таблица 7.10.1

j
T(j)

Покажем, что значения целевой функции существенно зависят от выбранной очередности . Для этого подсчитаем для двух перестановок (очередностей) :

=(1,2,3,4,5,6,7,8), =(5,4,3,2,7,1,8,6).

Легко проверить, что для очередности оказываются нарушенными директивные сроки для заданий с номерами 3,4,5,6,7,8, а для очередности - только с номерами 8 и 6. Таким образом, .

Задачи определения порядка обработки деталей. При организации технологического процесса обработки деталей возникает проблема выбора порядка запуска деталей в производство. Проблема состоит в том, чтобы при заданных временах и последовательностях обработки найти такой порядок запуска деталей, при котором суммарное время обработки минимально. При формализации этой задачи будем использовать введенные выше обозначения в несколько иной интерпретации:

множество деталей, подлежащих обработке; - перестановка из элементов множества , задающая порядок запуска деталей в производство; - множество номеров станков, число которых равно М. При формализации, кроме того, делаются следующие естественные во многих случаях предположения:

1) каждая из деталей должна быть обработана на каждом из М станков;

2) начавшись, обработка любой детали доводится до конца без перерывов;

3) последовательность прохождения деталей по станкам одинакова для всех деталей. Примем для определенности, что нумерация станков соответствует последовательности обработки деталей (последнее означает, что любая деталь с номером k до завершения ее обработки на всех станках с номерами, меньшими k);

4)заданы времена обработки j -ой детали на i -ом истанке ().С учетом сделанных предположений введенных обозначенийможно для каждого порядка запуска деталей определить времена завершения обработки детали на первых k станках. Для k =1 величины определяются следующим образом:

. (7.10.2)

Далее для j =1 имеем при всех :

. (7.10.3)

Что касается величин в общем случае, то они могут быть определены рекуррентно через величины , а именно:

. (7.10.4)

При вычислениях по формуле (7.10.4) для каждого k индекс j приобретает значения 2, 3,..., N, а сам индекс k принимает последовательно значения 2.3...., M. Соотношение (7.10.4) получается из следующего простого соображения: обработка детали на k -ом станке может начаться только по окончании обработки на k -ом станке детали , предшествующей в очередности детали .

Критерий оптимальности в задачах определения порядка обработки деталей обычно связан с временем выполнения обработки всех деталей на всех станках, которое стремятся, по возможности, уменьшить. Поэтому в качестве целевой функции может быть выбрано зависящее от время окончания обработки детали на станке М:

. (7.10.5)

Множеством возможных решений в рассматриваемой задаче является , на котором и определена с помощью (7.10.2)-(7.10.5) целевая функция . Итак, формальная постановка задачи такова: на множестве найти перестановку, минимизирующую функцию .

Проиллюстрируем данную постановку на конкретных числовых данных. Зададим N = 5, M =2, а величины в табл. 7.10.2.

Таблица 7.10.2.

Рассмотрим два порядка обработки :

=(1,2,3,4,5), =(3,5,4,2,1).

Процесс обработки при порядках схематически изображен на диаграммах рис.1. Из рис. видно, что =16.

Тот же результат получится при вычислениях по формулам (7.10.2)-(7.10.5).

Вопросы для повторения

1. Зависимость графика линейной функции от углового ко­эффициента.

2. Виды нелинейных функций, их графики. Линия уровня.

3. Свойства функций и множеств, их экономическая интер­претация.

4. Функции многих переменных. Содержательная интерпре­тация производной и дифференциала функции. Градиент, мат­рица Гессе, их свойства и применение в экономике.

5. Экстремальные задачи. Условия существования оптимальных решений. Необходимые и достаточные признаки оптимальности.

6. Задачи нелинейного программирования. Метод множите­лей Лагранжа.

7. Задачи линейного программирования. Алгоритм симплекс-метода.

8. Численные характеристики дискретных случайных вели­чин и их свойства.

Контрольные упражнения и задачи

2.1. Показать, что функция у =ln х строго возрастает.

2.2. Пользуясь определением, показать, что функция

является выпуклой.

2.3. Убедиться в выпуклости во всем пространстве R³ функции

и найти точки ее экстремума.

2.4. Решить задачу линейного программирования

f (х) = 2 х ₁ - 3 х ₂ + 6 х ₃ + х ₄ → max

при ограничениях

x_i ≥ 0, i =1,…,4

симплекс-методом или двухфазным симплекс-методом.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ И ДИСКУССИЙ

1. Каковы особенности задач линейного программирования?

2. Какое решение системы линейных уравнений является планом?

3. В чем суть решения задачи симплекс - методом?

4. Какой опорный план называется вырожденным, невырожденным?

5. Как привести задачу линейного программирования к канонической форме?

6. Какие задачи производственной деятельности можно представить в виде линейного, нелинейного и динамического программирования?

7. Какие показатели производственной деятельности предприятий имеют линейную, нелинейную форму связи?

8. Какие задачи линейного программирования можно решать симплексным методом?

9. Каков признак оптимальности в симплекс-методе?

10. Каковы основные случаи при реализации симплекс-метода?

11. В каких вариантах постановки задач следует пользоваться для их решения методом искусственного базиса?

12. Как осуществляется перерасчет элементов симплексной таблицы?

13. Как определяется ведущий столбец и ведущая строка симплексной таблицы?

14. Какие функции называются унимодальными?

15. Каковы недостатки классического метода решения задач оптимизации?

Не нашли, что искали? Воспользуйтесь поиском: