Привести уравнение Бернулли и пояснить его применение на практическом примере.

Рассмотрим стационарное течение жидкости.

При перемещении некоторой массы жидкости ∆m из одного сечения трубы во второе ее скорость, а значит, и кинетическая энергия изменяются.

Внешними силами, которые действуют на эту массу жидкости, являются ее сила тяжести ∆mg и силы давления со стороны жидкости, которая находится позади этой массы, F₁=p₁S₁ и со стороны жидкости, находящейся перед ней, F₂=p₂S₂.

Если рассматривать эту массу в качестве физической системы, которая находится в инерциальной системе отсчета, связанной с поверхностью Земли, то изменение кинетической энергии рассматриваемой массы жидкости согласно теореме об изменении кинетической энергии равно сумме работ силы тяжести и сил давления, т. е.

,

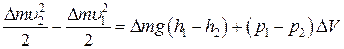где ∆V - объем жидкости, переместившейся за некоторый интервал времени с участка трубы сечением S₁ и давлением p₁ на другой участок трубы сечением S₂ и давлением p₂; υ₁ и υ₂ - скорости течения жидкости в рассматриваемых сечениях; h₁ и h₂ - высоты центра тяжести выделенной массы жидкости относительно некоторого нулевого горизонтального уровня.

После деления левой и правой частей полученного равенства на объем ∆V получим:

.

Так как сечения S₁ и S₂ взяты произвольно, то для любого сечения трубки тока:

(*).

Полученное соотношение (*) называют уравнением Бернулли, согласно которому при стационарном течении идеальной жидкости сумма ее статического и динамического давлений постоянна в любом сечении трубы.

Из уравнения Бернулли следует, что при увеличении скорости течения (уменьшении сечения трубы) динамическое давление жидкости возрастает, а ее статическое давление уменьшается.

Практическое применение уравнения Бернулли:

1) Водомер Вентури представляет собой короткий от­резок трубы с сужением посредине. В широкой части и гор­ловине устанавливаются либо пьезометры, либо дифференциаль­ный манометр.

2) Карбюратор поршневых двигателей внутреннего сго­рания служит для осуществления подачи бензина и смешения его с потоком воздуха. Поток воздуха, засасываемый в дви­гатель, сужается там, где установлен распылитель бензина. Скорость воздуха в этом сечении возрастает, а давление по уравнению Бернулли падает.

3) Трубка Пито широко применяется для измерения скорости воды и газа.

Задача 4

Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом. Найти динамическую и кинематическую вязкости касторового масла, если шарик всплывает с постоянной скоростью 3,5 см/с.

Дано:

Решение.

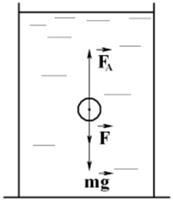
По второму закону Ньютона имеем: .

В проекции на вертикальную ось, направленную вверх имеем: .

Сила Архимеда равна: , где - объем шарика,

- плотность касторового масла.

Тогда,

Сила Стокса равна: .

Масса шарика равна: , где - плотность пробки.

Значит, динамическая вязкость равна:

,

.

Кинематическая вязкость определяется по формуле: .

Получаем, ,

.

Ответ. , .

Ответить на теоретические вопросы:

Не нашли, что искали? Воспользуйтесь поиском: