Теоремы о дифференцируемых функциях

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒

Определение. Точка называется точкой максимума (минимума), если существует такая окрестность этой точки, что для любой точки 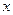этой окрестности выполняется неравенство: ().

Теорема Ферма.

Пусть функция определена в некоторой окрестности точки и принимает в этой точке наибольшее или наименьшее значение. Тогда, если при 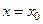существует производная, то она равна нулю ().

Теорема Ролля.

Если функция непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и принимает на концах отрезка [a,b] равные значения , то на интервале (a,b) найдется хотя бы одна точка , в которой производная равна нулю: , .

Следствие. Если функция непрерывна на некотором отрезке, обращается в ноль на его концах и дифференцируема во всех его внутренних точках, то существует его внутренняя точка, в которой производная обращается в ноль. Коротко говоря, между двумя нулями дифференцируемой функции всегда лежит хотя бы один ноль ее производной.

Теорема Лагранжа.

Если функция непрерывна на отрезке [a,b], дифференцируема во всех его внутренних точках, то найдется хотя бы одна точка , что справедлива формула .

Эту формулу называют формулой конечных приращений Лагранжа.

Теорема Коши.

Если функции и непрерывны на отрезке [a,b] и дифференцируемы во всех его внутренних точках, причем не обращается в 0, то найдется хотя бы одна точка такая, что справедлива формула

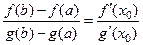, (формула Коши).

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2025 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных