Приложения определенного интеграла к решению некоторых задач механики и физики

Пусть в точках с координатами (x₁, y₁), (x₂ y₂),…, (x_n, y_n) сосредоточены точечные массы m₁, m₂,…, m_n.

Статическим моментом данной системы материальных точек относительно оси Ox называется число, определяемое равенством .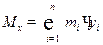

Статическим моментом данной системы материальных точек относительно оси Oy называется число, определяемое равенством .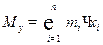

Центром масс данной системы материальных точек называется точка (x_c, y_c), обладающая тем свойством, что если в ней сосредоточить всю массу системы, то ее статические моменты относительно координатных осей будут равны соответствующим статическим моментам всей системы, то есть

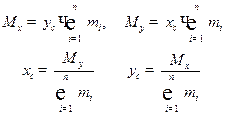
Моментом инерции данной системы материальных точек относительно оси Ox называется число, определяемое равенством .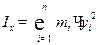

Моментом инерции данной системы материальных точек относительно оси Oy называется число, определяемое равенством .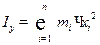

Если дуга кривой задана уравнением 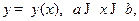и имеет плотность (масса на единицу длины) 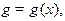то статические моменты этой дуги M_x и M_y относительно координатных осей Ox и Oy равны

моменты инерции I_x и I_y относительно тех же осей Ox и Oy вычисляются по формулам

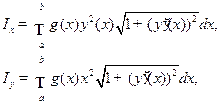
а координаты центра масс x_c и y_c - по формулам

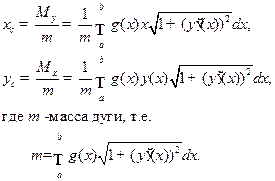
С помощью определенного интеграла можно находить также массу, статические моменты, моменты инерции, координаты центра масс однородных (с постоянной плотностью) плоских фигур.

Если плоская фигура ограничена кривой y=y(x), прямыми x=a, x=b и осью Ox, имеет плотность 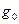, то

масса фигуры вычисляется по формуле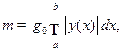

статические моменты -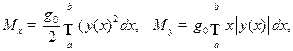

моменты инерции -

координаты центра масс -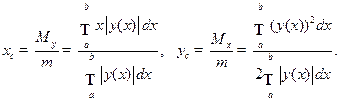

В приложениях часто оказываются полезными следующие теоремы

Первая теорема Гульдена. Площадь поверхности, полученной при вращении плоской однородной дуги вокруг некоторой оси, лежащей в той же плоскости и не пересекающей дугу, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

Вторая теорема Гульдена. Объем тела, полученного при вращении плоской однородной фигуры вокруг некоторой оси, лежащей в плоскости этой фигуры и не пересекающей ее, равен произведению площади фигуры на длину окружности, описываемой ее центром масс.

Например.

Не нашли, что искали? Воспользуйтесь поиском: