
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
КОНТРОЛЬНОЙ РАБОТЫ №2
6 Вычислить площадь фигуры, ограниченной заданными параболами  .
.
Решение.
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:
 .
.
Отсюда 
 .
.
 |
у
–1 0 1 х
Площадь вычислим по формуле
 ,
,
где  ,
,  – кривые, ограничивающие фигуру (
– кривые, ограничивающие фигуру (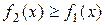 ).
).
В нашем случае

 (ед3).
(ед3).
7. Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой  , прямой
, прямой  и осью Ох.
и осью Ох.
Решение.
Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение
 ,
,
 ,
,
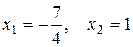 .
.
Первому квадранту соответствует корень  .
.
Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение  , откуда
, откуда  .
.
 Таким образом, можно считать, что тело вращения ограничено при
Таким образом, можно считать, что тело вращения ограничено при  поверхностью, образованной вращением параболы
поверхностью, образованной вращением параболы  вокруг оси Ох, а при
вокруг оси Ох, а при  – вращением прямой
– вращением прямой  .
.
у
0 2 х
Объем ищем по формуле
 .
.
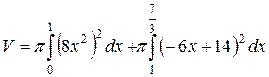 .
.
Для вычисления второго интеграла используем подстановку  . Тогда
. Тогда  и
и  .
.
Отсюда
 (ед3).
(ед3).
8. Найти общее решение дифференциальных уравнений первого порядка.
а) 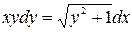 ; б)
; б)  .
.
Решение.
а) Данное уравнение является уравнением с разделяющимися переменными. Разделив левую и правую части уравнения на выражение  (при
(при  ), приходим к равенству
), приходим к равенству
 .
.
Интегрируя, получим

или
 ,
,
так как интеграл в правой части табличный, а интеграл в левой части найдем заменой переменной:
 .
.
 – общий интеграл дифференциального уравнения.
– общий интеграл дифференциального уравнения.
б) Данное уравнение также является уравнением с разделяющимися переменными. Представим производную в виде отношения дифференциалов  и умножим обе части уравнения на
и умножим обе части уравнения на 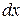 :
:

Теперь разделим обе части равенства на множитель  :
:
 .
.
Интегрируем обе части равенства:

Интегралы в левой и правой частях равенства найдем заменой переменной


Константу в правой части равенства возьмем в виде  , получаем:
, получаем:
 .
.
Используя свойство логарифмов  , имеем:
, имеем:
 .
.
Потенцируя, получим общее решение уравнения:  .
.
9. 1) Найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
а)  , б)
, б)  ,
,
в)  , г)
, г)  .
.
2) Найти частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами  , удовлетворяющее указанным начальным условиям
, удовлетворяющее указанным начальным условиям  .
.
Решение.
1) Линейному однородному дифференциальному уравнению второго порядка с постоянными коэффициентами  ставится в соответствие характеристическое уравнение:
ставится в соответствие характеристическое уравнение:
 ,
,
где  – переменная.
– переменная.
1. Если характеристическое уравнение имеет действительные корни  и
и  , причем
, причем  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 .
.
2. Если характеристическое уравнение имеет два совпадающих корня  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 .
.
3. Если характеристическое уравнение имеет комплексные корни  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 .
.
а)  . Составляем характеристическое уравнение
. Составляем характеристическое уравнение  . Корнями этого уравнения будут
. Корнями этого уравнения будут  и
и  . Корни действительные и различные, тогда получаем общее решение:
. Корни действительные и различные, тогда получаем общее решение:
 .
.
б)  . Составляем характеристическое уравнение
. Составляем характеристическое уравнение  . Решая это уравнение, получим совпадающие корни
. Решая это уравнение, получим совпадающие корни  . Тогда общее решение:
. Тогда общее решение:
 .
.
в)  . Характеристическое уравнение
. Характеристическое уравнение  имеет комплексные корни:
имеет комплексные корни:

Отсюда  и общее решение:
и общее решение:
 .
.
г)  . Решаем характеристическое уравнение
. Решаем характеристическое уравнение  :
:

Отсюда  , получим общее решение:
, получим общее решение:
 .
.
2)  . Составляем характеристическое уравнение
. Составляем характеристическое уравнение  . Корни этого уравнения
. Корни этого уравнения  . Так как корни действительные и совпадающие, то общее решение имеет вид:
. Так как корни действительные и совпадающие, то общее решение имеет вид:
 .
.
Найдем частное решение, удовлетворяющее условиям: 
 . Продифференцируем общее решение:
. Продифференцируем общее решение:
 .
.
Подставляя значения  при
при  в выражения для у и
в выражения для у и  , получаем:
, получаем:

Искомое частное решение:
 .
.
10. Найти область сходимости степенного ряда  .
.
Решение. Общий член ряда  . Для исследования ряда на сходимость применим признак Даламбера:
. Для исследования ряда на сходимость применим признак Даламбера:
 .
.
Таким образом, при  , то есть при
, то есть при 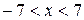 исходный ряд сходится абсолютно.
исходный ряд сходится абсолютно.
Выясним вопрос о сходимости ряда на концах интервала сходимости. При  заданный ряд принимает вид
заданный ряд принимает вид
 .
.
Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при  . Таким образом, оба условия признака Лейбница выполнены и ряд сходится, то есть точка
. Таким образом, оба условия признака Лейбница выполнены и ряд сходится, то есть точка  принадлежит области сходимости заданного степенного ряда.
принадлежит области сходимости заданного степенного ряда.
При  исходный ряд принимает вид
исходный ряд принимает вид
 .
.
Это числовой знакоположительный ряд, который расходится (сравните его с гармоническим рядом  . Следовательно, точка
. Следовательно, точка  не принадлежит области сходимости заданного степенного ряда.
не принадлежит области сходимости заданного степенного ряда.
Таким образом, область сходимости исходного степенного ряда 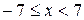 . Вне этого интервала ряд расходится.
. Вне этого интервала ряд расходится.
11. Дана функция двух переменных  . Найти:
. Найти:
1) экстремум функции  ;
;
2)  в точке А (1; –2);
в точке А (1; –2);
3) наибольшую скорость возрастания  точке А (1; –2).
точке А (1; –2).
Решение. 1) Для отыскания экстремума функции  предварительно найдем частные производные первого и второго порядка:
предварительно найдем частные производные первого и второго порядка:
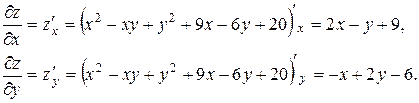
Приравняем их к нулю и решим систему уравнений:

Решением системы является точка М (–4; 1). Точка М (–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:

Из них составим определитель второго порядка

Так как  , то в точке М (–4; 1) есть экстремум. Производная
, то в точке М (–4; 1) есть экстремум. Производная  , а, значит, это точка минимума функции.
, а, значит, это точка минимума функции.
2) Градиент функции  найдем по формуле:
найдем по формуле:
 ,
,
 и
и  были найдены в пункте 1.
были найдены в пункте 1.
 .
.
Градиент функции  в точке А (1; –2):
в точке А (1; –2):
 .
.
3) Наибольшая скорость возрастания функции равна модулю градиента:
 .
.
12. Дан интеграл  . Требуется построить на плоскости хОу область интегрирования D и вычислить площадь области D при помощи данного интеграла.
. Требуется построить на плоскости хОу область интегрирования D и вычислить площадь области D при помощи данного интеграла.
Решение. Пределы внешнего интеграла по переменной х – числа 1 и 3 – указывают на то, что область D ограничена слева прямой  и справа прямой
и справа прямой  .
.
 Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу параболой
Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу параболой  и сверху прямой
и сверху прямой  . Построив эти линии на отрезке
. Построив эти линии на отрезке  , получим область D (рисунок 12.1).
, получим область D (рисунок 12.1).
у
5 В
1 А
0 1 3 х
Рисунок 12.1
Вычислим площадь области D при заданном порядке интегрирования:

13. Вероятность того, что семя злака прорастет, равна 0,6. Найти вероятность того, что из 150 посеянных семян прорастет ровно 102 семени.
Решение. Если вероятность наступления события А в каждом из п независимых испытаний постоянна и равна р, а число п достаточно велико, то вероятность  того, что в этих испытаниях событие А наступит ровно
того, что в этих испытаниях событие А наступит ровно  раз, вычисляется приближенно по формуле, которая выражает локальную теорему Лапласа:
раз, вычисляется приближенно по формуле, которая выражает локальную теорему Лапласа:
 , где
, где  .
.
Значения функции  даны в таблице 1 приложения. Для значений
даны в таблице 1 приложения. Для значений  считают
считают  . Если
. Если  , то
, то  , так как эта функция четная.
, так как эта функция четная.
По условию задачи  . Вычислим х:
. Вычислим х:
 .
.
По таблице значений функции  находим
находим 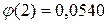 . Тогда искомая вероятность равна
. Тогда искомая вероятность равна
 .
.
14. Измерены диаметры  для 60 деталей, обрабатываемых на некотором станке. Данные замеров приведены в таблице 1.
для 60 деталей, обрабатываемых на некотором станке. Данные замеров приведены в таблице 1.
Таблица 1
| 70,88 | 67,04 | 69,20 | 66,24 | 64,80 | 71,52 | 67,52 | 68,96 | 67,36 | 68,64 |
| 67,12 | 66,96 | 69,04 | 66,00 | 66,00 | 64,88 | 65,84 | 67,52 | 65,68 | 70,00 |
| 70,80 | 66,32 | 67,40 | 66,08 | 69,76 | 68,01 | 65,76 | 69,20 | 65,60 | 66,72 |
| 67,44 | 67,72 | 68,72 | 64,00 | 66,32 | 68,21 | 70,96 | 67,76 | 66,88 | 69,12 |
| 65,84 | 64,88 | 69,46 | 68,48 | 65,04 | 70,00 | 70,16 | 68,72 | 67,04 | 69,36 |
| 66,48 | 68,20 | 64,72 | 70,40 | 67,76 | 69,28 | 71,20 | 67,90 | 66,80 | 70,24 |
Выполнить статистическую обработку результатов измерений по следующему плану:
1) Построить статистическое распределение выборки.
2) Выполнить точечные оценки среднего значения  и дисперсии
и дисперсии  случайной величины
случайной величины  .
.
3) Построить гистограмму относительных частот, установив статистический (эмпирический закон распределения).
4) На том же чертеже построить кривую нормального распределения с параметрами  и
и  и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.
и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.
Не нашли, что искали? Воспользуйтесь поиском: