ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА СВЕДЕНИЕМ К ПОВТОРНОМУ ИНТЕГРАЛУ

Вычисление двойного интеграла в декартовой системе координат от функции по области можно выполнить в соответствии со следующими теоремами.

Теорема 1 ( о сведении двойного интеграла к повторному). Если область интегрирования – криволинейная трапеция, ограниченная сверху и снизу непрерывными кривыми 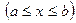, а подынтегральная функция непрерывна в области (см. рис. 2 ), то двойной интеграл сводится к повторному по формуле

. (2)

В этом случае область D называют нормальной по х (см. рис. 2).

Теорема 2 ( о сведении двойного интеграла к повторному). Если область интегрирования – криволинейная трапеция, ограниченная слева и справа непрерывными кривыми , а подынтегральная функция непрерывна в области , то двойной интеграл сводится к повторному по формуле

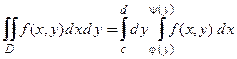. (3)

В этом случае область D называют нормальной по у (см. рис. 3).

С л е д с т в и е. Если область интегрирования – прямоугольник, заключенный между прямыми а подынтегральная функция непрерывна в области , то двойной интеграл

(4)

В формуле (2) интеграл называют повторным. Сначала вычисляют внутренний интеграл при постоянном значении , затем полученную в ходе интегрирования функцию переменной x подставляют во внешний интеграл и выполняют ее интегрирование в пределах от a до b. Аналогичным образом поступают при вычислении интегралов по формулам (3) и (4), при этом интегралы в правых частях этих формул также называют повторными.

Если область D не является криволинейной трапецией, то ее разбивают на несколько частей, являющихся криволинейными трапециями. Тогда искомый интеграл является суммой двойных интегралов, распространенных на отдельно взятые части.

Пример 2. Вычислить повторный интеграл

□ Как сказано выше, вычисления следует начинать с нахождения внутреннего интеграла:

Полученную функцию подставим во внешний интеграл:

Отсюда, ■

Рассмотрим две плоскости , в которых введены декартовы системы ко

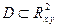и с границей . Пусть в плоскости определены дифференцируемые функции

(5)

такие, что когда точка пробегает область 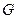, то соответствующая точка пробегает область . Тогда соотношения (5) задают отображение множества 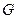на множество .

Если в каждой точке области 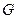дифференцируемые функции удовлетворяют условию (за исключением, быть может, конечного числа точек), то рассматриваемое отображение обладает следующими свойствами.

1. Оно взаимно однозначно отображает 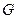на : каждой точке по

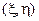формулам (5) соответствует только одна точка ; различным точкам отвечают различные точки .

2. Переменные являются однозначными функциями от в области D:

(6)

т.е. система (5) однозначно разрешима относительно .

3. Внутренним точкам (и внутренности) множества 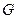соответствуют внутренние

точки (и внутренность) множества , а граничным точкам (и границе множества) 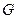соответствуют граничные точки (и граница) множества .

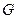Будем говорить, что области связаны соотношениями и называть область образом области , а область 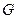− прообразом области .

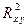Соотношения (6) позволяют к каждой точке области привязать единственным образом пару чисел , которые можно назвать криволинейными координатами точки. Так, например, значению в соответствует координатная линия, заданная уравнениями , которые можно рассматривать как параметрические уравнения этой, вообще говоря, кривой линии (роль параметра выполняет переменная ). Совокупность всех координатных линий образует координатную сетку в плоскости 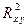(см. рис. 4). Поэтому формулы можно толковать не только как формулы, определяющие связи между системами координат в разных плоскостях, но и как формулы, связывающие декартову и криволинейную системы координат в одной и той же плоскости .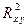

Определитель называют якобианом отображения (преобразования). Его абсолютная величина равна коэффициенту растяжения области в данной точке при указанном преобразовании: . Здесь: − квадрат со стороной в плоскости , ограниченный координатными линиями, − его площадь; − это образ квадрата при данном отображении, − его площадь.

Не нашли, что искали? Воспользуйтесь поиском: