
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
по теме 2 "ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ"
2.1.1. Построить на плоскости x O y область D, ограниченную заданными линиями  ,
,  , и вычислить площадь этой области с помощью двойного интеграла.
, и вычислить площадь этой области с помощью двойного интеграла.
Решение. Изобразим область D на чертеже:

Площадь фигуры вычислим с помощью двойного интеграла по формуле:

Заметим, что 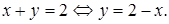
Таким образом:

 ед. кв.
ед. кв.
Ответ: 1,25 ед. кв.
2.2.1. Вычислить с помощью перехода к полярным координатам двойной интеграл 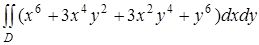 по указанной области D: D -круг
по указанной области D: D -круг  .
.
Решение. Перейдем к полярным координатам:

В полярных координатах круг  имеет уравнение
имеет уравнение  .
.
Преобразуем подынтегральное выражение:
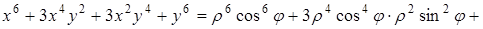

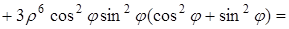


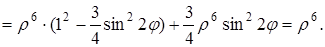
Следовательно,


Ответ: 
2.3.1. Вычислить данный тройной интеграл  , предварительно построив область интегрирования R: x =0, x =1, y =0, y =2, z =0, z =3.
, предварительно построив область интегрирования R: x =0, x =1, y =0, y =2, z =0, z =3.
Решение. Построим область интегрирования R
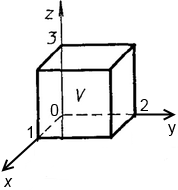
Для данной области R получаем




Ответ: 54.
2.4.1. Вычислить с помощью тройного интеграла объем тела R, ограниченного заданными поверхностями: x + y + z =6, x =0, y =0, z =0, x +2 y =4. Сделать чертеж данного тела R.
Решение. Изобразим тело R. Оно ограничено с боков координатными плоскостями x =0, y =0 и плоскостью x +2 y =4, снизу плоскостью z =0, сверху – плоскостью x + y + z =6.
Проекцией области R на плоскость хоу является прямоугольный треугольник, определяемый системой неравенств

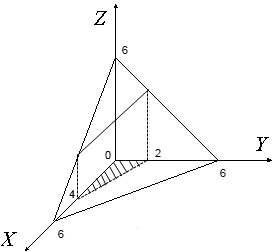
Тогда



 ед. куб.
ед. куб.
Ответ: 16 ед. куб.
2.5.1. Вычислить координаты центра тяжести однородного тела R, ограниченного указанными поверхностями: z =1- x 2- y 2, z =0. Принять плотность r =1. Сделать чертеж.
Решение. Построим тело, ограниченное параболоидом z =1- x 2- y 2 и плоскостью z =0.

Так как тело R однородное и симметричное относительно оси Oz, то можно сразу записать, что  и
и  .
.
Найдем

Полагая r =1, получаем

Проекция тела R на плоскость xOу представляет собой круг, ограниченный окружностью 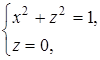 поэтому вычисления проводим в цилиндрических координатах:
поэтому вычисления проводим в цилиндрических координатах:

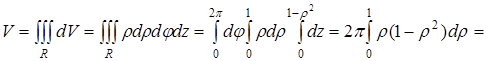
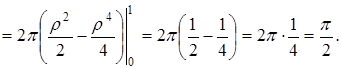


Отсюда

Центр тяжести имеет координаты С(0, 0,  ).
).
Ответ: С(0, 0,  ).
).
2.6.1. Вычислить данный криволинейный интеграл первого рода  , гдеГ – часть окружности
, гдеГ – часть окружности 
Решение. Вычисление криволинейного интеграла 1-го рода может быть сведено к вычислению определенного интеграла, причем способ такого сведения зависит от представления кривой интегрирования Г.
Если кривая Г задана параметрическими уравнениями  , a £ t £ b, то
, a £ t £ b, то 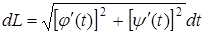 , и тогда
, и тогда
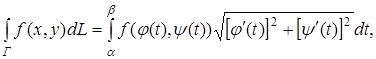
Преобразуя криволинейный интеграл к определенному, получаем:
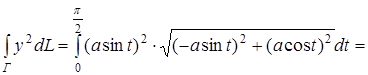
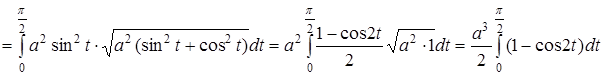

Ответ: 
2.7.1. Вычислить данный криволинейный интеграл второго рода 
где AB – четверть окружности  А при t = 0, B при
А при t = 0, B при 
Решение. Если плоская кривая Г задана параметрическими уравнениями
 a £ t £ b,
a £ t £ b,
причем установленное по кривой Г движение от А к В соответствует изменению переменной t от a до b, то

Поэтому


Ответ: 0.
Контрольная работа
по теме 4 "ТЕОРИЯ ВЕРОЯТНОСТЕЙ"
4.1.1. По самолету производится два выстрела, вероятность попадания при каждом выстреле равна 0,6. При одном попадании самолет будет сбит с вероятностью 0,5, при двух – с вероятностью 0,9. Какова вероятность, что самолет будет сбит?
Решение. Событие А – самолет сбит.
Введем гипотезы:
 было получено одно попадание в самолет;
было получено одно попадание в самолет;
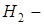 было получено два попадания в самолет;
было получено два попадания в самолет;
 самолет сбит третьей зениткой.
самолет сбит третьей зениткой.
Вероятности гипотез равны соответственно


Условные вероятности события А известны из условия задачи


Тогда по формуле полной вероятности получаем:

Ответ: 0,84.
4.2.1. Электрические цепи между точками М и N составлены по схемам, изображенным на рисунках, и состоят из нескольких узлов, в каждом из которых ni элементов. Выход из строя одного элемента означает выход из строя всего узла. Элементы выходят из строя независимо друг от друга. Прибор может случайным образом работать в одном из двух режимов: благоприятном и неблагоприятном. В благоприятном режиме надежность, т.е. вероятность безотказной работы за время Т, каждого из элементов одна и та же и равна 0,8, в неблагоприятном – 0,3. Вероятность того, что цепь находится в благоприятном режиме равна 0,8. Определить полную (среднюю) надежность электрической цепи при указанном на схеме количестве элементов в узлах.

Решение. Будем считать, что ni – это числа, стоящие в прямоугольниках.
Введем событие А – электрическая цепь работает надежно.
Гипотезы:
 прибор работает в благоприятном режиме;
прибор работает в благоприятном режиме;
 прибор работает в неблагоприятном режиме;
прибор работает в неблагоприятном режиме;
Вероятности гипотез равны соответственно


Обозначим через  событие, состоящее в работе без отказа k -го узла, k = 1,2,3,4,5,6.
событие, состоящее в работе без отказа k -го узла, k = 1,2,3,4,5,6.
Учитывая количество входящих в узлы элементов, а также строение цепи, получаем следующую формулу, описывающую безотказную работу цепи

Тогда



Учитывая, что вероятность безотказной работы за время Т, каждого из элементов одна и та же, обозначим ее через р. Имеем

Тогда условные вероятности события А равны:
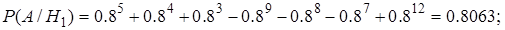

По формуле полной вероятности получаем:

Ответ: средняя надежность 0,6525.
4.3.1. Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено не более трех изделий.
Решение. n= 1000, p= 0,002.
Применим формулу Пуассона:

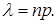
По условию имеем: 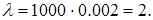
Искомая вероятность


Ответ: 0,8571.
4.4.1. Закон распределения дискретной случайной величины X задан следующей таблицей:
| X | ||||
| P | 1/16 | 1/4 | 1/2 | 3/16 |
Найти М (Х), s(Х) и Р (Х >2).
Решение. Математическое ожидание:

Дисперсия:


Среднее квадратическое отклонение

Искомая вероятность равна:

4.5.1. Случайная величина Х имеет плотность  . Найти коэффициент А, функцию распределения F (х), вероятность неравенств –1< X <1, M (X).
. Найти коэффициент А, функцию распределения F (х), вероятность неравенств –1< X <1, M (X).
Решение. Пользуясь свойством нормировки дифференциальной функции распределения, найдем значение параметра А:


Следовательно, 
По определению  .
.
Находим:


Вероятность того, что случайная величина X примет значение, заключенное в интервале 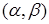 равна
равна

Находим


Математическое ожидание  непрерывной случайной величины, которая имеет четную функцию плотности распределения вероятностей, равно нулю:
непрерывной случайной величины, которая имеет четную функцию плотности распределения вероятностей, равно нулю:

4.6.1. Вероятность появления события в каждом испытании постоянна и равна 0,8. Произведено 900 испытаний. Какова вероятность того, что отклонение относительной частоты появления события от вероятности 0,8 по абсолютной величине не превзойдет 0,05?
Решение. По условию:
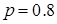 ,
, 


Для решения воспользуемся формулой:

Находим:
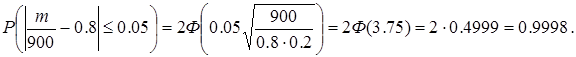
Ответ: 0,9998.
4.7.1. Проверить независимость дискретного случайного вектора, заданного таблицей вероятностей.
| X \ Y | |||
| –3 | 0,05 | 0,1 | 0,05 |
| 0,2 | 0,4 | 0,2 |
Решение. Построим ряды распределения Х и Y.
| Х | -3 | |

| 0,2 | 0,8 |
| Y | |||

| 0,25 | 0,5 | 0,25 |
Проверим теперь выполнение условия  для всех пар индексов i = 1, 2, j = 1, 2, 3. Очевидно, что это условие выполнено для любых i и j. Значит, компоненты X и Y независимы.
для всех пар индексов i = 1, 2, j = 1, 2, 3. Очевидно, что это условие выполнено для любых i и j. Значит, компоненты X и Y независимы.
Ответ: компоненты X и Y независимы.
Контрольная работа
по теме 5 "МАТЕМАТИЧЕСКАЯ СТАТИСТИКА"
5.1.1. Построить гистограмму частот по данным выборки. Найти выборочное среднее, выборочную дисперсию и исправленное выборочное среднее квадратическое отклонение. В качестве вариант взять середины интервалов.
| Интервалы | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 |
| Частоты |
Решение. Гистограмма частот служит для представления интервальных статистических рядов и имеет вид ступенчатой фигуры, состоящей из прямоугольников с основаниями, равными длине h =3 интервалов, и высотами, равными отношению  /h − плотности частоты.
/h − плотности частоты.

Объем выборки

Найдем середины интервалов  :
:

| 2,5 | 5,5 | 8,5 | 11,5 | 14,5 |

|
Выборочная средняя

Выборочная дисперсия



Исправленное среднее квадратическое отклонение

5.2.1. Случайная величина Х имеет нормальное распределение с неизвестным математическим ожиданием М (Х) и дисперсией D (X). По выборке (х 1, х 2,…, хn) объема n = 31 вычислены оценки 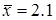 и
и  неизвестных параметров. Найти доверительный интервал для математического ожидания М (Х), отвечающий доверительной вероятности g = 0,8.
неизвестных параметров. Найти доверительный интервал для математического ожидания М (Х), отвечающий доверительной вероятности g = 0,8.
Решение. Доверительный интервал для оценки математического ожидания с надёжностью 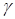 определяют по формуле:
определяют по формуле:

Из соотношения Ф (t) = γ /2 вычисляют значение функции Лапласа:
Ф (t) = 0,4.
По таблице значений функции Лапласа находят t = 1,28. Таким образом,
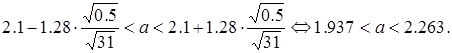
Ответ: 
5.3.1. Применяя метод наименьших квадратов, определить параметры корреляционной зависимости y = a + bx + cx 2 по данным наблюдений, представленных в таблице.
| X | -2 | -1,5 | -1 | -0,5 | 0,5 |
| Y | -1 | -0,2 | 0,8 | 2,5 |
Решение. В соответствии с требованиями метода наименьших квадратов для определения параметров а, b и с необходимо решить следующую систему уравнений:

Составим расчетную таблицу:
| Х | Y | 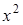
| 
| 
| xy | 
|
| -2 | -1 | -8 | -4 | |||
| -1,5 | 2,25 | -3,375 | 5,0625 | |||
| -1 | -0,2 | -1 | 0,2 | -0,2 | ||
| -0,5 | 0,8 | 0,25 | -0,125 | 0,0625 | -0,4 | 0,2 |
| 0,5 | 2,5 | 0,25 | 0,125 | 0,0625 | 1,25 | 0,625 |
| å = -4,5 | å = 2,1 | å = 7,75 | å = -12,375 | å = 22,1875 | å = 3,05 | å = -3,375 |
Получаем следующую систему уравнений:

Решая ее с помощью пакета программ Excel, находим:

Следовательно, корреляционная зависимость имеет вид:

Ответ: 
5.4.1. Найти выборочный коэффициент линейной корреляции по таблице.
| Х | ||||||||
| Y |
Решение. Рассчитаем выборочный коэффициент линейной корреляции:

Для этого составим расчетную таблицу:
| Х | Y | 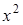
| 
| xy |
| å = 17 | å = 24 | å = 41 | å = 82 | å = 56 |
Получаем:

Ответ: 0,716.
| <== предыдущая лекция | | | следующая лекция ==> |
| Уважаемые консультанты! | | | ЛЕКЦИЯ 81. СССР в 1965-1985 гг. |
Не нашли, что искали? Воспользуйтесь поиском: