Нормальное распределение непрерывной случайной величины. Вероятностный смысл параметров нормального распределения. Нормальная кривая (кривая плотности нормального распределения).

Закон распределения случайной величины называется нормальным (НСВ), если ее плотность распределения задается в виде:

где α и σ- параметры нормального распределения.

Вероятностный смысл параметров нормального распределения:

М_х = α - математическое ожидание,

σ_х = σ - среднее квадратическое отклонение.

График плотности нормального распределения называют нормальной кривой или кривой Гаусса:

Свойства нормального распределения:

1. Зная плотность распределения можно найти функцию распределения:

.

2. Вероятность попадания нормально-распределенной НСВ в интервал (х₁; х₂) определяется по формуле:

,

3.Вероятность того, что отклонение нормально-распределенной НСВ от ее математического ожидания М_х = α по абсолютной величине будет меньше заданного числа ε > 0, определяется по формуле:

.

Интегральная функция Лапласа. Вероятность попадания в заданный интервал нормально распределенной случайной величины. Вероятность отклонения нормально распределенной случайной величины от своего математического ожидания. Правило трех сигм.

Интегральная теорема Лапласа: Если вероятность удачи p в одном из n независимых испытаний с двумя исходами постоянна и отлична от нуля и единицы, то вероятность появления от k1 до k2 удач приближенно равна:

,

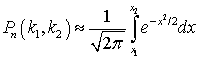где , .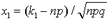

Вероятность того, что Х примет значение, принадлежащее интервалу (α,β)

P(α<X<β)=Ф((β-a)/σ)-Ф((α-a)/σ),

Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения (правило 3 сумм).

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:

Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:

Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.

Не нашли, что искали? Воспользуйтесь поиском: