Комбинированный метод

Комбинируя метод секущих и метод Ньютона, получается нестационарный метод отыскания действительных корней уравнения (7.1). Преимущество получаемого метода заключается в том, что при прежних предположениях относительно последовательные приближения и лежат по разные стороны от корня, и поэтому можно следить в процессе вычислений за достигнутой точностью. В то же время он сходится значительно быстрее метода секущих.

Пусть на отрезке содержится единственный корень уравнения (7.1), а на этом отрезке не меняют знаков.

Если , то находим и по формулам:

, (7.19)

а следующие приближения находятся по формулам:

. (7.20)

Если , то находим и по формулам:

, (7.21)

а следующие приближения находятся по формулам (20).

Геометрическая интерпретации комбинированного метода выглядит следующим образом:

Рис. 14 Комбинированный метод

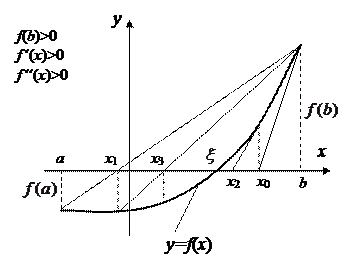
Рис. 15 Комбинированный метод

Рис. 16 Комбинированный метод

Рис. 17 Комбинированный метод

Пример. Методом хорд и Ньютона с точностью решить уравнение

.

Решение. Определим по правилу Декарта число положительных и отрицательных корней. Пусть . Имеем два положительных коэффициента (1 и 3) и один отрицательный (-3) коэффициент. Но тогда уравнение имеет, по крайней мере, один положительный корень, т.к. имеется только одна перемена знака. Теперь, заменяя на , получим, что в коэффициентах уравнения имеется две перемены знака, а это означает, что данное уравнение имеет два отрицательных действительных корня.

Отделение корней проведем аналитически. Функция определена для любых . Найдем производные, а затем критические точки:

, , , и .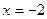

Составим таблицу знаков для функции :

х		-3	-2			+1
Sign f(x)	–	–	+	–	–	+	+

Имеется три перемены знака, следовательно, действительные корни лежат в интервалах: (-3,-2), (-2,1) и (0,1).

Теперь перейдем непосредственно к вычислению корней. При вычислениях будем использовать видоизменение метода Ньютона (18) с постоянным значением производной:

(7.22)

Для окончания счета по методу хорд или методу Ньютона воспользуемся зависимостью

.

Но для этого сначала надо проверить, что для выбранного интервала выполняется условие , где , .

Возьмем сначала промежуток 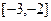. Имеем

, .

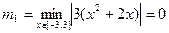Значит, .

Разделим данный промежуток на две части и рассмотрим отрезки и . На первом промежутке функция меняет знак (значит здесь лежит корень уравнения), а на втором – нет. Тогда для первого промежутка и . Опять имеем . Снова разбиваем интервал на две части и после проверки знаков функции остается промежуток , на котором и , но тогда .

Теперь уточним корень, лежащий на отрезке по:

– методу хорд(секущих) по формулам (7.12)

и ,

где .

Проделав вычисления, получим, что .

– методу Ньютона (касательных), применяя формулу (7.22), учитывая, что и , получим .

Результаты вычислений по обоим методам приведены в таблице.

Таблица вычислений

Метод хорд		Метод Ньютона
	-2.5	-0.02532			-2.75
	-2.52532	-0.00537			-2.57071	0.17929
	-2.53069	-0.00111			-2.54436	0.02634
	-2.5318	-0.00023			-2.53623	0.00813
					-2.53351	0.00272
					-2.53258	0.00093

Для метода хорд , а для метода Ньютона, так как , то .

Не нашли, что искали? Воспользуйтесь поиском: