Определение топологического пространства

Определение. Покрытием множества A называется такое семейство множеств {U_a}, что объединение элементов этого семейства содержит множество A: .

Замечание. В общем случае элементы покрытия могут как содержаться в покрываемом множестве, так и содержать элементы, не принадлежащие ему.

Примеры:

1. Черепица на крыше является покрытием крыши, если она не течет.

2. Если A= R, то следующие семейства являются его покрытиями:

а) {U_a}={(n-1;n+1), nÎZ};

б) {U_a}={ [ n-1;n ], nÎZ};

в) {U_a} – множество всех открытых интервалов. Забегая вперед, скажем, что это покрытие образует топологию числовой прямой, которая называется естественной.

3. Множество кругов на плоскости является покрытием плоскости, а также любой фигуры, лежащей в этой плоскости.

Определение. Подпокрытием покрытия {U_a} множества A называется такое подсемейство {U_b}Ì{U_a}, которое само является покрытием множества A.

Примеры. 1. В случае примеров 1, 2а, 2б подпокрытий нет.

2. Если из множества всех открытых интервалов (пример 2в) выделить, например, семейство 2а, то это будет подпокрытие.

3. Семейство {U_b} = {{a,b,m}, {b,c,m}, {c,d,m}, {a,k,m}} является покрытием множества A={a,b,c,d,k}, причем элементы покрытия не содержатся в A; покрытие {U_b} подпокрытий не содержит.

Определение. Топологией t на множестве X называется такое покрытие этого множества, элементы которого являются подмножествами X и удовлетворяют следующим аксиомам:

1) ÆÎ t (пустое множество является элементом из t);

2) X Î t (множество X - элемент из t);

3) 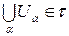(объединение любого числа элементов из t - элемент из t);

4) (пересечение конечного числа элементов из t - элемент из t).

Определение. Топологическим пространством называется пара (X, t), где X – непустое множество с некоторой топологией t.

Определение. Элементы любой топологии называются открытыми множествами этой топологии, а элементы пространства X называются точками топологии.

С учетом данного определения аксиомы топологического пространства могут быть сформулированы следующим образом:

1) Æ открыто;

2) множество X открыто;

3) объединение любого числа открытых множеств открыто;

4) пересечение конечного числа открытых множеств открыто.

Примеры: 1. На любом множестве X≠ Æ всегда существует топология, называемая тривиальной или антидискретной, состоящая из самого множества X и Æ. Антидискретная топология является минимальной топологией на X.

2. В пространстве Rⁿ множество открытых параллелепипедов задает топологическое пространство с естественной топологией.

Определение. Множество A называется замкнутым в топологическом пространстве (X, t), если его дополнение C_XA до множества X открыто в топологии этого пространства.

Замечание. Достаточно очевидно, что произвольное множество в топологическом пространстве может быть открытым, замкнутым, открыто-замкнутым и не открытым и не замкнутым. В частности, множества Æ и t являются открыто-замкнутыми в любой топологии и в силу этого называются тривиальными открыто-замкнутыми множествами.

Пример. Пусть X - произвольное непустое множество, а t - множество всех подмножеств множества X. Тогда t - топология на X. Эта топология называется дискретной. Она является максимальной топологией на X. Характерным для дискретной топологии является то, что в этой топологии любое подмножество открыто - замкнуто.

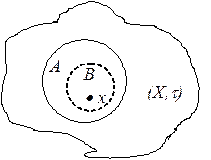§2 Взаимное расположение точек и множеств