
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Временное и стационарное уравнение Шредингера.
Состояние частицы в квантовой механике определяется заданием волновой функции 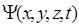 , зависящей от координат и времени. Следовательно, для отыскания явного вида волновой функции в квантовой механике необходимо иметь уравнение, подобное уравнению движения Ньютона в классической механике. Такое уравнение было найдено Э. Шредингером в 1926 году. Уравнение Шредингера не выводится, а постулируется на основе известных опытных фактов, и справедливость его доказывается согласием теоретических расчетов и опытных данных. В общем случае уравнение Шредингера имеет вид
, зависящей от координат и времени. Следовательно, для отыскания явного вида волновой функции в квантовой механике необходимо иметь уравнение, подобное уравнению движения Ньютона в классической механике. Такое уравнение было найдено Э. Шредингером в 1926 году. Уравнение Шредингера не выводится, а постулируется на основе известных опытных фактов, и справедливость его доказывается согласием теоретических расчетов и опытных данных. В общем случае уравнение Шредингера имеет вид
 , (14.6)
, (14.6)
где  – масса частицы,
– масса частицы,  Дж×с – постоянная Планка,
Дж×с – постоянная Планка,  – мнимая единица,
– мнимая единица,  – волновая функция,
– волновая функция,  – потенциальная энергия частицы в силовом поле, в котором движется частица,
– потенциальная энергия частицы в силовом поле, в котором движется частица,  – оператор Лапласа, показывающий, какую операцию нужно провести над волновой функцией
– оператор Лапласа, показывающий, какую операцию нужно провести над волновой функцией 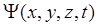 . Уравнение (14.7) справедливо для любой частицы, движущейся со скоростью
. Уравнение (14.7) справедливо для любой частицы, движущейся со скоростью  (с – скорость света в вакууме). Уравнение Шредингера накладывает дополнительные условия на волновую функцию
(с – скорость света в вакууме). Уравнение Шредингера накладывает дополнительные условия на волновую функцию 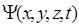 :
:
1) волновая функция  должна быть конечной, непрерывной и однозначной;
должна быть конечной, непрерывной и однозначной;
2) волновая функция 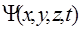 должна иметь непрерывные частные производные
должна иметь непрерывные частные производные  ;
;
3) функция 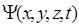 должна быть интегрируема, т.е. интеграл
должна быть интегрируема, т.е. интеграл  должен быть конечным.
должен быть конечным.
Для стационарных состояний одномерное уравнение Шредингера имеет вид
 , (14.7)
, (14.7)
где 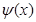 – волновая функция, описывающая состояние частицы,
– волновая функция, описывающая состояние частицы,  – масса частицы, Е – полная энергия,
– масса частицы, Е – полная энергия,  – потенциальная энергия частицы.
– потенциальная энергия частицы.
Из решения уравнения Шредингера (14.7) для движения электрона в случае одномерного, бесконечно глубокого, прямоугольного потенциального ящика следует, что собственная нормированная волновая функция равна

 (14.8)
(14.8)
и собственное значение энергии равно
 , (14.9)
, (14.9)
где  – ширина потенциального ящика,
– ширина потенциального ящика,  = 1,2,3…
= 1,2,3…
В области  .
.
В случае потенциального барьера U(x) произвольной формы формула коэффициента прозрачности D имеет вид
 (14.10)
(14.10)
где x 1 и x 2 – координаты точек, между которыми  > E.
> E.
Прохождение частицы сквозь потенциальный барьер называется туннельным эффектом.
84. Частица в одномерной прямоугольной яме (потенциальном ящике).
Для свободной частицы  (она движется вдоль оси х) решением уравнения Шредингера
(она движется вдоль оси х) решением уравнения Шредингера
 (14.3)
(14.3)
будет функция
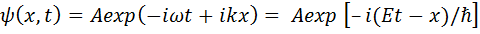 , (14.4)
, (14.4)
где 

 волновое число – может принимать любые положительные значения,
волновое число – может принимать любые положительные значения,  - непрерывный спектр энергий.
- непрерывный спектр энергий.
Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует независящая от времени плотность вероятности обнаружения частицы в точке пространства  , т.е. все положения свободной частицы в пространстве являются равновероятными пространстве.
, т.е. все положения свободной частицы в пространстве являются равновероятными пространстве.
Частица находится в одномерной прямоугольной яме шириной  Рисунок 14.1
Рисунок 14.1

| Уравнение Шредингера для стационарных состояний в пределах ямы:
 (14.5)
Граничным условиям удовлетворяет решение (14.5)
Граничным условиям удовлетворяет решение
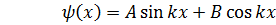 , (14.6) , (14.6)
   . .
|
| Рис. 14.1. Потенциальная яма |
 (n=1, 2, 3 …) (14.7)
(n=1, 2, 3 …) (14.7)
- собственные значения  . При этом минимально возможное значение энергии
. При этом минимально возможное значение энергии  .
.
Т.о. энергия частицы в бесконечно высокой потенциальной яме принимает лишь определенные дискретные значения, т.е. квантуется. Квантовые значения энергии  называются уровнями энергии, а число n, определяющее энергетические уровни частицы называется главным квантовым числом.
называются уровнями энергии, а число n, определяющее энергетические уровни частицы называется главным квантовым числом.
Cобственные волновые функции  , (14.8)
, (14.8)
с учетом нормировки  (14.9)
(14.9)
будут иметь вид:
 (n=1, 2, 3 …) (14.10)
(n=1, 2, 3 …) (14.10)
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
а) 
 (собственная нормированная волновая функция);
(собственная нормированная волновая функция);
б)  (собственное значения энергии),
(собственное значения энергии),
где  - квантовое число (
- квантовое число ( =1,2,3,…);
=1,2,3,…);  - ширина ящика. В области
- ширина ящика. В области 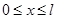
 и
и 
85.
Уравнение Шредингера для атома водорода
Стационарное уравнение Шредингера для электрона в атоме водорода с учетом (14.12) имеет вид:
 . (14.13)
. (14.13)
Масса ядра больше массы электрона, поэтому рассматривается движение электрона относительно неподвижного ядра. Т.к. движение электрона происходит в сферически симметричном центральном поле, то, используя сферическую систему координат (r, θ, φ) получим:
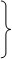
 .
.
Уравнение Шредингера в сферических координатах примет вид:
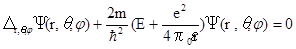 . (14.14)
. (14.14)
Решение уравнения (14.14) выходит за рамки общего курса физики.
Из решения уравнения (14.14) следует, что момент импульса электрона в атоме водорода имеет дискретные значения (квантуется):
 , (14.15)
, (14.15)
где l = 0, 1, 2, …, (n-1) - орбитальное квантовое число. Полная энергия электрона в атоме Е < 0 и принимает дискретные значения (квантуется):
 , (14.16)
, (14.16)
где nr - радиальное квантовое число.
Сравним (14.16) с полной энергией электрона в атоме водорода по Бору:
 .
.
Получим n = nr + l + 1, (14.17)
где n = 1, 2, 3,.... - главное квантовое число.
14.4.2 Энергетические уровни
Энергетические уровни электрона в атоме водорода зависят только от главного квантового числа n. Из (14.17) следует, что наибольшему значению l при заданном n соответствует nr=0, т.е. lmax= n–1. Следовательно, при заданном значении n орбитальное квантовое число l принимает следующие значения:
l = 0, 1, 2, …, (n-1). (14.18)
Состояния электрона с различными значениями орбитального квантового числа, обозначают следующим образом: l = 0 (S – состояние), l = 1 (p – состояние), l = 2 (d- состояние) и т.д. в соответствии c латинским алфавитом.
Рассмотрим основное состояние электрона в атоме водорода, когда n = 1 и l = 0 (S - состояние). S - состояние электрона сферически симметрично, т.е. волновая функция зависит от r. Уравнение Шредингера для S - состояния:
 . (14.19)
. (14.19)
Решение уравнения имеет вид:
 , (14.20)
, (14.20)
где с и а0 – постоянные величины. Величина Е1 в (14.19) - энергия основного состояния электрона. Подставим первую и вторую производные от функции (14.20) в уравнение (14.19) после преобразований получим
 . (14.21)
. (14.21)
Левая часть равенства (12.10)не зависит от r, поэтому для выполнения равенства необходимо, чтобы левая и правая части равенства были равны 0:

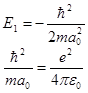 . (14.22)
. (14.22)
Из второго уравнения (14.22) следует, что
 . (14.24)
. (14.24)
Из (14.24) видно, что выражение для а0 совпадает с выражением для радиуса r1 первой боровской орбиты. Из первого уравнения (14.22) получим выражение для энергии основного состояния n = 1 атома водорода
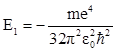 . (14.23)
. (14.23)
Вероятность обнаружить электрон в шаровом слое с объемом dV = 4πr2dr на расстоянии от r до r+dr от ядра будет равна
 . (14.24)
. (14.24)
Подставляя в последнее выражение волновую функцию (14.19) получим:
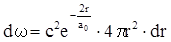 (14.25)
(14.25)
Максимальную вероятность нахождения электрона на расстоянии rmax от ядра, найдем, приравняв производную dω/dr от функции  нулю. dω/dr = 0, при r max= а0. Отсюда следует, что боровские орбиты являются не классическими траекториями, а геометрическими местами точек, где вероятность обнаружить электрон– максимальна (рисунок 12.1). Модуль вектора момента импульса принимает дискретные значения кратные l, формула (14.18). Какова ориентация вектора момента импульса электрона в пространстве?
нулю. dω/dr = 0, при r max= а0. Отсюда следует, что боровские орбиты являются не классическими траекториями, а геометрическими местами точек, где вероятность обнаружить электрон– максимальна (рисунок 12.1). Модуль вектора момента импульса принимает дискретные значения кратные l, формула (14.18). Какова ориентация вектора момента импульса электрона в пространстве?
Орбитальный момент импульса электрона в атоме и соответствующий орбитальный магнитный момент связаны соотношением:

|  . (14.26) где ge = e/2me - орбитальное гиромагнитное отношение. Направления векторов . (14.26) где ge = e/2me - орбитальное гиромагнитное отношение. Направления векторов  и и  в пространстве связаны с направлением внешнего магнитного поля. В теории Бора вектор орбитального момента импульса в пространстве связаны с направлением внешнего магнитного поля. В теории Бора вектор орбитального момента импульса  и вектор орбитального магнитного момента по отношению к направлению внешнего магнитного поля ориентированы произвольным образом. В квантовой механике показано, что вектор момента импульса электрона может принимать строго определенные ориентации в пространстве, и вектор орбитального магнитного момента по отношению к направлению внешнего магнитного поля ориентированы произвольным образом. В квантовой механике показано, что вектор момента импульса электрона может принимать строго определенные ориентации в пространстве,
|
| Рисунок 14.3 Наибольшая вероятность нахождения электрона |
при которых проекция вектора 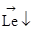 на направление Z внешнего магнитного полякратна ћ, т.е. квантована. Это утверждение называют правилом пространственного квантования - следствие обобщенного правила А. Зоммерфельда для квантования боровских орбит.
на направление Z внешнего магнитного полякратна ћ, т.е. квантована. Это утверждение называют правилом пространственного квантования - следствие обобщенного правила А. Зоммерфельда для квантования боровских орбит.
Таким образом:
 , (14.27)
, (14.27)
где m= 0, ±1, ±2, …, ± l – магнитное квантовое число. Из (12.17) следует, что вектор 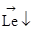 может принимать 2 l +1 ориентации в пространстве
может принимать 2 l +1 ориентации в пространстве
относительно внешнего магнитного поля. Возможные ориентации вектора 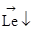 в пространстве для электронов в р - и d – состояниях показан на рисунке 14.4
в пространстве для электронов в р - и d – состояниях показан на рисунке 14.4

|
 Рисунок 14.5Схема опытов Штерна-
Герлаха
Рисунок 14.5Схема опытов Штерна-
Герлаха
|
Рисунок 14.4 Ориентации вектора 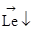
|
Наличие пространственного квантования подтвердили опыты О.Штерна и В. Герлаха в 1921г. В опытах (рисунок 14.5) нагретый до высокой температуры серебряный шарик К испускал атомы серебра со средней тепловой скоростью около 100м/с. Диафрагма В выделяет узкий пучок атомов, который далее проходит через сильное и неоднородное магнитное поле с градиентом индукции  , направленным перпендикулярно пучку. Для исключения
, направленным перпендикулярно пучку. Для исключения
рассеяния атомов серебра на атомах воздуха, система помещалась в вакуум порядка 10-5мм.рт.ст. После прохождения магнитного поля атомы серебра попадают на фотопластинку А. Для произвольных ориентаций 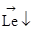 относительно направления магнитного поля в центре фотопластинки должна наблюдаться сплошная темная линия с уменьшением плотности к краям полосы. Опыты с различными металлами давали на фотопластинке две резкие полосы. Атомы отклоняются в магнитном поле в двух направлениях(двух возможных ориентациях вектора магнитного момента во внешнем магнитном поле). На каждый атом в магнитном поле действует сила:
относительно направления магнитного поля в центре фотопластинки должна наблюдаться сплошная темная линия с уменьшением плотности к краям полосы. Опыты с различными металлами давали на фотопластинке две резкие полосы. Атомы отклоняются в магнитном поле в двух направлениях(двух возможных ориентациях вектора магнитного момента во внешнем магнитном поле). На каждый атом в магнитном поле действует сила:
 . (14.28)
. (14.28)
Из выражений (12.4) и (12.16) следует
 , (14.29)
, (14.29)
где  Дж/Тл - магнетон Бора.
Дж/Тл - магнетон Бора.
86. Принцип Паули
Т.о., состояние электрона в атоме определяют четыре квантовых числа: главное квантовое число n, орбитальное квантовое число l, магнитное квантовым число m, спиновое квантовое число mS. Используя квантово - механическое положение о неразличимости тождественных частиц, В. Паули установил принцип: в любом атоме не может быть двух электронов в стационарных состояниях, определяемых одинаковым набором квантовых чисел:  . Число электронов
. Число электронов 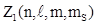 , с одинаковым набором четырех квантовых чисел:
, с одинаковым набором четырех квантовых чисел:  = 0 или 1.Число электронов с одинаковым набором трех чисел
= 0 или 1.Число электронов с одинаковым набором трех чисел  = 2 т.к. mS принимает два значения +1/2 и -1/2. Максимальное число электронов в состояниях с двумя одинаковыми квантовыми числами n и l:
= 2 т.к. mS принимает два значения +1/2 и -1/2. Максимальное число электронов в состояниях с двумя одинаковыми квантовыми числами n и l:
 .
.
Суммируя последнее равенство от l =0 до l = n-1, найдем число электронов в состояниях, определяемых главным квантовым числом n:
 . (14.32)
. (14.32)
Максимальное число электронов в состояниях с главным n и орбитальным l – квантовыми числами.
Таблица 1
| Оболочка | Количество электронов в состояниях | Мах число электронов | |||||

|  
| 
| 
| ||||
| К | - | - | - | - | |||
| L | - | - | - | ||||
| М | - | - | |||||
| N | - | ||||||
| Р |
В таблице показано максимальное число электронов в состояниях, характеризуемых значениями главного n и орбитального l квантовых чисел.
Для атома гелия, имеющего два электрона, решение уравнения Шредингера усложняется. Решение задачи возможно для элементов первой группы таблицы Менделеева - щелочных металлов, с заполненными внутренними оболочками и одним электроном на внешней оболочке. Движение электрона рассматривают в поле, создаваемом общим зарядом ядра 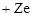 и зарядом
и зарядом 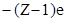 заполненных электронных оболочек. Тогда общий заряд ядра и заполненных оболочек равен заряду одного протона +е.
заполненных электронных оболочек. Тогда общий заряд ядра и заполненных оболочек равен заряду одного протона +е.
87. Строение атомных ядер. Модели ядра
Опыты Резерфорда по наблюдению рассеяния  - частиц показали, что атом имеет ажурное строение - большая часть пространства атома (радиус атома около 10-10 м) не занята веществом. В центре атома находится ядро (радиус ядра 10-15 ÷ 10-14м), в котором сосредоточена основная масса и весь положительный заряд атома. Вокруг ядра по замкнутым орбитам движутся отдельные электроны. Заряд атомного ядра является одной из важнейших его характеристик. Оказалось, что величина заряда ядра атома любого элемента равна произведению заряда электрона
- частиц показали, что атом имеет ажурное строение - большая часть пространства атома (радиус атома около 10-10 м) не занята веществом. В центре атома находится ядро (радиус ядра 10-15 ÷ 10-14м), в котором сосредоточена основная масса и весь положительный заряд атома. Вокруг ядра по замкнутым орбитам движутся отдельные электроны. Заряд атомного ядра является одной из важнейших его характеристик. Оказалось, что величина заряда ядра атома любого элемента равна произведению заряда электрона  на порядковый номер элемента в таблице Менделеева
на порядковый номер элемента в таблице Менделеева 
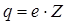 (15.1)
(15.1)
Д.Д. Иваненко и В. Гейзенберг независимо разработали протоно - нейтронную модель атомных ядер. В этой модели ядро любого атома состоит из протонов р и нейтронов n. Протон р - положительно заряженная элементарная частица, заряд которой численно равен заряду электрона ( Кл), масса покоя протона mp=1,6726×10-27кг» 1836me, где me - масса покоя электрона. Нейтрон n – нейтральная элементарная частица, масса покоя которой
Кл), масса покоя протона mp=1,6726×10-27кг» 1836me, где me - масса покоя электрона. Нейтрон n – нейтральная элементарная частица, масса покоя которой  кг» 1839 me, т.е. близка к массе покоя протона. Протоны и нейтроны называют нуклонами, т.е. ядерными частицами, чтобы отличить от других элементарных частиц.
кг» 1839 me, т.е. близка к массе покоя протона. Протоны и нейтроны называют нуклонами, т.е. ядерными частицами, чтобы отличить от других элементарных частиц.
В свободном состоянии нейтрон не стабилен. (радиоактивен). Самопроизвольно распадается, превращаясь в протон и испускает электрон. И еще идну частицу – нейтрино. Период полураспада равен приблизительно 12 мин. Схема распада
 .
.
Общее число нуклонов в ядре называют массовым числом А. Если число протонов в ядре Z, а нейтронов - N, то массовое число.
А = Z + N.
Число протонов Z называют зарядовым числом. Оно совпадает с порядковым номером химического элемента в Периодической системе элементов Менделеева. Число электронов в атоме равно числу протонов в ядре. Известны 107 элементов, их зарядовые числа от Z=1 до Z=107.
Символически ядро обозначают так:  , где Х - символ химического элемента. Ядра всех атомов данного химического элемента имеют одинаковый положительный заряд, следовательно, они содержат одно и то же число протонов Z. Число нейтронов N = A-Z, в атомных ядрах одного и того же элемента, могут быть различными.
, где Х - символ химического элемента. Ядра всех атомов данного химического элемента имеют одинаковый положительный заряд, следовательно, они содержат одно и то же число протонов Z. Число нейтронов N = A-Z, в атомных ядрах одного и того же элемента, могут быть различными.
Изотопы - атомные ядра с одинаковым Z, но различным числом N.
Изотопы одного и того же элемента имеют одинаковые химические характеристики, но различные массы. У водорода три изотопа: протий -  ; дейтерий -
; дейтерий -  ; тритий-
; тритий-  . У изотопов урана
. У изотопов урана  одинаковое число протонов, равное 92, а число нейтронов различно.
одинаковое число протонов, равное 92, а число нейтронов различно.
Изобары - ядра с одинаковым числом нуклонов А, но с различным числом протонов. Примеры изобар -  .
.
Ядра и элементарные частицы имеют еще одну характеристику - спин (spin- с англ. – «вращать»). Спин - собственный момент импульса частицы. Величина спина не зависит от состояния движения частицы. Спин частицы, согласно квантовой теории, равен целому (0,1,2,¼) или полуцелому  числу постоянных Планка
числу постоянных Планка  . Протоны, нейтроны, электроны имеют полуцелый спин
. Протоны, нейтроны, электроны имеют полуцелый спин  – класс частиц, называемый фермионы. Бозоны, имеют целый спин.
– класс частиц, называемый фермионы. Бозоны, имеют целый спин.
Радиус и плотность ядра
Форма атомных ядер близка к сферической форме. Радиус ядра определяется эмпирической формулой
 , (15.2)
, (15.2)
где  м, А - число нуклонов.
м, А - число нуклонов.
Из (15.2) следует, что объем ядра пропорционален числу нуклонов. Следовательно, все ядра, независимо от размеров имеют одинаковую плотность:
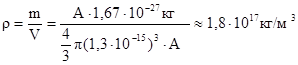 .
.
Плотность ядра – очень большая величина. Шар радиусом 200м и данной плотностью вещества имел бы массу, равную массе земного шара.
Модели ядра
Рассмотрим капельную и оболочечную модели ядра. Капельная модель предложена в 1936г. Н. Бором и Я.И. Френкелем. Согласно модели ядро – сферическая капля из заряженной несжимаемой сверхплотной ядерной жидкости.
Капельная модель основана на аналогии между поведением молекул в капле жидкости и поведением нуклонов в ядре. Силы, действующие между молекулами и нуклонами в ядре, короткодействующие, им свойственно насыщение. Капля жидкости при неизменных внешних условиях имеет постоянную плотность. Ядра имеют постоянную плотность, не зависящую от числа нуклонов в ядре. Объемы ядра и капли жидкости пропорциональны числу частиц. Капельная модель ядра - электрически заряженная капля несжимаемой жидкости, подчиняется законам квантовой механики. Модель объяснила механизм ядерных реакций, реакцию деления ядер.
Оболочечная модель предложена М. Тапперт - Майер и Х. Йенсен в 1950г. В модели нуклоны заполняют дискретные энергетические уровни (оболочки), согласно принципу Паули. Устойчивость ядер в модели связана с характером заполнения уровней. Наиболее устойчивыми ядрами являются ядра, с полностью заполненными оболочками. Существуют особо устойчивые (магические) ядра. Оболочечная модель объяснила магнитные моменты, спины и различную устойчивость ядер, периодичность изменения их свойств.
Оболочная модель описывает легкие и средние ядра и ядра в невозбужденном (основном) состоянии.
88.
Не нашли, что искали? Воспользуйтесь поиском: