Выбор независимых переменных 8 страница

Таблица 5.3

Результаты оптимизации тестовой функции

методом параллельных касательных

Оптимизируемая функция	Число шагов	Независимые переменные
	J
–
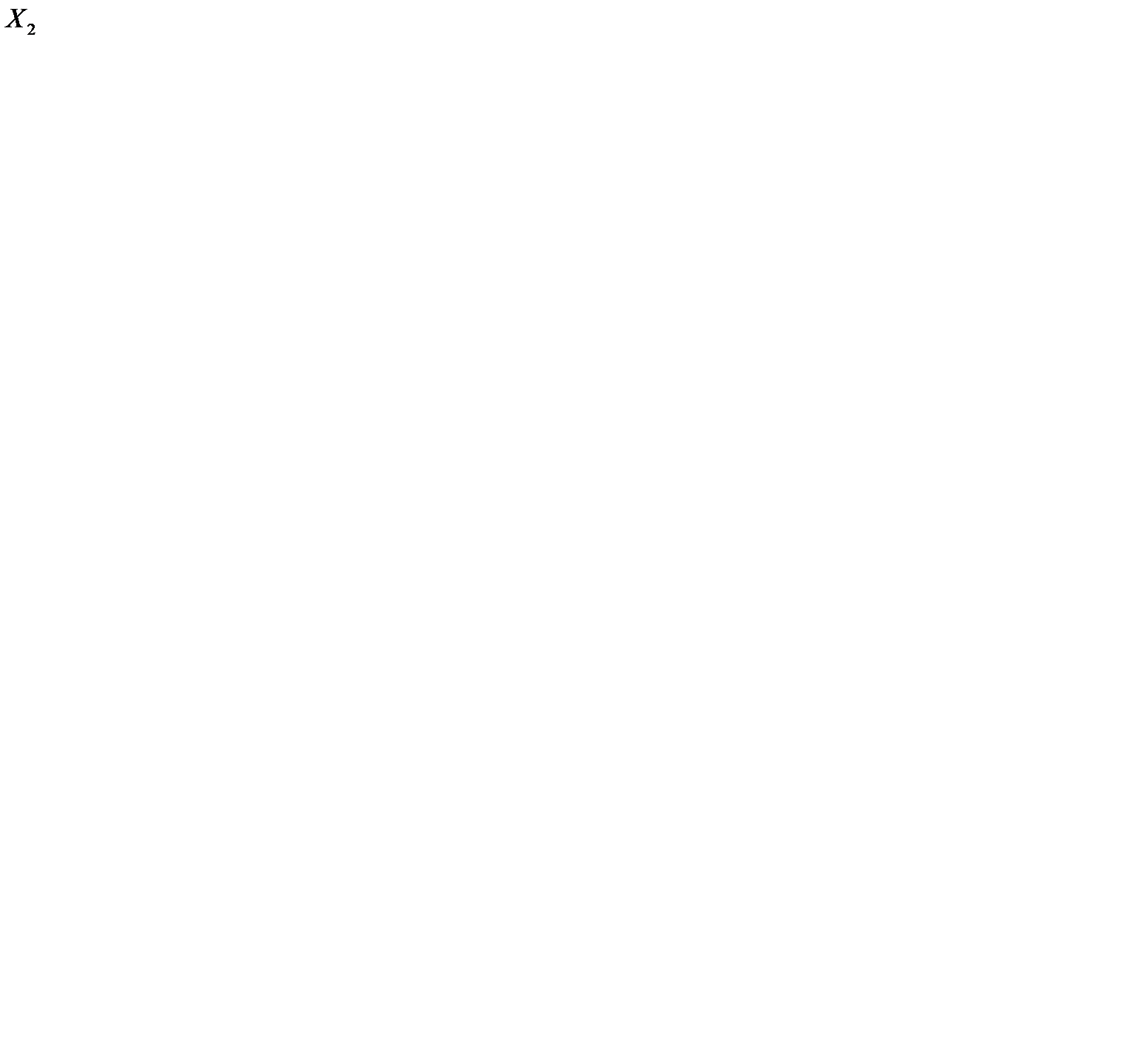
1486,3		13,7	14,6	15,5	16,4	17,25	18,12	18,99	19,86	20,73	21,6
19,75		2,47	3,46	4,44	5,436	6,411	7,395	8,381	9,366	10,351	11,337
0,0151		1,04	2,039	3,049	4,038	5,038	6,037	7,037	8,037	9,036	10,036
		0,997	1,997	2,997	4,007	4,997	5,997	6,997	7,997	8,997	9,997
		0,999	1,999	2,999	3,999	4,999	5,999	6,999	7,999	9,000	10,000

Таблица 5.4

Результаты оптимизации тестовой функции

методом наискорейшего спуска

Оптимизируемая функция	Число шагов	Независимые переменные
	J
–
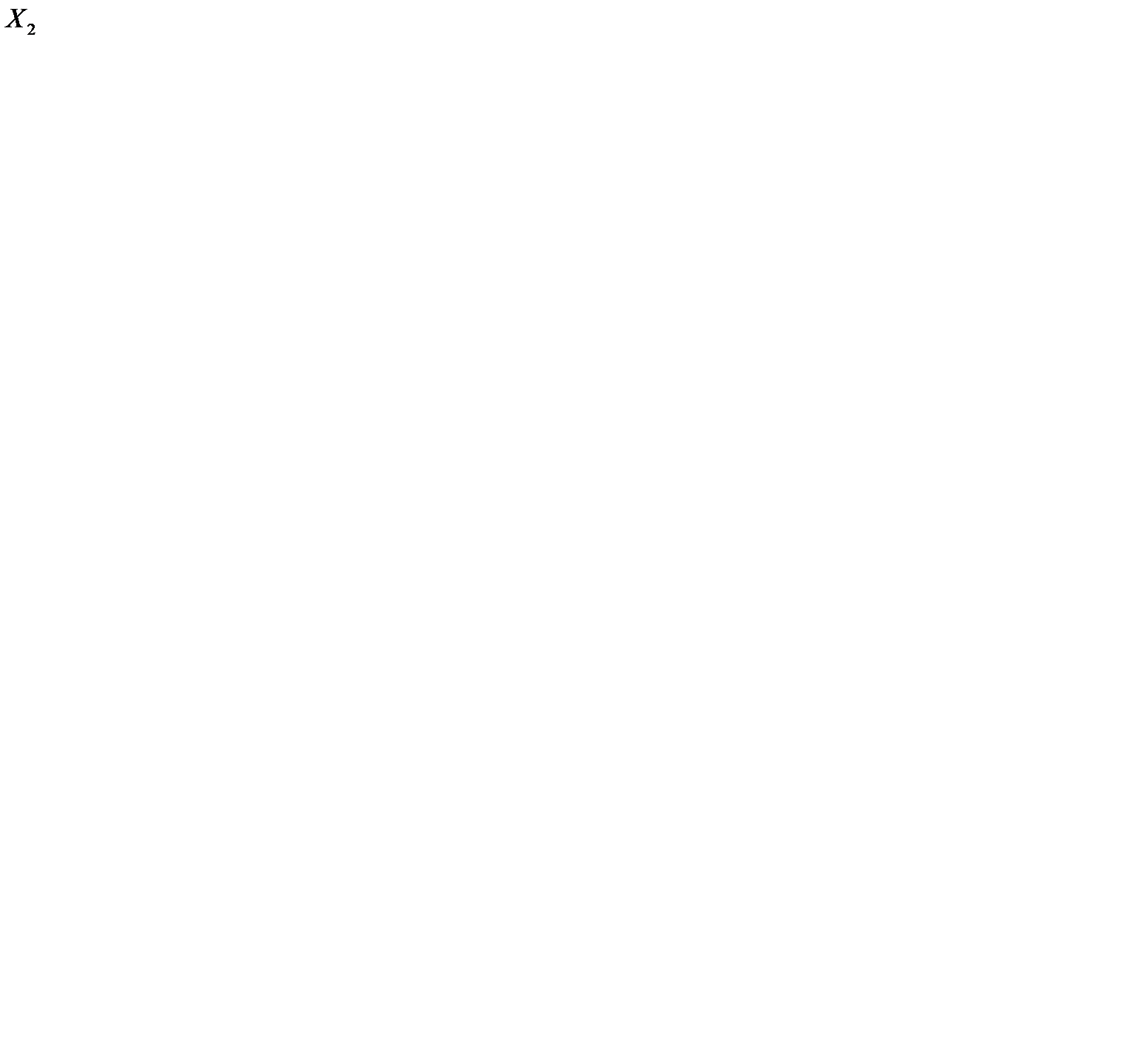
186,5		5,52	6,47	7,43	8,38	9,34	10,29	11,24	12,2	13,2	14,1
0,0256		1,05	2,05	3,06	4,05	5,05	6,06	7,05	8,,05	9,05	10,05
		1,001	2,001	3,001	4,001	5,001	6,001	7,000	8,000	9,000	10,000

Таблица 5.5

Результаты оптимизации тестовой функции

методом Гаусса – Зейделя

Оптимизируемая функция	Число шагов	Независимые переменные
	J
–
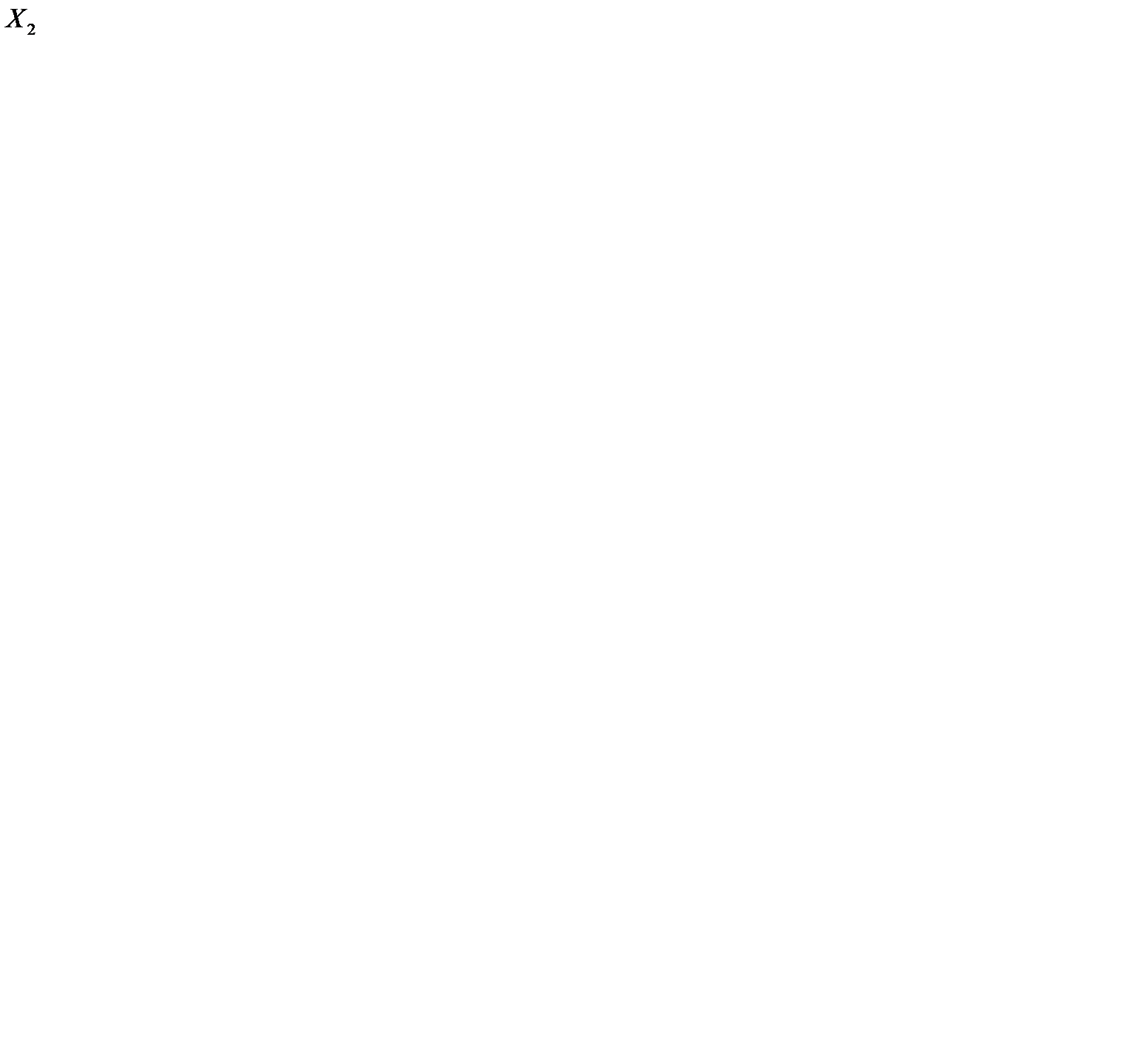
		15,74	18,56	14,84	82,55
		15,74	18,56	14,84	11,67	9,49	8,88	10,6	15,45	5,042
68,1		1,288	1,076	-4,98	2,43	5,06	6,687	6,386	8,248	9,026	9,73
0,275		0,785	1,99	2,772	3,6	5,014	6,1	6,92	8,08	9,008	9,998
0,00316		1,015	1,998	2,997	3,997	5,013	5,965	6,953	8,009	9,005	10,001
0,000044		1,003	1,998	2,997	3,996	5,001	5,997	7,000	8,002	9,002	10,001

Таблица 5.6

Результаты оптимизации тестовой функции

методом конфигураций

Оптимизируемая функция	Число шагов	Независимые переменные
	J
–
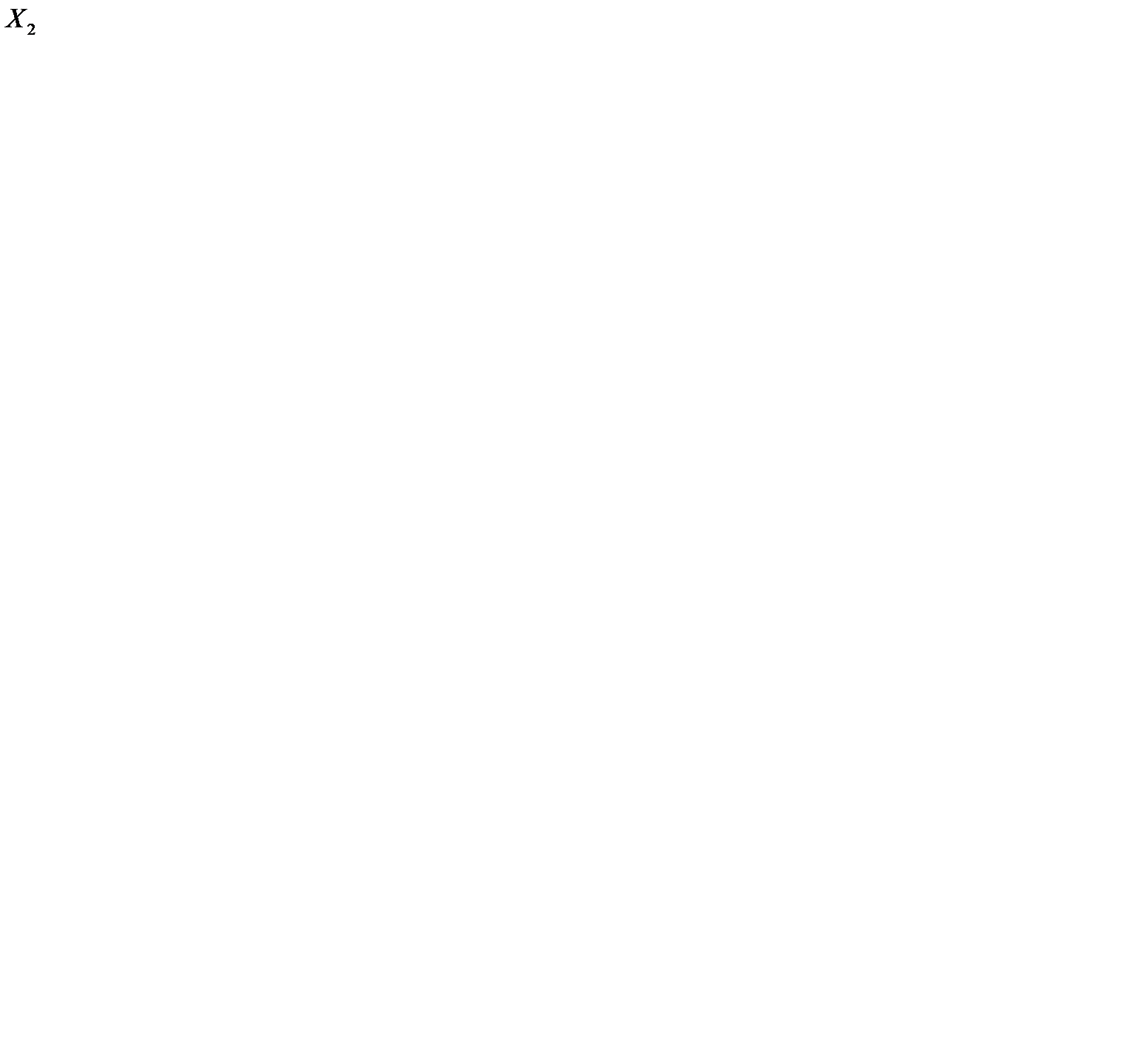
		96,5	96,5	96,5	96,5	97,1	97,1	97,1	97,1	97,1	97,1
		90,5	90,5	90,5	90,5	90,5	90,5	90,5	90,5	92,4	92,4
		71,68	71,68	75,64	73,66	73,66	73,66	73,66	73,66	73,66	73,66
		46,86	46,86	46,86	46,86	46,86	46,86	46,86	50,27	50,27	50,27
21,68		1,879	3,817	3,814	3,814	3,814	3,814	9,697	9,697	9,697	9,697
0,36		1,274	1,988	3,27	3,912	5,145	6,112	7,35	8,000	9,194	10,1
0,00484		0,999	2,01	2,993	4,01	4,993	5,991	7,056	8,000	8,993	9,999
0,00175		0,999	2,01	2,992	4,01	4,993	5,991	78,036	8,000	8,993	9,999

Таблица 5.7

Результаты оптимизации тестовой функции

методом квадратичной аппроксимации

Оптимизируемая функция	Число шагов	Независимые переменные
	J
–
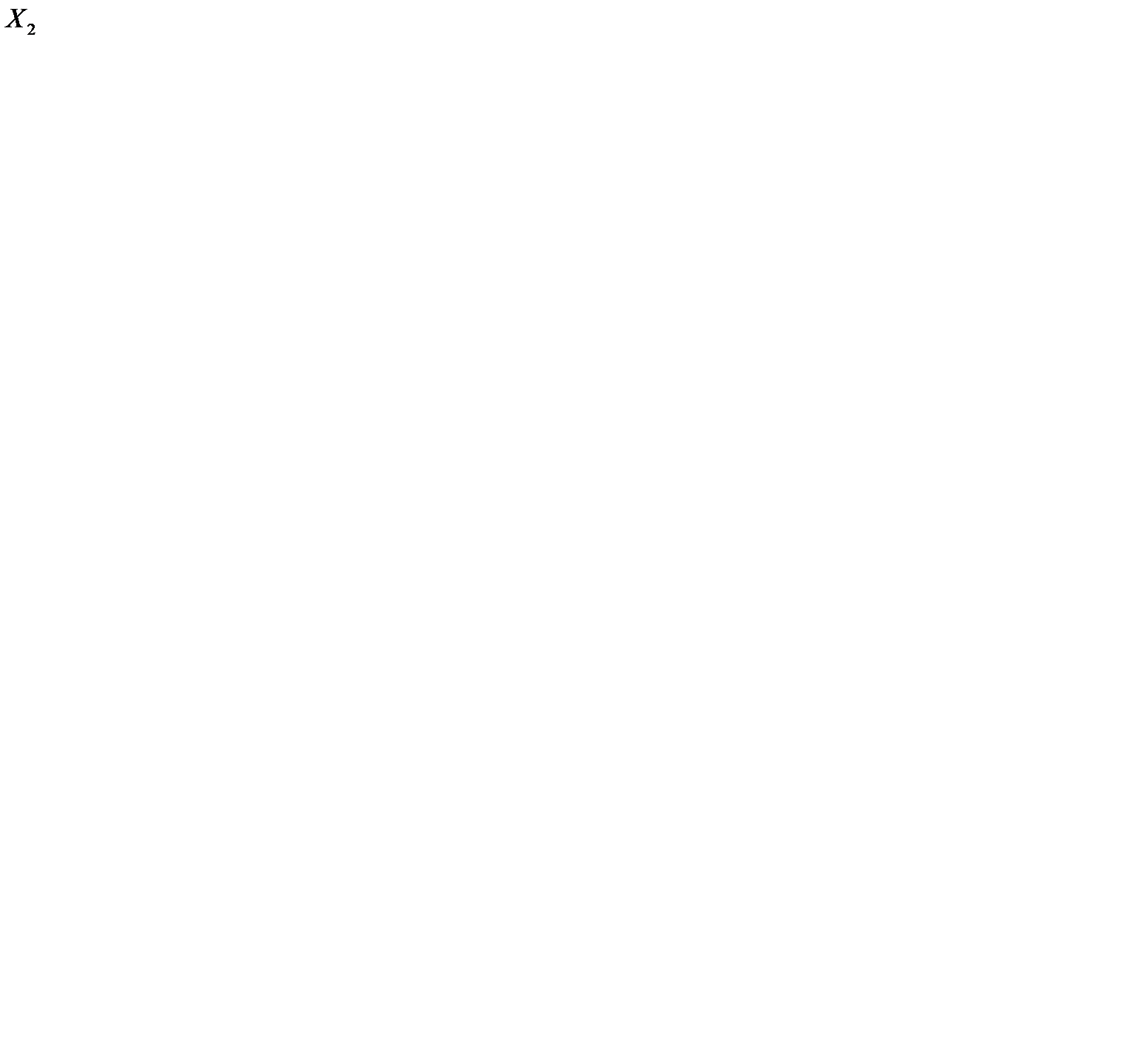
88989,98		99,8	99,3	99,27	98,89	100,4	100,5	100,4	99,49	99,73	100,25
81594,77		95,54	95,23	95,32	95,23	96,23	96,23	96,14	96,87	96,08	96,1
79834,5		94,33	94,36	94,45	94,51	94,82	94,85	94,88	94,86	94,93	95,01
68635,4		87,7	87,56	87,75	87,84	88,55	88,64	88,67	88,62	88,81	88,95
29671,4		58,00	58,26	58,72	59,11	59,94	60,33	60,7	61,02	61,47	61,91
464,89		17,96	6,9	8,3	0,63	-8,43	-1,1	13,24	8,01	8,905	9,993
		1,0009	1,9999	3,000	4,0000	4,9999	6,0000	7,0000	8,0000	9,0000	10,0000

В данном разделе исследуется также эффективность известных алгоритмов случайного поиска по сравнению с предлагаемым методом случайного поиска с регулируемой величиной спуска.

Рассмотрим задачу отыскания минимума функции многих переменных с ограничениями на аргументы следующими методами:

1) случайного поиска с пересчётом при переменной длине шага;

2) стохастическим вариантом наискорейшего спуска;

3) случайного поиска с регулируемой величиной спуска.

Стохастический вариант алгоритма наискорейшего спуска отличен от алгоритма случайного поиска с пересчетом тем, что значение приращения независимой переменной на (j+1) шаге не изменяется при условии:

(5.1)

где - длина шага поиска на (j+1) этапе;

- случайный вектор, компоненты которого являются независимые случайные величины, распределенные по равномерному закону в интервале

(-1,1).

Т.е. продолжается движение в ту же сторону до тех пор, пока будет смещение в «удачном» направлении.

На основании вышеизложенного работу первых двух алгоритмов можно представить следующим образом: в случае смещения в «неудачном» направлении (невыполнение условия 5.1) мы остаемся в предыдущей точке . В противном случае сдвигаемся в пространстве на , затем вырабатывается новое значение и т.д. – при использовании алгоритма случайного поиска с пересчётом. Если используется стохастический вариант наискорейшего спуска, то продолжаем двигаться в «удачном» направлении .

Отметим, что изложенные алгоритмы обладают достоинствами и недостатками. Например, стохастический вариант алгоритма наискорейшего спуска быстро находит экстремум функции в случае её монотонного характера (за счёт длительного спуска в «удачном» направлении), но в случае, если функция носит «овражный» характер, то работа алгоритма значительно замедляется. Противоположностью этого метода является алгоритм случайного поиска с пересчетом, который лучше проявляет себя, когда существенно нелинейная, и хуже, когда монотонна.

Анализируя эти два алгоритма, делается попытка найти метод, который объединял бы достоинства вышеуказанных методов, тем самым, обеспечивая более эффективный поиск экстремума широкого класса функций .

Блок-схема предлагаемого алгоритма случайного поиска с регулируемой величиной спуска приведена на рис.5.1 (символом J обозначено число шагов поиска, L - вспомогательная переменная). Заметим, что приведённая блок-схема при соответствует алгоритму случайного поиска с пересчетом и стохастическому варианту алгоритма наискорейшего спуска при .

Рассмотрим суть алгоритма случайного поиска с регулируемой величиной спуска. Он отличается от уже изложенных поисковых методов тем, что изменение "удачного" направления производится не на каждом шаге (как в алгоритме с пересчетом) и не при невыполнении условия (5.1) (как в стохастическом варианте алгоритма наискорейшего спуска), а при выполнении условия

Где - коэффициент спуска, .

Таким образом, спуск в удачном направлении продолжается до тех пор, пока текущее значение оптимизируемой функции не уменьшится в раз относительно величины функции, полученной при первом удачном шаге (при L=1).

Исследования проводились на тестовой функции вида

при ограничениях

имеющей экстремум при и

Сравнение эффективности работы алгоритмов производилось по двум

критериям: среднему числу вычислений оптимизируемой функции в зависимости от коэффициента спуска К_сп и среднему числу вычислений J_ср от

расстояния r начальной точки до точки экстремума . В каждой точке проводилось 10 экспериментов. Исследование проводилось при следующих начальных значениях:

1) начальный вектор ;

2) начальное значение длины шага поиска ;

3) критерий останова принят как

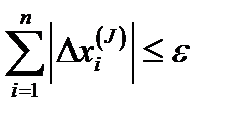при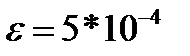

4) коэффициенты изменения шага .

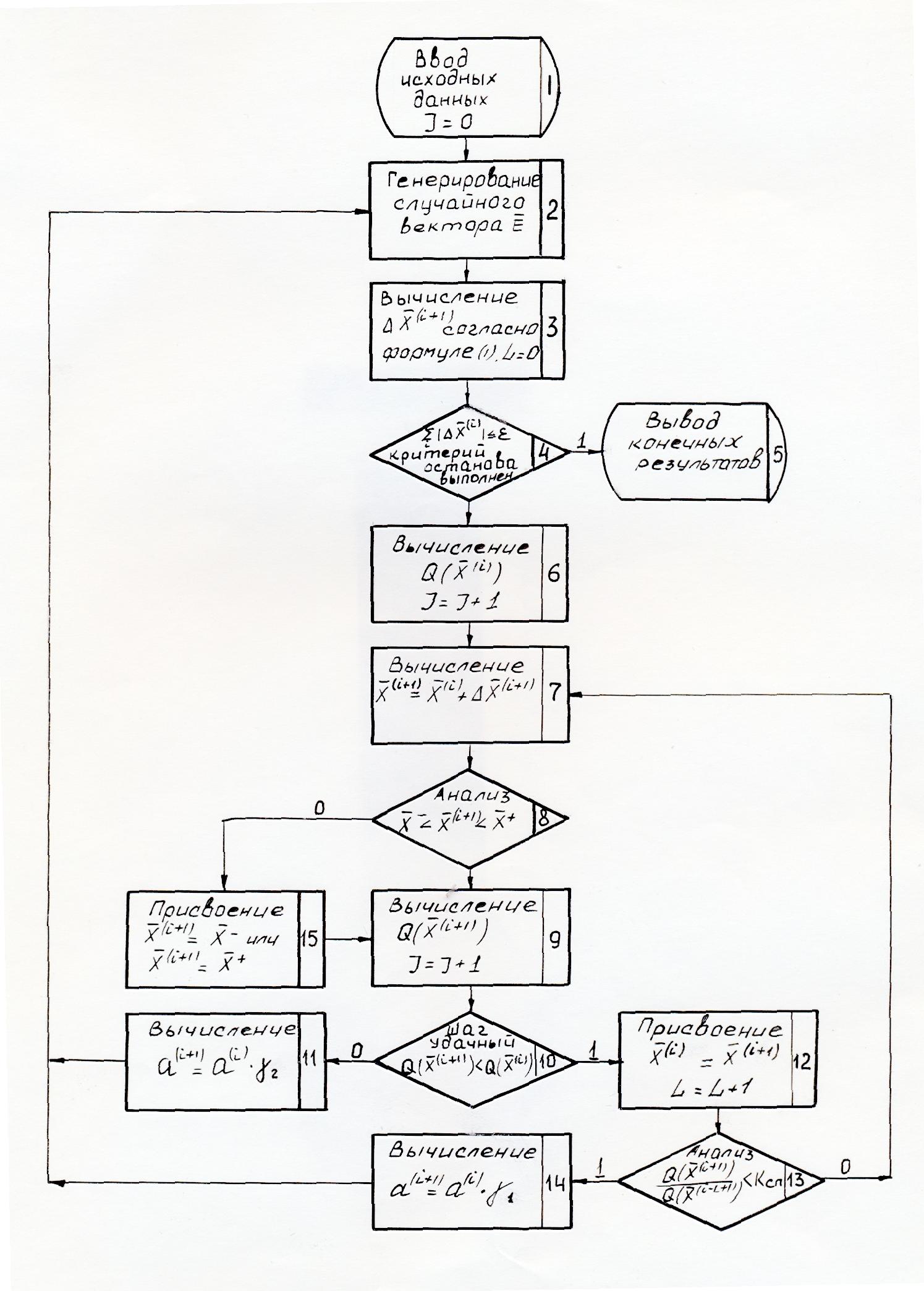
Рис.5.1 Блок-схема алгоритма случайного поиска

с регулируемой величиной спуска

1. Алгоритм С.П. с пересчётом при переменной длине шага

(5.2)

(5.3)

2. Стохастический вариант наискорейшего спуска при

(5.4)

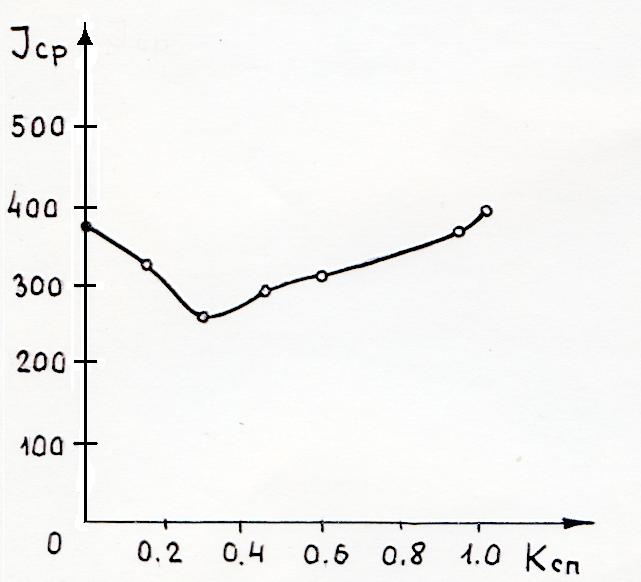
Рис. 5.2 Зависимость

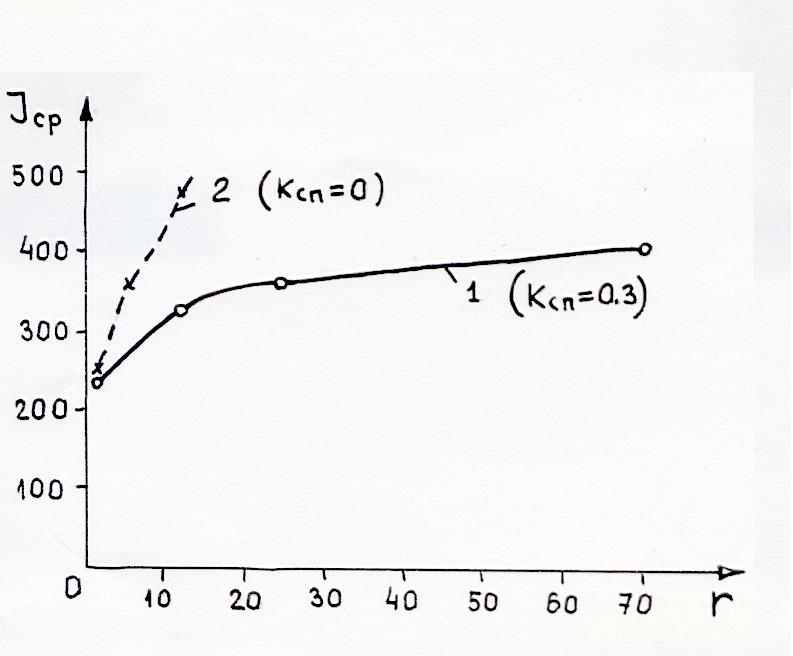
Рис. 5.3 Зависимость

Таблица№5.8

Характеристики			0,15	0,3	0,45	0,6	0,95
	29,3	19,9	40,9	31,2	40,5	12,5	17,8

Таблица№5.9

Характеристики			0,15	0,3	0,45	0,6	0,95
	6,68	19,55	34,65	26,98	21,53	7,17
		13,18	29,97	21,75	15,91	0,53	-7,16

Таблица№5.10

Характеристики		1,58	3,11	7,19	12,14	24,15	70,53
	40,5	32,9	40,9	40,7	24,5	16,7

Таблица №5.11

Характеристики при		1,58	3,11	7,19	12,14
	29,7	27,8	41,3	36,2

Результаты экспериментов представлены в таблице 5.8, где - среднеквадратичное отклонение от среднего числа вычислений оптимизируемой функции. График зависимости представлен на рис. 5.2.

По данным таблицы 5.8 можно построить таблицу 5.9, в которой отражены:

- процент снижения среднего числа вычислений в алгоритме случайного поиска с регулируемой величиной спуска к аналогичному критерию в других алгоритмах:

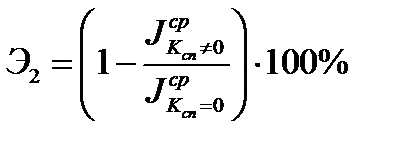
Из таблицы 5.9 следует, что при среднее число вычислений в предлагаемом алгоритме уменьшается на 34,65% по сравнению с алгоритмом случайного поиска с пересчетом и на 29,97% по сравнению с алгоритмом наискорейшего спуска, что говорит о преимуществе предлагаемого алгоритма по первому критерию эффективности.

Далее исследовалось влияние расстояния r от начальной точки до экстремального значения на среднее число вычислений оптимизируемой функции. Исследование проводилось при следующих начальных значениях:

1) коэффициент спуска ;

2) критерий останова принят при ;

3) коэффициенты изменения шага .

Результаты экспериментов представлены в таблице 5.10 (расстояние r вычислялось как ).

График зависимости приведён на рис. 5.3. Результаты расчётов показывают, что объём вычислений при увеличении r в стохастическом варианте алгоритма наискорейшего спуска возрастает значительно быстрее, чем в предлагаемом алгоритме.

5.2 Сопоставительный анализ методов НЛП в классе задач параметрической оптимизации САУ

Одной из центральных проблем, стоящих перед проектировщиком современных сложных систем управления, является моделирование объектов проектирования и анализ получаемых результатов с целью нахождения оптимального проектного решения. Применение ЭВМ позволяет задавать условия задачи в виде алгоритмов решения нелинейных дифференциальных уравнений, программ моделирования, оптимизации и т.п.

Не нашли, что искали? Воспользуйтесь поиском: