Вопрос 28. Окружность

Вопрос 15

Системы линейных уравнений с n-переменными.

Системы m-линейных уравнений с n-независимыми имеет вид

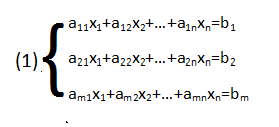
Где a_ij-это коэффициент при неизвестных, а b_i-это свободные члены или равные части уравнения

Систему (1) можно кратко записать в виде

_ijxj= bi, i= (2)

Решением системы (1) наз-ся совокупность n-чисел x1,x2,…, xn при подстановке которой в систему (1) каждое уравнение обращается в верное равенство. Система уравнений называется совместной, если она имеет решение и несовместной, если не имеет решений.

Совместная система наз-ся определенной, если она имеет единственное решение и неопределённой, если она имеет более одного решения.

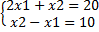совместная и определенная, т.к. имеет ед. решение (10;0)

несовместимая

совместная, но не определенная

Две системы ур-ний равносильными или эквивалентными, если они имеют одно и то же множество решений.

Запишем систему (1) в матричной форме.

, B= ()

Где A-матрица коэф. при неизвестных

В-матрица столбец свободных членов.

Тогда систему (1) можно записать Ax=B (3)

Система m-линейных уравнений с n-переменными. Там же, метод обратной матрицы Вопрос 16. Пусть число уравнений системы (1) равно числу переменных m=n, тогда матрица системы является квадратной, а ее определитель ∆=|A|называется определителем системы.

Рассмотрим решение системы двух уравнений с двумя неизвестными.

(4) | исключим переменную x2, умножив 1 ур-е на а22 второе-на (-а21) и сложить.

Исключим переменную х1, умножив 1ур-е (-а21), 2 ур-е-на а11 и сложить

В результате получим систему

(5)

Выражение в скобках есть определитель

∆1=a₁₁a₂₂-a₂₁a₁₂=_ ₊

∆2=a11b2-a21b1=_ ₊

(6)

Из полученной системы следует, что если определитель системы ∆ отличен от нуля, то система (4) имеет единственное решение опред-е по формуле x1= , x2=

Частные случаи:

1)Если ∆=0, ∆1≠0, или ∆2≠0, то система (4) несовместная

2)Если ∆=∆1=∆2=0, то система (4) неопределенная, имеет бесчисленное множество решений.

Для получения решения системы (1) при m=n в общем виде методом обратной матрицы предположим, что квадратная матрица системы –невырожденная, т.е. ее определитель |A|≠0. В этом случае сущ-т обратная матрица А^-1. Умножая обе части матрицы равенства АХ=В на А^-1 получим А^-1(АХ)=А^-1В. Т.к. по определению обратной матрицы

А^-1(АХ)= АА^-1Х=ЕХ=Е, то решением системы методом обратной матрицы будет матрица столбец

Х=А^-1В (7)

Вопрос 17. Правило Крамера.

Теорема. Пусть ∆-определитель матрицы А(∆=|A|), ∆j-определитель матрицы, получаемой из матрицы А с заменой j-го столбца столбцом из свободных членов. Тогда при ∆≠0 система имеет единственное решение, опр-е по формулам

xj= (8), j=

Формулами Крамера наз-ся формула (8)

Доказательство:

A^-1= * , где -присоединенная матрица.

Т.к. элементы есть алгебраические дополнения элементов матрицы A^I транспонированной к A, то запишем равенство Х=А-¹В (7) в развернутом виде

()= ()*()

Т.к. |A|= ∆ после умножения матриц получим ()= ()

Отсюда следует, что любого j=1,n

x_j= (b₁A_ij+b₂A_2j+…+b_nA_nj)

b₁A_ij+b₂A_2j+…+b_nA_nj =∆j, где j –определитель матрицы, полученной из матрицы A с заменой j-го столбца столбцом из свободных членов

Xj= .

Вопрос 21. Деление отрезка в данном отношении.

Пусть на плоскости задан М₁М_2.

И пусть М-любая точка этого отрезка, не совпадающая с концами

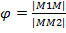(4)

λ- отношение в котором точка М делит отрезок М1М2.

Задача о делении отрезка в данном отношении состоит в том, что по данному отношению λ и данным координатам М1 и М2 находятся координаты точки М

Теорема. Если точка М от (х;у) делит отрезок М1М2 в отношении λ, то координаты этой точки

y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 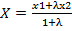, y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 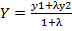(5)

Доказательство:

Опустим перпендикуляр из точки М1, М и М2. Обозначим через Р1, Р, Р2-основания этих перпендикуляров. На основе теории о пропорц. отрез. прямой заключается между параллельными прямыми:

|P1P|=|X-X2|, |P-P2|=|X2-X|

Т.к. значение под модулем одинакового знака, то можно записать

=> => x=

Получить 2-ю из (5) аналогично, спроектировать координаты точки на ось у.

Если М-середина отрезка М1М2, то λ=1 и по формулам (5) координаты отрезка находятся формулой (5).

Вопрос 22. Полярная система координат.

Состоит их точки О(полюс) и исходящего из него луча ОЕ(полярный курс). Пусть М-производная точка плоскости, -расстояние точки М от О, ϕ-угол, на коэф. которого нужно поверн. полярн. ось.

Установим связь между полярными координатами точки М(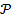;у) и (х;у).

При этом будем предполагать, что начало координат нах-ся в полюсе, а полож. Ось абсцисс совпадает с полярной осью.

Пусть М имеет прямоугольн. коорд. ху М(ху) и поляр. коорд. М(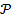; ϕ)

Из чертежа:

о рмулы (1) выражают прямоугол. Коорд. Через полярн.

Или выраж. пол. коорд. через тр-гольн. форм. 1

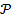=√x₂²+y₂² tg ϕ= (7)

Заметим, что tg ϕ определяет два значения половины угла ϕ, т.к. ϕ меняется от 0 до ∏. Из этих 2-х значений … правило, которое выполняет равенство (1)

Вопрос 23. Уравнение прямой с угловым коэффициентом.

Уравнение F(x;y)=0, называется уравнение линейной L, заданной в системе координат. Если ему удовл-т координаты изображаемой точки, лежащей на линии L и не удовлетворяют координаты точки не лежащей на этой линии. Линия L может опред. ур-м вида F( ϕ)=0. ϕ- полярные координаты точки.

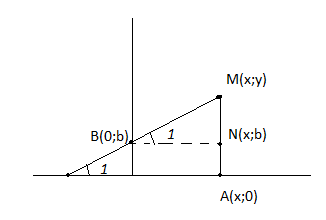1=

Пусть прямая пересекает ось ОУ. В точке В с координатами 0 и b B(0;b) и образует с осью ОХ угол : 0< <∏/2

Возьмем на прямой произвольную точку М с координатами (х;у), тогда tg -угол наклона прямой tg (1)

Введем угловой коэффициент k= tg

k= => y=kx+b (2)

Справедливо при условии ∏/2< <∏ ур-е прямой с углов. коэффициентом.

Рассмотрим частные случаи:

1.b=0 => y=kx-проход ч/з начало координат и образующей

При k= tg >0-острый угол с ОХ

При k<0- тупой угол

y=x-биссектриса 1-го и 3-го коорд. углов

y=-x-биссектриса 2-го и 4-го координатных углов

2.Если =∏/2, то прямая перпендикулярна оси ОХ и k= tg -не сущ-т, т.е. вертикальная прямая не имеет углового коэффициента.

3.Если =0, то k=tg0=0. Отсюда y=b-прямая параллельная оси OX.

Если прямая отсекает от OX, то ее уравнение будет x=a. А уравнение OY=X=0

Вопрос 24. Уравнение прямой, проходящей через данную точку в заданном направлении. Уравнение прямой, проходящей через две данные точки.

1) Пусть прямая проходит M1(x1;y1) и образует с осью OX угол x≠

Т.к. М1 лежит на прямой, то ее координаты удовлетворяют ур-ю

y₁= kx₁+b (3)

Вычитая (3) из (2) y=kx+b получаем уравнение искомой прямой

y-y1 =k(x-x1) (4)

Если прямая проход. М1 перпендикулярна ОХ, то ее углов. коэф-т равен бесконечности, и ее уравнение имеет вид x-x₁=0

2) Пусть даны точки М1 и М2

Запишем уравнение М1М2 в виде, где k-пост. Неизвестная углового коэф-та.

Т.к. прямая М1М2 проходит ч/з М1 ее координаты уд-т ур-ю(4)

y2-y1=k(x2-x1)

Отсюда вместо k подставим в 4 получим

y-y1= (x-x1)

Если y1≠y2, то ур-е можно переписать

(5)

Если y1=y2, то ур-е искомой прямой имеет вид:

y1=y2 => y=y1, в этом случае прямая параллельна ОХ

x1=x2, то прямая, проходящей точки имеет вид x1=x

Вопрос 25. Угол между прямыми. Условия параллельности и перпендикулярности прямых.

1. y=k1x+b1

y=k2x+b2, где k1=tg 1, k2=tg

Из геомет. рассмотр.

y= 2- 1, tgϕ=tg( 2- 1)= или tg = (6)

Формула (6) определяет один из углов между прямыми, а другой угол равен ∏-ϕ

2. Условия параллельности и перпендикулярности.

Если прямы L1 и L2-параллельны, то ϕ=0

k2-k=0 => k1=k2

Условия параллельности двух прямых является равенство их угловых коэффициентов.

Если L1 L2, то ϕ= . Отсюда -- tg = tg( 1)= -- ctg 1= -

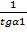
k2= --

Условия -ти 2-х прямых состоит в том, что их коэф. обратны по величине и общ. по знаку.

Вопрос 26. Общее уравнение прямой. Уравнение прямой в отрезках на осях.

1. Теорема:

В прямоугольной системе координат любой прямой задает уравнение 1-й степени

Ax+By+C=0

При любых А, В, С, где А, В не были нулями оба сразу, представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.

Док-во: Пусть В≠0, тогда ур-е можно записать в виде y = - x -

1.Если А≠0, С ≠0, получим y=kx+b

Если А≠0, С=0, y=kx-ур-е прямой, проходящей через начало координат.

Если А=0, С≠0, то y=b – прямая параллельна ОХ

Если А=0, С=0, то y=0 – ось OX

2.B=0, A≠0, тогда ур-е (7) примет x= -- ; ур-е прямой параллельной ОУ, а если С=0, то х=0 – ось ОУ.

Т.к. при любом значении А и В не равны одновременно 0, ур-е (7)-есть ур-е нек. прямой на плоскости ХОУ.

Линия определенная в прямоугольной системе координат ур-я 1-й степени- линия первого порядка.

2. Найдем уравнение прямой по заданным отрезкам а≠0, b≠0 от … на осях координат. Воспользуемся формулой прямой ч/з 2 заданные точки.

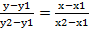
Подставим координаты точек в уравнение

или r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

Это ур-е наз-ся уравнением прямой в отрезках.

Вопрос 27. Нормально уравнение прямой. Расстояние от точки для прямой.

Пусть дана некоторая прямая L. Проведем ч/з начало координат прямую, перпендикулярную L и назовем ее нормалью. На нормали ведем направление от 0 к N, т.е. нормаль станет осью.

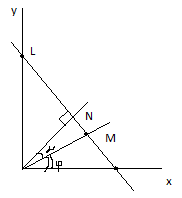
Обозначим ч/з α-угол на кот. нужно повернуть против часовой стрелки ось ОХ до совмещения положения напр. нормалями. p=ON. Выведем ур-е прямой L считая неизвест. число α и ρ:

Для этого возьмем на прямой L произвольную точку М с полярными координатами ρ и ϕ, где О-полюс, а ОХ-полярная ось.

Если точки O и N –не совпадают, то из тр-ка ONM находим

P= ρcos(α-ϕ)= ρ(cosαcosϕ+sinαsinϕ) или ρ*cosϕcosα+ ρ* sinϕsinα-P=0 (1)

Ур-е (1) есть ур-е прямой L в полярн. коорд……………………………………..

x=ρ*cosϕ, y=ρ*sinϕ

x*cosα+y*sinα-ρ=0 (2)

Если точки O и N cовпадают, то уравнение P=0 и уравнение принимает вид

x*cosα+y*sinα=0

Уравнение (2)- нормальное уравнение прямой L. Для того, чтобы привести общее уравнение прямой к нормальному виду (2) нужно все члены ур-я умножить на нормир. множитель μ.

Ax+By+C=0 (*)

μ =

Перепишем

μA=cosα, μB=sinα, μC= -p

Знак интегрирующего множителя берется противоположно знаку С. Если прямая L задана ур-м (2), а точка М₀(х₀;у₀)-не лежит на этой прямой, то расстояние от точки до прямой определяется как выражение

d=|x₀cosα+y₀sinα-p| (3)

Пусть даны М₀(х₀;у₀) и прямая L ур-м *

Под расстоянием от точки М₀до прямой L понимается длина перпендикуляра d=M₀N, опущенного из точки М₀ на прямую.

Для определения расстояния d необходимо:

1. Составить уравнение прямой M₀N, перпендикулярной L проходящей ч-з точку М_0.

2. Найти точку N (x;y)—пересечение прямых решив совместно ур-я M₀N и L/

3. Найти расстояние по формуле

Вопрос 28. Окружность

Изучение уравнении второго порядка, описываемы уравнениями второй степени. Начнем с окружности с центром O (x_o;y_o), радиусом R и точкой M(x₁;y₁).

По определению, для любой точки М окружности вып-ся равенство |OM|=R.Используя формулу расстояния между двумя точками получим:

√(x-x_o)²+(y-y_o)²=R или то же самое (x-x_o)²+(y-y_o)²=R² (5)-нормальное ур-е окружности.

В частности если центр окружности в начале координат, то ее ур-е x²+y²=R² .

Рассмотрим общее ур-е второй степени с 2 переменными:

Ax²+Bxy+Cy²+Dx+Ey+F=0 (6)

A²+B²+C²≠0? A,B,C-одновременно не 0.

Выясним, при каких условиях ур-е (6)- есть ур-е окружности. Для этого (5) раскроим скобки и запишем

x²+y²-2x_ox-2y_ox+x_o²+y_o²-R²=0 (7)

Для того, чтобы (6) и (7) описывают одну и ту же линию, необходимо, чтобы коэф-т В=0, т.к. ур-е (7) не содержит x,y, а……………………………..

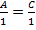=> A=C≠0

Получим: Ax²+Ay²+By+Ey+F=0 (8)

Уравнение (8) называется общим уравнением окружности.

Разделив обе части уравнения на А и заполнив члены содерж. х,у получим:

(x+ )² +(y+ 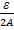)²= (𝒟²+ ² -4 AF)/4 A² (9)

Cсравнив (9) с уравнением окружности (5) можно сделать вывод, что (6) –есть уравнение окружности, тогда B=0, A=C и 𝒟²+ ² -4 AF >0.

При выполнении этих условий центр окружности расположен в точке O (

а R= √(𝒟²+ ² -4 AF)/2A.

Вопрос 29. Эллипс.

Эллипсом называется множество всех точек плоскости, сумма расстояний которых до 2х данных точек называемыми фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Обозначим F1 и F2-фокусы эллипса. Расстояние |F1F2|=C. Сумму расстояний от производной точки эллипса до фокусов обозначим через 2а.

По определению эллипса а>c, Для вывода уравнения эллипса введем параллельную систему координат к, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило F1F2 пополам.

Пусть M(x;y)- произвольная точка плоскости. Обозначим расстояние r1=|F1M|, r2=|F2M|

Из определения эллипса следует, что точка M(x;y) будет лежать на эллипсе когда r1+r2=2a (1)

По формуле расстояние между 2мя точками мы можем переписать

=2a (3)

Урвнение (3)-есть ур-е эллипса. Но оно неудобно для использования.

Преобразуем:

Перенесем один радикал вправо и возведем обе части в квадрат.

Получим:

(x+c)² + y²=4a²-4a +(x-c)²+y²

Приводя подобные члены, получим:

a√((x-c)²+y²)=a²-cx (4)

Снова возведем обе части в квадрат

После упрощения получим:

(a²-c²)-x²+a²y²=a²(a²-c²) (5)

Обозначим ч/з b=√(a²-c²), тогда (5) ур-е примет вид: b²-x²+a²y²=a²b²

Разделив обе части на a²b², окончательно получим x²/a²+y²/b²=1 (6)

Любая точка координат которая удовлетворяет (6)-есть уравнение эллипса. Уравнение (6) называется каноническим уравнением эллипса.

Заметим, что (6) содержит только четные степени, поэтому эллипс симметричен относительно осей OX и OY и относительно начала координат. Т.о., чтобы знать формулу всего эллипса достаточно установить вид той части его, которая лежит в первом квадрате.

Для этой части y≥0 (6)=>

y= (7) Из (7) следует:

1.если x=0, то y=b, следовательно B(0;b) лежит на эллипсе

2. при возрастании числа x<a, b<y<0

3.если x=a => y=0, следовательно точка A(a;0) лежит на эллипсе

4. когда x>a => a2-x2<0, следовательно x>a на эллипсе нет.

Итак, частью эллипса распол. В первой координатном угла является дуга BA. Проведя симметрию относительно начала координат и оси получим эллипс.

Если a=b, ур-е => x²+y²=a² (эллипс-окружность). Оси симметрии наз-ся осями эллипса, а центр симметрии O –центром эллипса точки в которых эллипс пересек. оси-его вершина.

Величины a,b=большая и малая полуось эллипса. Эксцентриситетом эллипса называется отношение , где с-половина расстояний м/у фокусами, а-большая полуось эллипса. Т.к. с<а, то 0≤ E≤ 1.

Принимая во внимание, что c²=a²-b²

E ²= = = 1-()² => =

И легко получится геометрическое истолкование эксцентриситета эллипса.

Т.о. эксцентриситет эллипса характеризует мру вытянутости эллипса. Как известно, планеты, нек. кометы движутся по эллипсическим траекториям. Оказывается, что эксцентриситеты планетарных орбит весьма малы, а кометы велики, то есть близки к 1.

Т.о., планеты движутся почти по окружности, а кометы приближаются к солнцу. Солнце находится в одном из фокусов, но значительно отдалено от него.

Вопрос 30. Гипербола.

Гиперболой называется множество всех точек плоскости, для которого модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная меньшая чем расстояние между фокусами, обознач. через F1 и F2, а расстояние между фокусами.

|F1F2|=2c, модуль разности расстояния от произвольной точки гиперболы до фокуса через 2а.

По определению 2a<2c или a<c.

Введем прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило отрезок F1F2 пополам. Тогда фокусы гиперболы имеют координаты F1(-c;0), F2(c;0).

Выведем уравнение гиперболы. Пусть M(x;y) произвольная точка плоскости.

Числа |F1M|, |F2M| фокальными радиусами точки М и обозначается через r1,r2.

По определению |r1-r2|=2a (1) r1-r2= 2a

По формуле расстояния между двумя точками

(2)- уравнение гиперболы.

Преобразуем его. Перепишем один радикал вправо и возведем обе части в квадрат.

(c²-a²)x²-a²y²=a²(c²-a²) (3)

b²=c²-a² b²x²-a²y²=a²b²

(4)

Уравнение (4) называется каноническим уравнением гиперболы. Исследуем гиперболу по ее каноническому уравнению. Т.к. уравнение (4) содержит члены только с четными степенями ху, то гипербола симметрична относительно ху и относительно начала координат. Поэтому достаточно рассмотреть часть гиперболы, лежащей в первом координатном угле. На этой части y ≥0. Поэтому разрешая (4) уравнение относительно (у), получим

(5)

Из (5) следует:

1.Если 0≤x≤a, то x²-a²<0, следовательно, точки гиперболы с такими координатами нет.

2.Если x=a, то y=0, следовательно точка A(a;0) лежит на гиперболе.

3.Если x>a, то y>0, причем y возрастает с возрастанием x и y стремится к ∞, при x стремящегося к ∞.

Переменная точка M(x;y) на гиперболе движется с ростом x вправо и вверх, а ее начальное положение A(a;0), причем точка M(x;y), уходя по гиперболе в ∞, неограниченно приближается к прямой

(6) называемой асимптотой гиперболы.

Вид гиперболы легко установить, используя симметрию относительно координатных осей. Гипербола имеет вид ветви и две асимптоты.

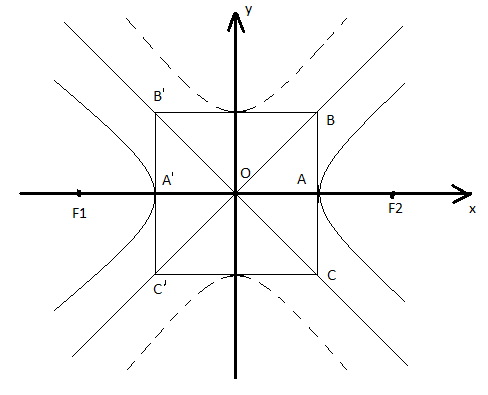
Оси симметрии называются осями гиперболы, а центр симметрии О-центром гиперболы. Точки А и А^{l –}вершины гиперболы. Прямоугольник BB^lC^lC со сторонами 2a и 2b называется основным прямоугольником гиперболы.

Величина a,b наз-ся действительной и мнимой полуосями гиперболы:

также определяет гиперболу.

Она изображена пунктиром. Вершина ее лежит на оси ОУ. Эта гипербола называется сопряженной по отношению к гиперболе (4)

Гипербола с одинаковыми полуосями называется равносторонней, и ее каноническое уравнение имеет вид x²-y²=a².

Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Эксцентриситетом гиперболы называется решение . Чем меньше эксцентриситет, тем больше прямоугольник вытянут в направлении действительной оси.

Вопрос 31. Директрисы эллипса и гиперболы.

Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра от него называются директрисами эллипса.

Уравнение директрисы эллипса, заданного каноническим уравнением имеют вид:

Т.к. для эллипса E<1, то отсюда следовательно правая директриса расположена правее правой вершины эллипса, а левая-левее его левой вершины.

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстояние от него называются директрисами гиперболы. Ур-я

Для гиперболы E>1 что правая директриса расположена между центром и правой вершиной гиперболы, а левая-между центром т левой вершины.

С помощью директрисы и эксцентриситета можно сформировать общее свойство, присущее эллипсу и гиперболе.

Множество всех точек, для которых отношение расстояния до фокуса и соответственно директрисы является величиной постоянной, равной =E-есть эллипс, если E>1 и гипербола, если E>1.

Возникает вопрос: что представляет собой множество точек, при условии E=1.

Оказывается это линия второго порядка, называемая гиперболой.

Вопрос 32. Парабола.

Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Для вывода уравнения параболы введем прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус директрисе.

Начало координат расположен посередине между фокусом и директрисой. Пусть M(x;y)-произвольная точка плоскости, r-расстояние от точки M до фокуса F. d-расстояние от M до директрисы. p –расстояние от фокуса до директрисы.

Величину p называют параметром параболы. По определению, точка M будет лежать на параболе, если r=d (7).

Фокус F имеет координаты (;0), поэтому r=|FM|= . Расстояние d выражается равенством d=|MQ|=x+ . Последняя формула верна для x≥0. Если x<0, то r>d и такая точка на параболе не лежит.

Из (7) имеет:

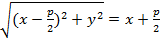(8) – уравнение параболы.

Приведем его к более удобному виду, возведя обе части в квадрат

(9)-уравнение параболы.

Уравнение (9) называется каноническим уравнением параболы.

Исследуем параболу по уравнению (9). Т.к. (9) содержит y в четной степени, то парабола симметрична относительно ОХ, поэтому достаточно рассмотреть ее част., лежащую в верхней полуплоскости. Для этой части y≥0.

(10)

Отсюда следует, что:

1.Если x<0, то под корнем отрицательное выражение, следовательно, левее оси OY нет ни одной точки параболы (10).

2.Если x=0, то y=0 и начало координат лежит на параболе и является ее самой левой точкой.

3. При возрастании x, возрастает y, причем, если x→∞, то y может →∞.

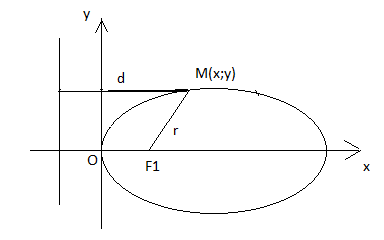
Т.о. производя симметрическое отражение в рассматриваемой части относительно оси OX, получим всю параболу.

Точка О называется вершиной параболы, а ось симметрии-осью параболы. Число p выражает расстояние от F до директрисы и характеризует ширину области, ограниченной параболой.

Парабола в уравнении которой y²= -- 2px, p>0 располагается слева.

Вершина этой параболы совпадает с началом координат и осью симметрии является ось ОХ- Уравнение параболы.

Вопрос 18 Метод Гаусса.

Рассмотрим решение системы m-линейных уравнений с n-переменными в общем виде.

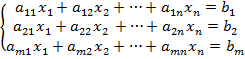(1)

Метод Гаусса-метод последовательного исключения переменных заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Предположим, что в системе (1) коэффициент при переменной x₁ в первом уравнении a₁₁≠0 (если это не так, то этого можно добиться перестановкой уравнений местами).

Шаг 1. Умножая первое уравнение на числа -a₂₁/a₁₁, -a₃₁/a₁₁,…,-a_m1/a₁₁ и прибавляя полученные уравнения соответственно ко второму, третьему,…,m-му уравнению системы (1), исключим переменную x₁ из всех последующих уравнений, начиная со второго. Получим:

(2)

Где буквами с верхним индексом ⁽¹⁾ обозначены новые коэффициенты, полученные после первого шага.

Шаг 2.Преположим, что a22(1)≠0. Умножая второе уравнения на числа –a₃₂⁽¹⁾/a₂₂⁽¹⁾, --a₄₂⁽¹⁾/a₂₂⁽¹⁾,…,-- a_m2⁽¹⁾/a₂₂⁽¹⁾ и прибавляя полученные уравнения соответственно к третьему, четвертому,.., m-му уравнению системы (2), исключим переменную x₂ из всех последующих уравнений, начиная с третьего.

Продолжая процесс последовательного исключения переменных x₃,x₄,…,x_r-1,после (r-1)-го шага получим систему:

a₁₁x₁+a₁₂x₂+…+a_1rx_r+…+a_1nx_n=b₁

a₂₂⁽¹⁾x₂+…+ a_2r⁽¹⁾x_r+…+a_2n⁽¹⁾x_n=b₂⁽¹⁾… (3)

a_r^(r-1)+…+a_rn^(r-1)x_n=b_r^(r-1)

0=b_r+1^(r-1)

0=b_n^(r-1)

Число ноль а последних m-r уравнениях означает, что их левые части имеют вид O*x₁+O*x₂+…+O* x_m. Если хотя бы одно из чисел b_r+1,…,b_m^(r-1) не равно нулю, то соответствующее равенство противоречиво, и система (1) несовместима.

Т.о., для любой совместной системы числа b_r+1^(r-1),…,b_m^(r-1) В системе (3) равны нулю. В этом случае последние m-r уравнений в системе (3) являются тождествами и их можно не принимать во внимание при решении системы (1). Очевидно, что после отбрасывания «…» уравнений возможны два случая: а)число уравнений системы (3) равно числу переменных, т.е. r=n. В этом случае, система (3) имеет треугольный вид; б)r<n, в этом случае система (3) имеет ступенчатый вид.

Переход от системы (1) к равносильной системе (3) называется прямым ходом метода Гаусса, а нахождение переменных из системы (3)-обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразованная не с самими уравнениями, а с матрицей их коэффициентов. Для этого рассматривают матрицу:

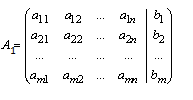
называемую расширенной матрицей системы (1), т.к. в нее дополнительно включен столбец из свободных членов.

Запрос о разрешимости системы (1) в общем виде рассматривается в ……

Теорема Кронекера – Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Для совместных систем линейных уравнений верны следующие теоремы:

1.Если ранг матрицы совместной системы равен числу переменных, т.е r=n, то система (1) имеет единственное решение.

2.Если ранг матрицы совместной системы меньше числа переменных, т.е r<n, то система (1) неопределенная и имеет бесконечное множество решений.

2 вариант. Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.

Система т линейных уравнений с п неизвестными имеет вид:

x ₁, x ₂, …, x_n – неизвестные.

a_{i j} - коэффициенты при неизвестных.

b_i - свободные члены (или правые части)

Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными, если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

(1)

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁. Получим уравнение:

(2)

где

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а ₂₁ и а ₃₁).

Система примет вид:

(3)

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂ из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

(4)

где

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

В результате преобразований система приняла вид:

(5)

Система вида (5) называется треугольной.

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.