Деление комплексных чисел, формула.

Модуль и аргумент

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа обозначается и определяется выражением 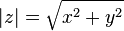. Часто обозначается буквами или 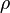. Если является вещественным числом, то совпадает с абсолютной величиной этого вещественного числа.

Для любых имеют место следующие свойства модуля.:

1) , причём 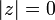тогда и только тогда, когда ;;

2) 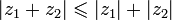(неравенство треугольника);

3) ;

4) .

Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .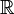

5) Для пары комплексных чисел и модуль их разности равен расстоянию между соответствующими точками комплексной плоскости.

Угол (в радианах) радиус-вектора точки, соответствующей числу , называется аргументом числа и обозначается .

• Из этого определения следует, что ; ; .
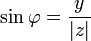• Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до , где — любое целое число.
• Главным значением аргумента называется такое значение , что . Часто главное значение обозначается ^[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: .

3)

Произведением комплексных чисел и называется комплексное число

§

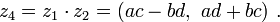
Так же как и в случае вещественных чисел, для знака умножения используют ; часто его вовсе опускают: .

П

Пример. , , .

В отличие от суммы комплексных чисел, определение произведения кажется довольно искусственным. Ответ на вопрос

4)

Деление комплексных чисел, формула.

В соответсвии с определением деления действительных чисел устанавливается следующее опреденеие. Разделить комплексное число a + b·i (делимое) на комплексное число a′ + b′·i (делитель) - значит найти такое число x + y·i (частное), которое, будучи помножено на делитель, даст делимое.

Если делитель не равен нулю, то деление всегда возможно и частное единственно.

Частное комплексных чисел a + b·i, и a′ + b′·i вычисляется по формуле:

5)

Не нашли, что искали? Воспользуйтесь поиском: