Миноры и алгебраические дополнения. Теорема Лапласа

Минором Мij квадратной матрицы n-го порядка для элемента аij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца.

Алгебраическое дополнение элемента 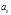определителя определитель

где - минор

элемента .

Теорема Лапласа. В данной квадратной матрице А(n x n) вычеркнем k строк (1£k£n). Тогда равно сумме произведений всевозможных миновров к-того порядка из данных строк на их алгебраические дополнения: . То же для столбцов. Теорема удобна для матриц с большим кол-вом нулей.

4.Определители n-го порядка. Их свойства и методы вычисления.

Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца.

Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей: если оно четное «+», нечетное «-».

Инверсия - когда большее число стоит перед меньшим.

Св-ва определителей:

1. В определителе строки и столбцы равнозначны.

2. Если все Эл-ты в строке или столбце = 0, то определитель =0.

3. Общий множитель строки или столбца можно выносить.

4. Если в определителе переставить местами 2 строки, то знак определителя изменится на противоположный.

5. Если в определителе 2 одинаковых строки/столбца, то определитель =0.

6. Если в определителе 2 строки пропорциональны, то определитель =0.

7. Определитель можно разложить на сумму.

8. Если в определителе некоторая строка/столбец является линейной комбинацией другой строки-столбца, то определитель =0.

9. Если к Эл-ам некоторой строки добавить соотв. Эл-ты другой строки умноженные на число не равное 0, то определитель не изменится.

Минор- определитель полученный из определителя n-го порядка вычеркиванием К каких-то строк и К столбцов.

Теорема Лапласа.

Определитель n-го порядка равен сумме произведений Эл-ов некоторой строки/столбца на их алгебраические дополнения.

Алгебраическое дополнение – A_ij=(-1)^i+jM_ij

Определитель треугольного вида равен произведению Эл-ов главной диагонали.

6.. Обратная матрица. Достаточное условие существования обратной матрицы. Определим операцию деления матриц как операцию, обратную умножению.Опр. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

7. «Матричная форма заииси системы линейных алгебраических уравнений»

Линейной системой mуравнений сn неизвестными, называется система вида:

(1), гдеa_ij, h_i (i=1,m; j=1,n) – числа.

Заметим, что a_ij - коэффициент при неизвестном x_j в i-ом уравнении системы, h_i – свободный член в i-ом уравнении системы (1). Матрица A = составленная из коэффициентов при неизвестном сист. (1) – называется матрицей, или основной матрицей системы, а матрица = , которая получается из матрицы А приписыванием свободных членов, называется расширенной матрицей системы (1).

Для того, чтобы записать систему (1) в матричной форме, наряду с матрицей системы А рассмотрим следующие матрицы:

X= ; H = ;, т.к. матрица А согласованна с матрицей Х, то можно найти произведение А*Х=Н. Элементами полученной матрицы-столбца, являются левые части уравнения системы (1). На основании определения равенства матриц, систему (1) можно записать в виде матричного уравнения;

А*Х=Н (2) – такая запись называется матричной.

8. «Матричный метод для решения не вырожденных систем»

Матричный метод решения систем линейных уравнений.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений: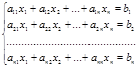

Составим матрицы: A= ; B = ; X = .

Систему уравнений можно записать:

A×X = B.

Сделаем следующее преобразование: A^-1×A×X = A^-1×B,

т.к. А^-1×А = Е, то Е×Х = А^-1×В

Х = А^-1×В

Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.

9.Формулы Крамера.

Система линейных уравнений:

Определители: Решение:

Не нашли, что искали? Воспользуйтесь поиском: