Зам предел. Второй замечательный предел

или

Доказательство второго замечательного предела:

Доказательство для натуральных значений

Докажем вначале теорему для случая последовательности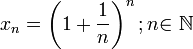

По формуле бинома Ньютона:

Полагая , получим:

(1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины возрастают. Поэтому последовательность 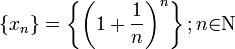— возрастающая, при этом

(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

Поэтому (3).

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3): .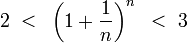

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 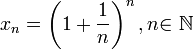монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: , поэтому

.

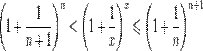Если , то 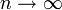. Поэтому, согласно пределу , имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть 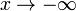. Сделаем подстановку , тогда

.

Из двух этих случаев вытекает, что для вещественного x.

42.непрерывные функции. Точки разыва. Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения. ε-δ определение

Пусть и .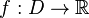

Функция непрерывна в точке 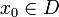, если для любого существует такое, что для любого

Функция непрерывна на множестве 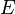, если она непрерывна в каждой точке данного множества.

Не нашли, что искали? Воспользуйтесь поиском: