
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Уравнение прямой проходящей через данную точку и перпендикулярную данному вектору
| l |
| n |
| M0(x0;y0) |
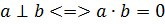
M0M= 
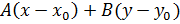

Общее уравнение прямой



Вопрос 2.
Эллипс.
Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 есть заданная постоянная величина, называется эллипсом.
Каноническое уравнение эллипса.
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
 .
.
где (a и b – положительные действительные числа)
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Число a называют большой полуосью эллипса, а число b – его малой полуосью.
Свойства эллипса:
Фокальное свойство. Если F 1 и F 2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F 1 X) равен углу между этой касательной и прямой (F 2 X).
Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
Эксцентриситетом эллипса называется отношение. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Эллипс также можно описать как
фигуру, которую можно получить из окружности, применяя аффинное преобразование
ортогональную проекцию окружность на плоскость.
Пересечение плоскости и кругового цилиндра.
Вопрос 3.
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.
Простейшее уравнение гиперболы



Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.
Если 2 c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение
a 2 + b 2 = c 2.
При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид
x 2 - y 2 = a 2.
Фокусы гиперболы лежат на ее действительной оси.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.

Асимптоты гиперболы - две прямые, определяемые уравнениями


Напомним, что асимптотой кривой, имеющей бесконечную ветвь, называется прямая, которая обладает тем свойством, что когда точка по кривой удаляется в бесконечность, ее расстояние до этой прямой стремится к нулю.
Вопрос 4.
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.
Простейшее уравнение параболы
y 2 = 2 px.
Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.
Координаты фокуса F параболы  . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы
. (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы

Эксцентриситет параболы e = 1.

y 2 = 2 px (p > 0)
Вопрос 5.
Векторы:
Множество чисел u1…un пронумерованы и расставлены в порядке возрастания их номеров.
N-мерным вектором называется последовательность из n чисел эти числа координаты вектора.
Число n координат вектора – размерность вектора.
Обозначение:
A= 
A= 
Специальные векторы:

Единичный вектор:
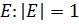
Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов.
aji - элемент матрицы, который находится в i-ой строке и j-м столбце.
Матрици специального вида:


 – квадратная
– квадратная
 - прямоугольная
- прямоугольная
Верхнетреугольная матрица – квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица – квадратная матрица, в которой все элементы выше главной диагонали равны нулю.
Общий вид треугольных матриц:

Операции над матрицами:
Пусть  и
и  — матрицы одинаковых размеров
— матрицы одинаковых размеров  . Матрица
. Матрица  тех же размеров
тех же размеров  называется суммой матриц
называется суммой матриц  и
и  , если ее элементы равны сумме соответствующих элементов матриц
, если ее элементы равны сумме соответствующих элементов матриц  и
и  :
: 

 . Сумма матриц обозначается
. Сумма матриц обозначается  . Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно
. Операция сложения матриц определена только для матриц одинаковых размеров и выполняется поэлементно
Произведением матрицы  на число называется матрица
на число называется матрица  тех же размеров, что и матрица
тех же размеров, что и матрица  , каждый элемент которой равен произведению числа на соответствующий элемент матрицы A.
, каждый элемент которой равен произведению числа на соответствующий элемент матрицы A.
Операции сложения матриц и умножения матрицы на число называются линейными операциями над матрицами. Непосредственно из определений вытекают следующие свойства линейных операций.
Для любых матриц  одинаковых размеров и любых чисел
одинаковых размеров и любых чисел  справедливы равенства:
справедливы равенства:
1.  (коммутативность сложения);
(коммутативность сложения);
2.  (ассоциативность сложения);
(ассоциативность сложения);
3. существует нулевая матрица  (тех же размеров, что и
(тех же размеров, что и  ):
):  ;
;
4. существует матрица  , противоположная матрице
, противоположная матрице  ;
;
5.  ;
;
6. 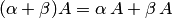 ;
;
7.  ;
;
8.  .
.
Вопрос 6.
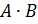 если число строк 2 матрицы = числу столбцов 1 матрицы – это условие согласованности для умножения.
если число строк 2 матрицы = числу столбцов 1 матрицы – это условие согласованности для умножения.

Свойства умножения матриц:
Пусть  – любое число, A,B,C - произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:
– любое число, A,B,C - произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:
1.  ; (ассоциативность умножения матриц)
; (ассоциативность умножения матриц)
2.  ; (дистрибутивность умножения)
; (дистрибутивность умножения)
3. 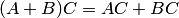 ; (дистрибутивность умножения)
; (дистрибутивность умножения)
4.  .
.
5.  и AB =
и AB =  тогда А и В делители нуля.
тогда А и В делители нуля.
Пример:

Не коммутативность умножения:



Следовательно  ч.т.д.
ч.т.д.
Вопрос 7.
Если поменять строки и столбцы A то Aт – операция транспонирования
Свойства транспонирования:
1. 
2. 
3. 
Вопрос 8.
Определитель – это отображение всех возможных квадратных матриц во множнство вещественных чисел.
Свойства:
1. Определитель произведения двух матриц равен произведению их определителей det (AВ) det A×det B.
2. При транспонировании матрицы ее определитель не меняется.
3. Если все элементы какого-либо столбца (строки) определителя равны нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое слагаемое содержит по одному и только одному сомножителю из каждого столбца (строки).
4. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.
5. Определитель равен 0 если он имеет две равные строчки и столбца.
6. Множитель можно вынести за знак определителя.
Способы нахождения определителя:
Способ треугольников для матрицы 3X3.

Универсальный метод нахождения определителя mXn.

Вопрос 9.
Любой n-мерный вектор x с координатами x1x2…xn называется решением линейного уравнения если при подстановке его координат уравнение обращается в верное множество решений.
Классификация ЛУ по количеству решений:
В общем случае имеет вид:

 – постоянные коэффициенты.
– постоянные коэффициенты.
Тогда решением СУ называется n-мерный вектор X=(x1,x2,…,xn) который является решением каждого из уравнений системы.
Две СУ называются равносильными если они имеют одно и тоже множество решений.
СУ называется совместной если она имеет хотя бы одно решение если не одного не совместна.
СУ – определена если имеет единственное решение.
СУ – неопределённая если она имеет бесконечное множество решений.
Метод Крамера (решение ЛУ с помощью определителя)
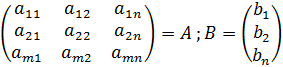
Пусть  определитель матрицы A, пусть
определитель матрицы A, пусть  обозначим |A| который получится из A если j столбец заменить на столбец в правой части
обозначим |A| который получится из A если j столбец заменить на столбец в правой части

т.е.  если
если  то решение единственное X=(x1,x2,…,xn) вычисляется по формуле:
то решение единственное X=(x1,x2,…,xn) вычисляется по формуле:
 – формула Крамера
– формула Крамера
Если 
a) 
b)  .
.
Вопрос 10.
X – разрешённая неизвестная для СУ если она входит в одно уравнение с коэффициентом +1, а в другие с коэффициентом 0.
Разрешённые неизвестные входящие в набор называются базисными, а не входящие свободными.
Общим решением СУ называется совокупность выраженных разрешённых неизвестных через свободные члены и неизвестные.
Частным решением СУ – которое получается из общего при конкретных значениях свободных переменных.
Базисным решением СУ – частное решение которое получается из общего при нулевых значениях переменных.
Общее решение – это набор формул, с помощью которых можно получить любое частное решение.
Алгоритм метода Гаусса:
Пусть есть система:

Метод Гаусса является прямым методом т.е. позволяет найти точное решение для невырожденной матрицы за вполне определенное количество операций.
Состоит из двух этапов, прямой ход - расширенная матрица приводится в треугольному виду, как на рисунке ниже:

Необходимым условием является то, чтобы на диагонали матрицы не было нулевых элементов.
А затем обратный ход - когда находятся все неизвестные вектора X, начиная с последнего.
Рассмотрим более подробно прямой ход.
1) Разделим первую строку расширенной матрицы на  :
:

2) Вычтем из второй строки расширенной матрицы произведение

на измененную первую строку матрицы:

3) Затем вычтем произведение первой строки на

из третьей,и так далее по строкам, пока матрица не примет вид:

4) Затем процесс повторяется - уже делением второй строки на a22*, столбец за столбцом, матрица приводится к верхнетреугольному виду.
После чего начинается обратный ход, тривиальным образом находя неизвестные X:

Вопрос 11.
Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Укажем следующие свойства обратных матриц:
1. (A-1)-1 = A;
2. (AB)-1 = B-1A-1

Вопрос 12.
Пример вывода формул:





(Использую Бином Ньютона:
 )
)

Вопрос 13.
Теорема Ферма
1. 
2. 
3. 
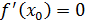
Не нашли, что искали? Воспользуйтесь поиском: