Схемы дедуктивных умозаключений

Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (п. 25), в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?

В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие:

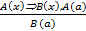- правило заключения;

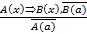- правило отрицания;

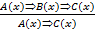- правило силлогизма.

Выясним, что обозначают все знаки, использованные в записи этих правил; как их применять на практике.

Рассмотрим, например, правило заключения. В нем обозначены две посылки А(х) => В(х) и А (а). Первую называют общей посылкой, это может быть теорема, определение и, вообще, предложение вида А(х) => В(х). Вторую посылку А(а) называют частной, она получается из условия А(х) при х = а. Предложение В(а) - это заключение, оно получается из В(х) при х = а. Посылки отделены от заключения чертой, которая заменяет слово «следовательно».

Приведем пример умозаключения, выполненного по правилу заключения:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 13-делится на 5.

В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х)», где А(х) - это «запись числа x оканчивается цифрой 5», а В(х) - «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей посылки при х = 135 (т.е. это А (135)). Заключение является высказыванием, полученным из В(х) при х = 135 (т.е. это 5(135)). Приведем теперь пример умозаключения, выполненного по правилу отрицания:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5.

Видим, что в этом умозаключении общая посылка такая же, как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5» (т.е. это 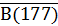). Заключение - это отрицание предложения «Запись числа 177 не оканчивается цифрой 5» (т.е. ).

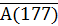И наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма.

Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.

В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где А(х) - это предложение «х кратно 12», В(х) -предложение «х кратно 6» и С(х) - предложение «х кратно 3». Заключение представляет собой высказывание «если А (х), то С(х)».

Конечно, возникает вопрос, почему умозаключения, выполненные по правилам заключения, отрицания и силлогизма, будут дедуктивными (правильными)? Дело в том, что, выполняя рассуждения по этим правилам, мы всегда будем получать истинное заключение, что и требуется в дедуктивном умозаключении. Убедиться в этом можно, если воспользоваться кругами Эйлера.

В логике существуют различные способы проверки правильности умозаключений. Мы рассмотрим тот, который предполагает использование кругов Эйлера. Сначала данное умозаключение можно записать на теоретико-множественном языке, затем посылки изобразить на кругах Эйлера, считая их истинными. После этого надо выяснить, всегда ли при таких посылках истинно заключение. Если оказывается, что всегда, то говорят, что данное умозаключение правильное, дедуктивное. Если же возможен рисунок, из которого видно, что заключение может быть ложным, то говорят, что всякое умозаключение, выполненное по такой схеме, является дедуктивным, неправильным.

Покажем, что умозаключение, выполненное по правилу заключения является дедуктивным. Сначала запишем это правило на теоретико-множественном языке.

Посылка А (х) => В(х) может быть записана в виде Т_А Ì Т_В, где Т_А и Т _В - множества истинности высказывательных форм А (х) и В(х).

Частная посылка А(а) означает, что а Î Т_А, а заключение В(а) показывает, что а Î Т_В.

Все умозаключение, построенное по правилу заключения, запишется на теоретико-множественном языке так:

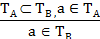
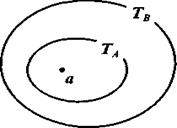
Изобразив на кругах Эйлера множества Т_А и Т_в, и обозначив элемент а Î Т_А, мы увидим, что а Î Т_В (рис. 37), т. е. а Î Т_А Þ а Î Т_В. Аналогичным образом можно проверить и другие правила дедуктивных умозаключений. Кроме того, такой способ проверки правильности умозаключений можно использовать и в тех случаях, когда умозаключение выполнено по схеме, отличной от рассмотренных.

Задача. Правильно ли следующее умозаключение: «если запись числа оканчивается цифрой 5, то число делится на 5. Число 125 делится на 5. Следовательно, запись числа 125 оканчивается цифрой 5».

Решение. Это умозаключение выполнено по схеме,

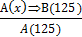
которую в общем виде можно представить так: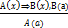

Но такой схемы среди названных выше нет. Является ли она правилом дедуктивного умозаключения?

Чтобы ответить на этот вопрос, воспользуемся кругами Эйлера. На теоретико-множественном языке полученное правило можно записать так:

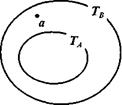(рис. 38).

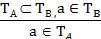
Изобразим на кругах Эйлера множества Т_А и Т_B и обозначим элемент а, принадлежащий множеству Т_В. Но оказывается, что он может содержаться в множестве Т_А, а может и не принадлежать ему (рис. 38).

В логике считают, что такая схема не является правилом дедуктивного умозаключения, так как она не гарантирует истинности заключения. И вообще при анализе умозаключения нельзя отождествлять правильность умозаключения с истинности полученного заключения: заключение может быть истинным, а само умозаключение не быть дедуктивным, правильным.

Возвращаясь к вопросу нашей задачи, скажем, что данное в ней умозаключение не является правильным, так как выполнено по схеме, не гарантирующей истинности заключения.

Как же надо действовать, чтобы установить, правильно ли умозаключение или нет? Для этого есть два пути. Первый - это показа что данное умозаключение выполнено по одному из известных правил вывода. Второй - сформулировать данное умозаключение на теоретико-множественном языке и воспользоваться кругами Эйлера так, как описано выше.

Полезно запомнить и не путать с правилом заключения такую схему:

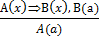
а с правилом отрицания схему:

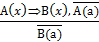
Эти схемы не гарантируют истинности заключения и, следовательно, не являются правилами дедуктивных умозаключений.

Заметим, что полное дедуктивное умозаключение по приведенным трем правилам требует указания двух посылок. Однако в процессе рассуждений эти правила иногда сокращают, опуская одну из посылок. Например, объясняя, почему 6 < 8, ученик говорит, что «6 при счете называют раньше, чем 8, значит, 6 < 8». Является ли это умозаключение дедуктивным? Если «да», то по какому правилу оно выполнено?

В объяснении ученика пропущена общая посылка: «если число а при счете называют раньше числа b, то а меньше b». Если ее восстановить, то умозаключение ученика примет вид:

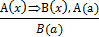
а это правило заключения.

Заметим еще, что, выполняя умозаключения, можно менять очередь посылок и можно начинать с заключения, а потом воспроизводить посылки.

Заметим также, что если общие посылки в рассмотренных правилах дедуктивных умозаключении содержат более одной переменной, то это не нарушает смысла этих правил.

Упражнения

1. В каждом из следующих умозаключений выделите посылки и заключение:

а) Если число натуральное, то оно целое; если число целое, то оно рациональное, следовательно, если число натуральное, то оно рациональное.

б) Если число натуральное, то оно целое; число 138 – натуральное, следовательно, оно целое.

в) Всякое натуральное число целое; число 138 - целое, следовательно, оно натуральное.

г) Всякое натуральное число целое; число 0,2 не является целым, следовательно, оно не является и натуральным.

2. Проанализируйте схему каждого умозаключения из упражнения 1. Есть ли среди них умозаключения, не являющиеся дедуктивными?

3. Используя правило заключения, закончите умозаключение так, чтобы оно было дедуктивным:

а) Если четырехугольник - прямоугольник, то в нем диагонали равны. Четырехугольник АВСИ...

б) Равные треугольники имеют равные площади. Треугольники АВС и КLМ...

в) Для того чтобы ромб был квадратом, достаточно, чтобы в нем был прямой угол. Ромб АВСИ.

4. Используя правило отрицания, закончите умозаключения из упражнения 3 так, чтобы они были дедуктивными.

5. Восстановите общую посылку в умозаключении:

а) Число 12 - натуральное, следовательно, оно положительное.

б) Число 15 - нечетное, следовательно, оно не делится на 2.

6. Постройте дедуктивное умозаключение, доказывающее, что

а) 130 делится на 10,

б) 137 не делится на 10.

в) Четырехугольник АВСБ - прямоугольник.

г) Четырехугольник АВСБ не является прямоугольником.

7. Используя круги Эйлера, проверьте, правильны ли следующие умозаключения:

а) Всякий квадрат является прямоугольником; четырехугольник АВСБ не квадрат, следовательно, он не является прямоугольником.

б) Некоторые прямоугольники - квадраты; все квадраты - правильные многоугольники, следовательно, некоторые прямоугольник являются правильными многоугольниками.

8. Сравнивая выражения 36-7 и 36-4, ученик рассуждал так: «36-меньше 36-4, так как 7 больше 4». Восстановите его рассуждение полностью. Назовите посылки и заключение.

Не нашли, что искали? Воспользуйтесь поиском: