
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Неравенства с одной переменной
Предложения 2 х + 7 > 10- х, х 2+7 х < 2, (х +2)(2 х -3) > 0 называют неравенствами с одной переменной.
В общем виде это понятие определяют так:
 Определение. Пусть ¦ (х) и g(х) - два выражения с переменной х и областью определения X. Тогда неравенство вида ¦ (х) > g(х) или ¦ (х) < g(х) называется неравенством с одной переменной. Множество X называется областью его определения.
Определение. Пусть ¦ (х) и g(х) - два выражения с переменной х и областью определения X. Тогда неравенство вида ¦ (х) > g(х) или ¦ (х) < g(х) называется неравенством с одной переменной. Множество X называется областью его определения.
Значение переменной х из множества X, при котором неравенство обращается в истинное числовое неравенство, называется его решением. Решить неравенство – это значит найти множество его решений.
Так, решением неравенства 2 х + 7> 10- х, х Î R является число х = 5, так как 2×5 + 7 > 10-5- истинное числовое неравенство. А множество его решений - это промежуток (1,¥), который находят, выполняя преобразование неравенства: 2 х + 7>10- х => 3 х >3 => х >1.
В основе решения неравенств с одной переменной лежит понятие Равносильности.
 Определение. Два неравенства называются равносильными, если их множества решений равны.
Определение. Два неравенства называются равносильными, если их множества решений равны.
Например, неравенства 2 х + 7> 10 и 2 х >3 равносильны, так как их 2 множества решений равны и представляют собой промежуток ( ).
).
Теоремы о равносильности неравенств и следствия из них аналогичны соответствующим теоремам о равносильности уравнений. При их доказательстве используются свойства истинных числовых неравенств.
Теорема 3. Пусть неравенство ¦(х) > g(х) задано на множестве X и h(х) - выражение, определенное на том же множестве. Тогда неравенства ¦(х) > g(х) и ¦(х) + h(х) > g(х) + h(х) равносильны на множестве X.
Из этой теоремы вытекают следствия, которые часто используются
при решении неравенств:
1) Если к обеим частям неравенства ¦ (х) > g(х) прибавить одно и то же число d, то получим неравенство ¦(х) + d > g(х) + d, равносильное исходному.
2) Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Теорема 4. Пусть неравенство ¦(х) > g(х) задано на множестве X и h(х) - выражение, определенное на том же множестве, и для всех х из множества X выражение h(х) принимает положительные значения. Тогда неравенства ¦(х) > g(х) и ¦(х)- h (х) > g(х)× h (х) равносильны на множестве X..
Из этой теоремы вытекает следствие: если обе части неравенства ¦(х) > g(х) умножить на одно и то же положительное число d, то получим неравенство ¦(х)× d > g(х)×d, равносильное данному.
Теорема 5; Пусть неравенство ¦(х) > g(х) задано на множестве X и h(х) - выражение, определенное на том же множестве, и для всех х их множества X выражение h (х) принимает отрицательные значения. Тогда неравенства ¦(х) > g(х) и ¦(х)× h (х) < g(х)×h(х) равносильны на множестве X.
Из этой теоремы вытекает следствие: если обе части неравенства ¦(х) > g(х) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство ¦(х) < g(х)×d, равносильное данному.
Решим неравенство 5 х - 5 < 2 х - 16, х Î R, и обоснуем все преобразования, которые мы будем выполнять в процессе решения.
| Преобразования | Обоснование преобразований |
| 1.Перенесем выражение 2 х в левую часть, а число -5 в правую, поменяв их знаки на противоположные: 5 х -2 х < 16 + 5 | Воспользовались следствием 2 из теоремы 3, получили неравенство, равносильное исходному. |
| 2. Приведем подобные члены в левой и правой частях неравенства: 3 х < 21. | Выполнили тождественные преобразования выражений в левой и правой частях неравенства - они не нарушили равносильности неравенств: данного и исходного. |
| 3. Разделим обе части неравенства на 3: х < 21. | Воспользовались следствием из теоремы 4, получили неравенство, равносильное исходному. |
Решением неравенства х < 7 является промежуток (-¥, 7) и, следовательно, множеством решений неравенства 5 х - 5 < 2 х + 16 является промежуток (-¥, 7).
Упражнения
1. Установите, какие из следующих записей являются неравенствами с одной переменной:
а)-12-7 х <3 х + 8; г) 12 х + 3(х -2);
б)15(х + 2)>4; д) 17-12×8;
в) 17(13 + 8) < 14-9; е) 2 х 2 + 3 х -4 > 0.
2. Является ли число 3 решением неравенства 6(2 х + 7) < 15(х + 2), х Î R? А число 4,25?
3. Равносильны ли на множестве действительных чисел следующие пары неравенств:
а)-17 x<- 51 и x >3;
б) 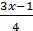 >0 и 3 x -1>0;
>0 и 3 x -1>0;
в)6-5 х >-4 и х <2?
4. Какие из следующих высказываний истинны:
а)-7 x <-28 => х >4;
б) х < 6 => х < 5;
в) х < 6 => х < 20?
5. Решите неравенство 3(х - 2) - 4(х + 1) < 2(х - 3) - 2 и обоснуйте все преобразования, которые будете при этом выполнять.
6. Докажите, что решением неравенства 2(х + 1) + 5 > 3 - (1 - 2 х) является любое действительное число.
7. Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3(2 - х) - 2 > 5 - 3 х.
8. Одна сторона треугольника равна 5 см, а другая 8 см. Какой Может быть длина третьей стороны, если периметр треугольника:
а) меньше 22 см;
б) больше 17 см?
Глава III. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
Для школьной математики натуральное число является тем понятием, с которого, как правило, начинается обучение. И уже в начальных классах учащиеся знакомятся с различными функциями натурального числа. Отвечая на вопрос: «Сколько машин изображено на рисунке?», - они имеют дело с числом как количественной характеристикой множества предметов. Производя счет предметов, используют натуральное число как характеристику порядка. В задачах, связанных с измерением величин, число выступает как значение величины при выбранной единице, т. е. как мера величины. Большое внимание уделяется в начальном курсе математики и еще одной роли числа - как компоненту вычислений. Таким образом, натуральное число имеет много функций, и многие из них должны быть поняты и усвоены уже младшими школьниками. Поэтому важной задачей учителя является овладение теми теориями, в которых обосновываются различные подходы к определению натурального числа и действий над числами.
В нашем курсе мы рассмотрим аксиоматическое определение системы натуральных чисел, отвечающее на вопрос, что представляет собой число как элемент натурального ряда; затем построим ее теоретико-множественную модель и выясним, что представляет собой натуральное число как мера величины, и, наконец, изучим способы записи чисел и алгоритмы действий над ними.
Не нашли, что искали? Воспользуйтесь поиском: