Понятие преобразования

Главной задачей геометрии является обоснование правил построения фигур с заданными свойствами. Но при построении используется понятие равенства фигур, определить которое можно через понятие преобразования.

Пусть задана некоторая фигура F и каждой точке фигуры F поставлена в соответствие единственная точка плоскости. Множество точек, сопоставленных точкам фигуры F, является некоторой фигурой F, вообще говоря, отличной от F. Говорят, что фигура F' получена преобразованием фигуры F. Можно сказать также, что фигура F' является образом фигуры F для данного преобразования, а фигура F - прообразом фигуры F'.

Если А' - точка фигуры А', соответствующая точке А фигуры Р, то говорят, что А' - образ точки А, а точка А - прообраз точки А'.

Преобразования, изучаемые в геометрии, как правило, являются взаимно однозначными, т.е. такими, при которых разным точкам фи­гуры соответствуют разные образы. Простейший случай взаимно одно­значного преобразования - это преобразование, при котором каждой точке А фигуры вставится в соответствие эта же точка, т.е. образом фигуры ^является сама эта фигура. Такое преобразование называется тождественным преобразованием.

Рассмотрим примеры преобразований фигур.

1. Симметрия относительно точки (центральная симметрия).

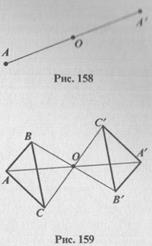Пусть О - фиксированная точка и А - произвольная точка плоскости. Точка А' называется симметричной точке А относительно точки О, если точки А, О, А' лежат на одной прямой и О А = О А' (рис. 158). Точка, симметричная точке О, есть сама эта точка.

Пусть Р - данная фигура и О - фиксированная точка плоскости. Преобразование фигуры Р в фигуру Р', при котором каждая точка А фигуры Р переходит в точку А' фигуры Р', симметричную А относительно точки О, называется преобразованием симметрии относительно точки О. На ри­сунке 159 выполнено преобразование треугольника АВС в симметричный ему относительно точки О треугольник А'В'С'.

Если преобразование симметрии относительно точки О переводит фигуру в себя, то фигура называется центрально симметричной, а точка О - ее центром симметрии.

Например, центрально симметричными являются параллелограмм (центром симметрии в нем является точка пересечения диагоналей), окружность с центром в точке О.

2. Симметрия относительно прямой (осевая симметрия).

Пусть р - фиксированная прямая. Тогда А' называется симметричной точке А относительно прямой р, если прямая АА' перпендикулярна прямой р и ОА' = ОА, где О - точка пересечения прямых АА' и р (рис. 160).

Если точка А лежит на прямой p, то симметричная ей точка есть сама точка А. Точка, симметричная точке А', есть точка А.

Пусть F -данная фигура и р - фиксированная прямая. Преобразование фигуры F в фигуру F', при котором каждая точка А фигуры F переходит в точку А' фигуры F', симметрично относительно прямой р, называется преобразованием симметрии отно­сительно прямой р. При этом фигуры F и F' называются симметричными относительно прямой р. На рисунке 161 изображены треугольники АВС и А'В'С', симметричные относительно прямой р.

Если преобразование симметрии относительно прямой р переводит фигуру F всебя, то фигура называется симметричной относительно прямой р, прямая р называется осью симметрии фигуры. Например, осями симметрии прямоугольника являются прямые, проходящие через точку пересечения его диагоналей параллельно сторонам.

3. Гомотетия. Пусть F - данная фигура и О - фиксированная точка (рис. 162). Проведем через произвольную точку X фигуры F луч ОХ и отложим на нем отрезок ОХ' равный k-ОХ, где k - положительное число. Преобразование фигуры F, при котором каждая ее точка X переходит в такую точку X', что ОХ' = k×ОХ, называется гомотетией относительно центра О. Число k называется коэффициентом гомотетии. Фигуры F и F называются гомотетичными.

На рисунке 162 четырехугольник А'В'С'О' гомотетичен четырехугольнику АВСБ. Центр гомотетии - точка О, а ее коэффициент равен 2.

Упражнения

1. Постройте на листе бумаги точку О и четырехугольник F. С помощью циркуля и линейки постройте фигуру F', симметричную данной относительно точки О.

2. Назовите три фигуры, имеющие центр симметрии. Сколько центров симметрии имеет: а) отрезок; б) квадрат?

3.Существуют ли фигуры, не имеющие центра симметрии?

4. Изобразите на листе бумаги прямую р и многоугольник F. С помощью циркуля и линейки постройте фигуру F', симметричную данной относительно прямой р.

5. Возьмите лист бумаги, проведите на нем прямую р и отметьте какую-нибудь точку А, не лежащую на этой прямой. Перегните лист бумаги по линии р, отметьте точку А', с которой совместится точка А, и снова разогните его. Докажите, что полученная точка А' и данная точка А симметричны относительно прямой p.

Верно ли обратное утверждение, т. е. совместятся ли точки А и А, симметричные относительно прямой р, при перегибании чертежа по этой прямой?

6. Назовите три фигуры, имеющие ось симметрии. Сколько осей
имеет: а) отрезок; б) квадрат; в) равносторонний треугольник?

7. Существуют ли фигуры, не имеющие оси симметрии?

8. На листе бумаги постройте прямоугольник и ромб. Перегните лист и найдите все оси симметрии данных фигур. Как аналогичным способом найти оси симметрии и центр окружности?

9. На листе бумаги изобразите точки А, В и С. Не используя чертежных инструментов, путем перегибания этого листа найдите: а) центр описанной около треугольника АВС окружности; б) центр вписанной в треугольник А ВС окружности.

10. На листе бумаги отмечены точки А и В. С помощью перегибания листа изобразите квадрат АВСD.

Не нашли, что искали? Воспользуйтесь поиском: