Системи лінійних рівнянь

Рівняння виду (1) називається лінійним рівнянням з n невідомими: . Слово лінійне означає, що рівняння 1-го степеня.

Розв’язком такого рівняння буде такий упорядкований набір чисел 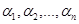, який перетворює наше рівняння в числову тотожність.

Рівняння виду (1) можна використати для побудови системи рівнянь:

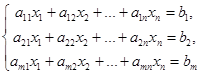(2)

Система (2) називається системою m лінійних рівнянь з n невідомими.

Якщо кількість рівнянь даної системи (m) не дорівнює кількості невідомих (n), то таку систему називають прямокутною системою.

Якщо m=n, то система називається квадратною.

Розв’язком системи (2) будемо називати такий набір чисел 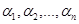, який задовольняє кожне рівняння системи (2). Це буде перетин множин розв’язків кожного рівняння даної системи.

Якщо система (2) має принаймні один розв’язок, то така система називається сумісною.

Якщо ж система (2) зовсім не має розв’язків, то система називається несумісною.

Якщо система (2) має точно один розв’язок, то така система називається визначеною.

Якщо система (2) має більше, ніж один розв’язок, то вона називається невизначеною.

Крім того в системі (2) всі вільні члени можуть бути рівні 0. Тоді система має такий вид:

(3)

Системи виду (3) називається однорідними.

Однорідна система завжди сумісна, тому що вона завжди має принаймні один розв’язок – нульовий .

Нехай задана система 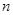лінійних рівнянь з 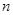невідомими 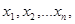коефіцієнтами при яких є елементами матриці А, а вільними членами є числа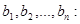

(4)

Якщо визначник системи (4), тобто визначник, що складається з коефіцієнтів при невідомих

, (5)

то система (4) має єдиний розв’язок. Цей розв’язок можна знайти різними способами. Розглянемо два з них.

І. Метод Крамера. Позначимо через визначник, що утворюється з (5) після заміни його першого стовпчика стовпчиком вільних членів системи (4). аналогічно позначимо через визначник, що утворюється з (5) після заміни його другого стовпчика стовпчиком вільних членів системи (4), …, - замінено останній стовпчик стовпчиком вільних членів.

Тоді розв’язок системи (4) записується у вигляді:

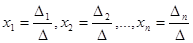. (6)

Формули (1.7) називаються формулами Крамера. Якшо , а хоча б один з , , …., відмінний від нуля, то система (4) розв’язків немає. Якщо ж = =…= =0, то система (4) має безліч розв’язків.

ІІ. Матричний спосіб. Якщо позначити

, - матриці-стовпчики невідомих та вільних членів, то систему (4) можна записати в матричній формі так: (7) Використовуючи властивості оберненої матриці, маємо:

(8)

З формули (8) випливає твердження: щоб знайти розв’язок системи (4), потрібно знайти обернену матрицю (це можливо, бо ), а потім помножити на матрицю В. Результат цієї дії і дає розв’язок системи (4), записаної у вигляді (8).

Приклад 1. Розв’язати задану систему рівнянь методом Крамера та за допомогою матричного методу.

Розв’язок.

І. Метод Крамера. Знаходимо визначник системи , розкладаючи його за елементами першого рядка:

ІІ. Матричний спосіб. Матриця А з коефіцієнтів при невідомих для заданої системи рівнянь має

Не нашли, что искали? Воспользуйтесь поиском: