Геометрические приложения определенного интеграла

Вычисление площади в декартовых координатах

Если функция непрерывна на [ a, b ] и положительна, то площадь криволинейной трапеции, ограниченной функцией , двумя прямыми и и отрезком [ a, b ] оси абсцисс, вычисляется по формуле

если на отрезке [ a, b ], то,

Площадь фигуры, ограниченной двумя непрерывными функциям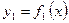и и и двумя прямыми и , где на отрезке [ a, b ], находится по формуле:

Вычисление площадей с помощью определенного интеграла осуществляется в следующим порядке:

1) делается рисунок фигуры, площадь которой необходимо найти;

2) находятся пределы интегрирования;

3) подбирается нужная формула;

4) вычисляется значение площади.

Пример 8.11. Вычислить площадь фигуры, ограниченной параболой прямыми и осью абсцисс.

Решение. Построим криволинейную трапецию

Пределы интегрирования:

Площадь вычисляем по формуле

Получаем

(кв. ед.).

Пример 8.12. Вычислить площадь фигуры, ограниченной параболой осями координат и прямой

Решение. На рисунке 2. изображена фигура, площадь которой надо найти.

Функция на отрезке [0, 2] меняет знак. Следовательно, промежуток интегрирования [0, 2] необходимо разбить на два промежутка: и . Получим:

(кв. ед).

Пример 8.13. Вычислить площадь фигуры, ограниченной параболой и прямой

Решение. Сделаем рисунок плоской фигуры, заключенной между параболой и прямой (рисунок 3).

Найдем пределы интегрирования, для этого решим систему уравнений и получим

Следовательно, пределы интегрирования:

Вычислим площадь:

(кв. ед.).

Вычисление объема тел вращения

Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой 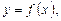осью абсцисс и двумя прямыми и находится по формуле

Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции, ограниченной непрерывной кривой 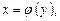осью ординат и двумя прямыми и находится по формуле

Пример 8.14 Вычислить объем тела, ограниченного поверхностью вращения параболы вокруг оси Ох и плоскостью

Решение. Найдем V_x согласно приведенной выше формуле:

(куб. ед.).

Пример 8.15. Найти объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривой и отрезком оси ординат.

Решение. Записав уравнение данной кривой в виде и используя формулу вычисления объема, получим

(куб. ед.).

Вычисление длины дуги кривой в прямоугольных координатах

Если производная функции является непрерывной функцией на отрезке [ a, b ], то длина дуги кривой , заключенная между точками с абсциссами и , находится по формуле

Пример 8.16. Найти длину дуги цепной линии между прямыми и

Решение. Найдем производную функции :

и вычислим длину дуги кривой:

Вычисление площади поверхности тела вращения

Если производная функции является непрерывной функцией, то кривая называется гладкой кривой. Площадь поверхности, образованной вращением вокруг оси Ох дуги гладкой кривой между точками с абсциссами и , вычисляется по формуле

Пример 17. Найти площадь поверхности вращения вокруг оси Ох дуги кубической параболы 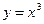при

Решение. Используем приведенную выше формулу для вычисления площади:

Вычислим этот интеграл методом подстановки. Обозначим тогда Пересчитаем пределы интегрирования: при при Получаем

(кв.ед.).

Не нашли, что искали? Воспользуйтесь поиском: