
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод Гаусса для решения систем линейных уравнений
Метод Гаусса является универсальным методом решения систем линейных уравнений. Он заключается в приведении системы к треугольному виду путем последовательного исключения неизвестных и реализуется в несколько этапов:
I этап – выбирается первое ведущее уравнение, содержащее  , и с его помощью из всех остальных уравнений исключается
, и с его помощью из всех остальных уравнений исключается  .
.
II этап – первое ведущее уравнение остается неизменным; выбирается второе ведущее уравнение из всех оставшихся и с его помощью исключается неизвестная  ;
;
III этап – первое и второе ведущие уравнения остаются неизменными. Выбирается третье ведущее и с его помощью исключается  и т.д.
и т.д.
Когда система приведена к треугольному виду, то, двигаясь в обратном порядке, находят значения неизвестных величин.
Пример 10. Решить систему методом Гаусса.

В качестве первого ведущего выбираем второе уравнение, т.к. у него первый коэффициент равен единице.

 І этап
І этап 
 ІI этап
ІI этап 
Из третьего уравнения определяем:  ; из второго:
; из второго:  ,
,  ,
,  ; из первого:
; из первого:  . Таким образом,
. Таким образом,  .
.
Замечание. Очень удобной модификацией метода Гаусса является правило прямоугольника, которое тоже реализуется поэтапно.
Пример 11. Рассмотрим систему и решим ее модифицированным методом Гаусса.
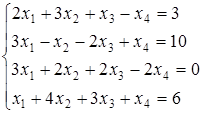
Идея подхода прежняя – расширенная матрица приводится к треугольному виду. Она составляется с участием правой части системы  и контрольного столбца
и контрольного столбца  :
:

Элементы контрольного столбца равны сумме всех элементов соответствующих строк.
I этап. Считаем первый диагональный элемент не равным нулю (в противном случае поменяет местами строки). Этот элемент назовем первым генеральным элементом. В данном случае – это число 2. Далее первую строку переписываем без изменения, а первый столбец дополняем нулями. Остальные элементы определяем по правилу прямоугольника. Чтобы построить прямоугольник, каждый элемент соединяют с первой строкой и первым столбцом, а затем – с генеральным элементом. Вычисления проводят так: из произведения элементов диагонали, содержащей генеральный элемент, вычитают произведение элементов второй диагонали. В результате указанных преобразований получим:

Контрольный столбец, вычисленный по правилу прямоугольника, по-прежнему должен равняться сумме элементов строки.
II этап. Вторым генеральным элементом будет второй диагональный элемент. Далее первую и вторую строки переписываем без изменения, а первый и второй столбец дополняем нулями. Остальные элементы находим по правилу прямоугольника.

Сократим третью строку на 2, а четвертую – на (– 2).

III этап. Выбираем третий генеральный элемент – он третий по диагонали. Три строки оставляем без изменения, три столбца дополняем нулями, остальные элементы – по правилу прямоугольника.

Матрица приведена к треугольному виду. Контрольный момент проверен. Начиная с последней строки, определим неизвестные.
 ,
,  ,
, 
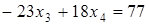 ,
,  ,
, 
 ,
,  ,
, 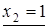
 ,
,  ,
,  .
.
Проверка:

Вопросы совместимости линейных уравнений
Ранг матрицы
Не нашли, что искали? Воспользуйтесь поиском: