| 39.Уравнение плоскости в отрезках на осях
Если плоскость пересекает оси координат в точках А(а,0,0), В(0,в,0), С(0,0,с) (а,в,с не равны 0), то ее можно представить в виде х/а+у/в+z/с=1
| 40.Векторное произведение векторов и его свойства
Векторным произведением геометрических векторов a и b называется вектор c = [a, b], который определяются следующим образом:
1) |c| = |[a, b]|;= |a|·|b|·sinφ;
2) вектор c ортогонален вектору a и вектору b;
3) векторы a, b и c образуют правую тройку векторов.
Легко видеть, что длина векторного произведения равна площади параллелограмма, построенного на векторах-сомножителях как на сторонах.
 Если векторы a и b заданы своими координатами в ортонормированном базисе e1, e2, e3:
a = (α1, α2, α3), b = (β1, β2, β3),
то координаты вектороного произведения вычисляются по формуле:
[a, b] = (α2·β3 − α3·β2, α3·β1 − α1·β3,α1·β2 − α2·β1).
То есть, если
a = α1·e1 + α2·e2 + α3·e3 и b = β1·e1 + β2·e2 +β3·e3,
то
[a, b] = (α2·β3 − α3·β2)·e1 + (α3·β1 − α1·β3)·e2 + (α1·β2 − α2·β1)·e3.
Свойства векторного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β саправедливо:
• [a, b] = −[b, a];
• [a + b, c] = [ a,c] + [b,c];
• [α·a, b] = α·[a, b];
• [a, b] = 0 тогда и только тогда, когда векторы a и b коллинеарны, (векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны);
•площадь параллелограмма, построенного на векторах a и b как на сторонах, равна длине векторного произведения векторов a и b.
Если векторы a и b заданы своими координатами в ортонормированном базисе e1, e2, e3:
a = (α1, α2, α3), b = (β1, β2, β3),
то координаты вектороного произведения вычисляются по формуле:
[a, b] = (α2·β3 − α3·β2, α3·β1 − α1·β3,α1·β2 − α2·β1).
То есть, если
a = α1·e1 + α2·e2 + α3·e3 и b = β1·e1 + β2·e2 +β3·e3,
то
[a, b] = (α2·β3 − α3·β2)·e1 + (α3·β1 − α1·β3)·e2 + (α1·β2 − α2·β1)·e3.
Свойства векторного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β саправедливо:
• [a, b] = −[b, a];
• [a + b, c] = [ a,c] + [b,c];
• [α·a, b] = α·[a, b];
• [a, b] = 0 тогда и только тогда, когда векторы a и b коллинеарны, (векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны);
•площадь параллелограмма, построенного на векторах a и b как на сторонах, равна длине векторного произведения векторов a и b.
| 41.Смешанное произведение векторов и его свойства
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где
a={ax,ay,az}
b={bx,by,bz}
c={cx,cy,cz}
Св-ва: 1. При перестановке 2х сомножителей:
a*b*c=-b*c*a
2. не меняется при перестановке циклических сомножителей:
a*b*c=c*a*b=b*c*a
3.а) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0
б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах
если a*b*c>0, то тройка a,b,c - правая
если a*b*c<0, то тройка a,b,c – левая 
| 42.Условия параллельности и перпендикулярности плоскостей
 N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
 1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
 A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
|
 43.Каноническое уравнение прямой
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены точка M0(x0 y0, z0) и вектор a = (l, m, n).
Прямая, проходящая через точку M0(x0 y0, z0), параллельно вектору a = (l, m, n), описывается в этой системе координат уравнениями 43.Каноническое уравнение прямой
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены точка M0(x0 y0, z0) и вектор a = (l, m, n).
Прямая, проходящая через точку M0(x0 y0, z0), параллельно вектору a = (l, m, n), описывается в этой системе координат уравнениями
 Эти уравнения называются каноническими уравнениями прямой.
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
Эти уравнения называются каноническими уравнениями прямой.
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
 Эти уравнения называются каноническими уравнениями прямой, проходящей через две заданные точки.
Эти уравнения называются каноническими уравнениями прямой, проходящей через две заданные точки.
 Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S

| 44.Параметрические уравнения прямой в пространстве
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены точка M0(x0 y0, z0) и вектор a = (l, m, n).
Прямая, проходящая через точку M0(x0 y0, z0), параллельно вектору a = (l, m, n), описывается в этой системе координат уравнениями
 Эти уравнения называются параметрическими уравнениями прямой.
Пусть в трехмерном пространствев некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
Эти уравнения называются параметрическими уравнениями прямой.
Пусть в трехмерном пространствев некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
 Эти уравнения называются параметрическими уравнениями прямой, проходящей через две заданные точки.
Эти уравнения называются параметрическими уравнениями прямой, проходящей через две заданные точки.

| 45.Уравнение прямой в пространстве, проходящее через две заданные точки
Если на прямой в пространстве отметить две произвольные точки M1(x1, y1, z1) и M2(x2, y2, z2), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
 .
Кроме того, для точки М1 можно записать: .
Кроме того, для точки М1 можно записать:
 .
Решая совместно эти уравнения, получим: .
Решая совместно эти уравнения, получим:
 .
Это уравнение прямой, проходящей через две точки в пространстве .
Это уравнение прямой, проходящей через две точки в пространстве
|
|

 Если векторы a и b заданы своими координатами в ортонормированном базисе e1, e2, e3:
a = (α1, α2, α3), b = (β1, β2, β3),
то координаты вектороного произведения вычисляются по формуле:
[a, b] = (α2·β3 − α3·β2, α3·β1 − α1·β3,α1·β2 − α2·β1).
То есть, если
a = α1·e1 + α2·e2 + α3·e3 и b = β1·e1 + β2·e2 +β3·e3,
то
[a, b] = (α2·β3 − α3·β2)·e1 + (α3·β1 − α1·β3)·e2 + (α1·β2 − α2·β1)·e3.
Свойства векторного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β саправедливо:
• [a, b] = −[b, a];
• [a + b, c] = [ a,c] + [b,c];
• [α·a, b] = α·[a, b];
• [a, b] = 0 тогда и только тогда, когда векторы a и b коллинеарны, (векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны);
•площадь параллелограмма, построенного на векторах a и b как на сторонах, равна длине векторного произведения векторов a и b.
Если векторы a и b заданы своими координатами в ортонормированном базисе e1, e2, e3:
a = (α1, α2, α3), b = (β1, β2, β3),
то координаты вектороного произведения вычисляются по формуле:
[a, b] = (α2·β3 − α3·β2, α3·β1 − α1·β3,α1·β2 − α2·β1).
То есть, если
a = α1·e1 + α2·e2 + α3·e3 и b = β1·e1 + β2·e2 +β3·e3,
то
[a, b] = (α2·β3 − α3·β2)·e1 + (α3·β1 − α1·β3)·e2 + (α1·β2 − α2·β1)·e3.
Свойства векторного произведения геометрических векторов
Для любых векторов a, b и c и любых чисел α, β саправедливо:
• [a, b] = −[b, a];
• [a + b, c] = [ a,c] + [b,c];
• [α·a, b] = α·[a, b];
• [a, b] = 0 тогда и только тогда, когда векторы a и b коллинеарны, (векторное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны);
•площадь параллелограмма, построенного на векторах a и b как на сторонах, равна длине векторного произведения векторов a и b.

 N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
 1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
 A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
 43.Каноническое уравнение прямой
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены точка M0(x0 y0, z0) и вектор a = (l, m, n).
Прямая, проходящая через точку M0(x0 y0, z0), параллельно вектору a = (l, m, n), описывается в этой системе координат уравнениями
43.Каноническое уравнение прямой
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены точка M0(x0 y0, z0) и вектор a = (l, m, n).
Прямая, проходящая через точку M0(x0 y0, z0), параллельно вектору a = (l, m, n), описывается в этой системе координат уравнениями
 Эти уравнения называются каноническими уравнениями прямой.
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
Эти уравнения называются каноническими уравнениями прямой.
Пусть в трехмерном пространстве в некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
 Эти уравнения называются каноническими уравнениями прямой, проходящей через две заданные точки.
Эти уравнения называются каноническими уравнениями прямой, проходящей через две заданные точки.
 Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S

 Эти уравнения называются параметрическими уравнениями прямой.
Пусть в трехмерном пространствев некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
Эти уравнения называются параметрическими уравнениями прямой.
Пусть в трехмерном пространствев некоторой декартовой системе координат определены две точки M0(x0 y0, z0) и M1(x1 y1, z1).
Прямая, проходящая через точки M(x0 y0, z0) и M1(x1 y1, z1), описывается в этой системе координат уравнениями
 Эти уравнения называются параметрическими уравнениями прямой, проходящей через две заданные точки.
Эти уравнения называются параметрическими уравнениями прямой, проходящей через две заданные точки.

 .
Кроме того, для точки М1 можно записать:
.
Кроме того, для точки М1 можно записать:
 .
Решая совместно эти уравнения, получим:
.
Решая совместно эти уравнения, получим:
 .
Это уравнение прямой, проходящей через две точки в пространстве
.
Это уравнение прямой, проходящей через две точки в пространстве
 - функция
- функция

 - коэффициенты квадратичной формы. Без ограничения общности считают
- коэффициенты квадратичной формы. Без ограничения общности считают  тогда
тогда
 Если переменные
Если переменные  принимают действительные значения и
принимают действительные значения и  квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица
квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица  называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если  Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве
Главные миноры матрицы A называются главными минорами квадратичной формы. В пространстве  квадратичную форму можно записать в виде
квадратичную форму можно записать в виде  где X - координатный столбец вектора
где X - координатный столбец вектора  В пространстве
В пространстве 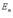 квадаратичную форму можно представить в виде
квадаратичную форму можно представить в виде  где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
Положительно-определенные: Квадратичные формы, для которых
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
Положительно-определенные: Квадратичные формы, для которых  таких, что
таких, что  Нормальный вид
Нормальный вид  Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны
Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны  (критерий Сильвестра).
Отрицательно-определенные: Квадратичные формы, для которых
(критерий Сильвестра).
Отрицательно-определенные: Квадратичные формы, для которых  таких, что
таких, что  Квадратичная форма является отрицательно-определенной тогда и только тогда, когда
Квадратичная форма является отрицательно-определенной тогда и только тогда, когда  Положительно-полуопределенные:Квадратичные формы, для которых
Положительно-полуопределенные:Квадратичные формы, для которых  таких, что
таких, что 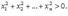 Нормальный вид
Нормальный вид  r < n, r = rank A.
Отрицательно-полуопределенные: Квадратичные формы, для которых
r < n, r = rank A.
Отрицательно-полуопределенные: Квадратичные формы, для которых  таких, что
таких, что  Нормальный вид
Нормальный вид  r < n, r = rank A.
Неопределенные: Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид:
r < n, r = rank A.
Неопределенные: Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид:  r = rank A.
r = rank A.