Теоретический материал. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О₁ есть геометрическое место всех точек пространства, находящихся от точки O ₁ на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками простран­ства и тройками чисел х, у и z — их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего ко­ординаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменны­ми х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называ­ются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M₁(x₁;y₁;z₁) на данной поверхности, достаточно подставить координаты точки M₁ в уравнение поверхности вместо пере­менных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют — не лежит.

Зачем переводят геометрические понятия на язык координат и векторов?

Это делается для того, чтобы построить вычислительные алгоритмы для решения геометрических задач. Основной для этого является уравнения различных фигур в пространстве и, прежде всего, уравнения плоскости и сферы (поверхности шара).

1. Уравнение плоскости.

Плоскость можно задать одной содержащейся в ней точкой и вектором n,перпендикулярным этой плоскости (его называют вектором нормали к плоскости). Необходимым и достаточным условием того, что точка P(x;y;z) принадлежит плоскости, является следующее: ┴ n или в виде равенства: . Задав координаты нормали n(A;B;C), получим уравнение плоскости в координатной форме:

2. Уравнение сферы.

Точка P(x;y;z) находится на сфере с центром C(a;b;c) и радиусом R, если выполнено условие . Это условие легко переписать в координатах:

.

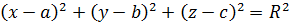Данное уравнение обобщает уравнение окружности и плоскости.

Решение примеров и задач (алгоритм выполнения задания):

Пример 1: Принадлежат ли точки и плоскости, общее уравнение которой имеет вид .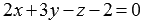

Решение: Подставим координаты точки М₀ в общее уравнение плоскости: 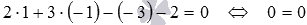. В результате приходим к верному равенству, следовательно, точка лежит в плоскости.

Проделаем такую же процедуру с координатами точки N₀: 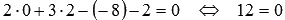. Получаем неверное равенство, поэтому, точка не лежит в плоскости, определенной общим уравнением плоскости .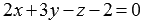

Ответ: М₀ лежит в плоскости, а N₀ – не лежит.

Пример2: Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости . Запишите координаты всех нормальных векторов этой плоскости.

Решение: Нам известно, что коэффициенты при переменных x, y и z в общем уравнении плоскости являются соответствующими координатами нормального вектора этой плоскости. Следовательно, нормальный вектор заданной плоскости имеет координаты . Множество всех нормальных векторов можно задать как .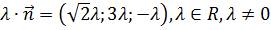

Ответ: .

Теперь рассмотрим обратную задачу – задачу составления уравнения плоскости, когда известны координаты ее нормального вектора. Очевидно, что существует бесконечно много параллельных плоскостей, нормальным вектором которых является вектор . Поэтому, зададим дополнительное условие, чтобы обозначить одну конкретную плоскость. Будем считать, что точка принадлежит плоскости. Таким образом, задав нормальный вектор и точку плоскости , мы зафиксировали плоскость. Получим общее уравнение этой плоскости.

Общее уравнение плоскости с нормальным вектором имеет вид . Так как точка лежит на плоскости, то ее координаты удовлетворяют уравнению плоскости, следовательно, справедливо равенство . Вычтем из левой и правой части равенства левую и правую части равенства соответственно. При этом получаем уравнение вида 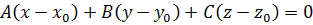, которое является общим уравнением плоскости, проходящей через точку и имеющей направляющий вектор плоскости .

Это уравнение можно было получить и иначе.

Очевидно, что множество точек трехмерного пространства определяют требуемую плоскость тогда и только тогда, когда векторы и перпендикулярны. То есть, тогда и только тогда, когда их скалярное произведение равно нулю: .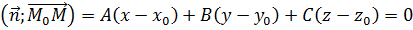

Пример 3: Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку 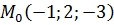, а - нормальный вектор этой плоскости.

Решение:

Приведем два решения этой задачи.

Из условия имеем . Подставляем эти данные в общее уравнение плоскости 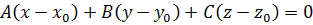, проходящей через точку :

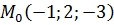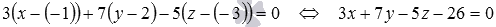
Теперь второй вариант решения.

Пусть - текущая точка плоскости. Находим координаты вектора по координатам точек начала и конца: . Для получения требуемого общего уравнения плоскости осталось только воспользоваться необходимым и достаточным условием перпендикулярности векторов и :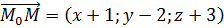

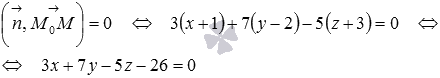
Ответ: .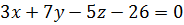

Решите примеры:

Пример 1: Принадлежат ли точки 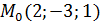и плоскости, общее уравнение которой имеет вид .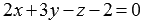

Пример 2: Плоскость в прямоугольной системе координат Oxyz задана общим уравнением плоскости 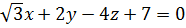. Запишите координаты всех нормальных векторов этой плоскости.

Пример 3: Напишите уравнение плоскости, если в прямоугольной системе координат Oxyz в пространстве она проходит через точку , а - нормальный вектор этой плоскости.

Вопросы для самоконтроля:

1. Как записывается уравнение прямой?

2. Запишите уравнение плоскости?

3. Запишите уравнение сферы?

4. Что такое «нормаль плоскости»?

Рекомендуемая литература:

Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.

10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.

11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.

12. Пехлецкий И.Д. Математика: учебник. – М., 2003.

13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. Математика для колледжей» Математический Портал – библиотека math-portal.ru
Тема 6. Основы тригонометрии.

Не нашли, что искали? Воспользуйтесь поиском: